ODEINT 求解常微分方程(4）

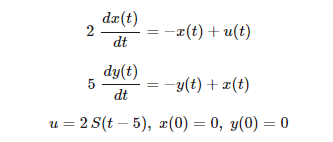
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

# function that returns dz/dt
def model(z,t,u):
    x = z[0]
    y = z[1]
    dxdt = (-x + u)/2.0
    dydt = (-y + x)/5.0
    dzdt = [dxdt,dydt]
    return dzdt

# initial condition
z0 = [0,0]

# number of time points
n = 401

# time points
t = np.linspace(0,40,n)

# step input
u = np.zeros(n)
# change to 2.0 at time = 5.0
u[51:] = 2.0

# store solution
x = np.empty_like(t)
y = np.empty_like(t)
# record initial conditions
x[0] = z0[0]
y[0] = z0[1]

# solve ODE
for i in range(1,n):
    # span for next time step
    tspan = [t[i-1],t[i]]
    # solve for next step
    z = odeint(model,z0,tspan,args=(u[i],))
    # store solution for plotting
    x[i] = z[1][0]
    y[i] = z[1][1]
    # next initial condition
    z0 = z[1]

# plot results
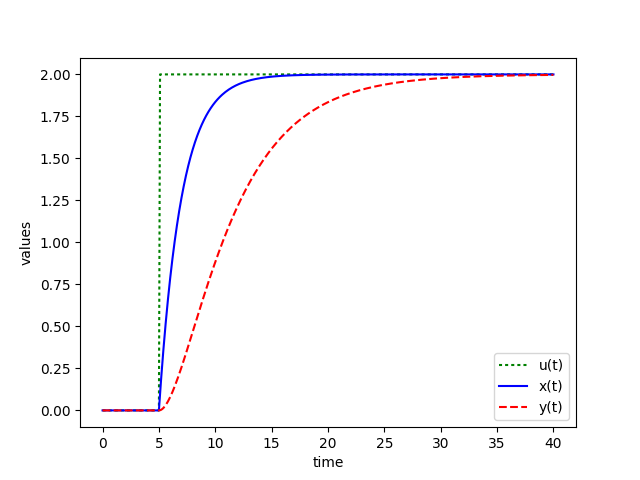
plt.plot(t,u,'g:',label='u(t)')
plt.plot(t,x,'b-',label='x(t)')
plt.plot(t,y,'r--',label='y(t)')
plt.ylabel('values')
plt.xlabel('time')
plt.legend(loc='best')
plt.show()