【分类问题中模型的性能度量(一)】错误率、精度、查准率、查全率、F1详细讲解

文章目录

• 1.错误率与精度
• 2.查准率、查全率与F1
• 2.1 查准率、查全率
• 2.2 P-R曲线(P、R到F1的思维过渡)
• 2.3 F1度量
• 2.4 扩展

性能度量是用来衡量模型泛化能力的评价标准，错误率、精度、查准率、查全率、F1、ROC与AUC这7个指标都是分类问题中用来衡量模型泛化能力的评价标准，也就是性能度量。本文主要介绍前五种度量，ROC与AUC讲解见超强整理，超详细解析，一文彻底搞懂ROC、AOC。

性能度量反映了任务需求，在对比不同模型的能力时，使用不同的性能度量往往会导致不同的评判结果；这就意味着模型的“好坏”是相对的，什么样的模型是好的，不仅取决于算法和数据，还决定于任务需求。

1.错误率与精度

错误率与精度是最好理解，也是分类任务中最常用的两种性能度量，既适用于二分类任务，也适用于多分类任务。

• 错误率(error rate)：分类错误的样本数占样本总数的比例，也就是：
  
  E=am(其中，a为分类错误的样本数，m为样本总数)E = \frac{a}{m}(其中，a为分类错误的样本数，m为样本总数)E=ma​(其中，a为分类错误的样本数，m为样本总数)
• 精度(accuracy)：分类正确的样本数占样本总数的比例，也就是：
  
  精度=1−E精度 = 1 - E精度=1−E

2.查准率、查全率与F1

2.1 查准率、查全率

错误率与精度虽然很常用，但是并不能满足所有任务需求。比如如果我们关心的是被预测为正样本中有多少比例是真的正样本，或者所有的正样本中有多少比例被预测为正样本，这个时候错误率就不够用了，还需要使用其他的性能度量。查准率(precision，准确率)与查全率(recall，召回率)就是更适用于此类需求的性能度量。

对于二分类问题，可以将样例根据其真实类别与分类器预测类别的组合划分为以下四种情形：

• 真正例(true positive)：预测为正，真实也为正
• 假正例(false positive)：预测为正，但真实为反
• 真反例(true negative)：预测为反，真实也为反
• 假反例(true negative)：预测为反，但真实为正

我们令TP、FP、TN、FN分别表示其对应的样例数，分类结果的 “混淆矩阵”(confusion matrix)如下所示：



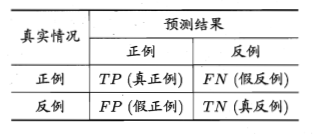
以上这四种情形理解起来都不难，但是记忆起来却总是感觉很容易混淆，可能这也是称为混淆矩阵的原因吧(手动狗头)。

下面以我个人对这四种情形记忆的一个小技巧：从预测结果入手。其实也就是我前面介绍这四个概念的时候文字解释的部分，正/反例其实是根据预测结果来的，然后结合真实情况，看看是真的正/反例还是假的正/反例。举个例子：假反例，也就是说预测为反例，但是真实情况为正例，所以叫做假 反例。

很显然，TP+FP+TN+FN = 样例总数。

从而查准率P、查全率R分别定义为：

• P=TPTP+FPP = \frac{TP}{TP+FP}P=TP+FPTP​，也就是：所有预测为正的样例中，真的正例所占比例
• R=TPTP+FNR = \frac{TP}{TP+FN}R=TP+FNTP​，也就是：所有真实为正的样例中，真的正例所占比例

查准率与查全率是一对矛盾的度量。一般来说，查准率高时，查全率往往偏低；查全率高时，查准率往往偏低。通常只有在一些简单任务中，才能使查准率和查全率都很高。

2.2 P-R曲线(P、R到F1的思维过渡)

在很多情形下，学习器的预测结果是一个实值或概率预测，因此我们可以根据此预测结果对样例进行排序，排在前面的是学习器认为“最可能”是正例的样本，排在最后的则是学习器认为“最不可能”是正例的样本。

按照上面的顺序逐个把样本作为正例进行预测，则每次可以计算出当前的查准率、查全率。以查准率为纵轴、查全率为横轴作图，就得到了查准率-查全率曲线，简称“P-R曲线”，显示该曲线的 图称为“P-R图”。如下图所示：



“平衡点”(Break-Even Point，BEP)：在P-R曲线中“查准率=查全率”时的取值。

P-R图直观地显示出学习器在样本总体上的查准率、查全率。在进行比较时：

• 若一个学习器的P-R曲线被另一个学习器的曲线完全“包住”，则可以断言后者的性能优于前者。例如上图中，学习器A的性能优于学习器C。
• 若两个学习器的P-R曲线有交叉，就难以一般性地断言两者哪个更优。一个比较合理的判据是比较P-R曲线下面积的大小，但是这个值不容易估算。于是就设计了平衡点(BEP)，通过比较平衡点的值判断学习器的性能，平衡点值较大的学习器性能较优。例如上图中，学习器B的BEP是0.74，学习器A的BEP是0.8，则可认为学习器A的性能优于学习器B。
• 但是BEP还是过于简化了些，更常用的是F1度量。

2.3 F1度量

F1是基于查准率与查全率的调和平均(harmonic mean)定义的：

1F1=12∗(1P+1R)\frac{1}{F1}=\frac{1}{2}*(\frac{1}{P}+\frac{1}{R})F11​=21​∗(P1​+R1​)

注：调和平均数又称倒数平均数，是总体各统计变量倒数的算术平均数的倒数。

于是有F1的计算公式：

F1=2∗P∗RP+R=2∗TP样例总数+TP−TNF1 = \frac{2*P*R}{P+R}=\frac{2*TP}{样例总数+TP-TN}F1=P+R2∗P∗R​=样例总数+TP−TN2∗TP​

在一些应用中，对查准率和查全率的重视程度有所不同。例如，在商品推荐系统中，为了尽可能少打扰用户，更希望推荐内容确实是用户感兴趣的，此时查准率更重要；在逃犯信息检索系统中，更希望尽可能少漏掉逃犯，此时查全率更重要。

F1度量的一般形式-FβF_βFβ​，能让我们表达出对查准率/查全率的不同偏好。FβF_βFβ​则是加权调和平均：

1Fβ=11+β2∗(1P+β2R)\frac{1}{F_β}=\frac{1}{1+β^2}*(\frac{1}{P}+\frac{β^2}{R})Fβ​1​=1+β21​∗(P1​+Rβ2​)

注：与算术平均(P+R2\frac{P+R}{2}2P+R​)和几何平均(P∗R\sqrt{P*R}P∗R​)相比，调和平均更重视较小值。

于是有FβF_βFβ​的计算公式：

Fβ=(1+β2)∗P∗R(β2∗P)+RF_β = \frac{(1+β^2)*P*R}{(β^2*P)+R}Fβ​=(β2∗P)+R(1+β2)∗P∗R​，其中β>0度量了查全率对查准率的相对重要性。

• β = 1，退化为标准的F1
• β > 1，查全率有更大影响
• β < 1，查准率有更大影响

2.4 扩展

很多时候我们有多个二分类混淆矩阵，例如进行多次训练/测试，每次得到一个混淆矩阵；或是在多个数据集上进行训练/测试，希望估计算法的“全局”性能；或是执行多分类任务，每两两类别的组合都对应一个混淆矩阵；…总之，我们希望在n个二分类混淆矩阵上综合考察查准率和查全率。

• 一种直接的做法：先在各混淆矩阵上分别计算出查准率、查全率，记为(P1,R1),(P2,R2),...,(Pn,Rn)(P_1,R_1),(P_2,R_2),...,(P_n,R_n)(P1​,R1​),(P2​,R2​),...,(Pn​,Rn​) ，再计算平均值，这样就得到了“宏查准率”(macro-P)、“宏查全率”(macro-R)、“宏F1”(macro-F1)。
  
  macroP=1n∑i=1nPimacroR=1n∑i=1nRimacroF1=2∗macroP∗macroRmacroP+macroRmacroP = \frac{1}{n}\sum_{i=1}^{n}P_i \\
  macroR = \frac{1}{n}\sum_{i=1}^{n}R_i \\
  macroF1 = \frac{2*macroP*macroR}{macroP+macroR}
  macroP=n1​i=1∑n​Pi​macroR=n1​i=1∑n​Ri​macroF1=macroP+macroR2∗macroP∗macroR​
• 还可先将各混淆矩阵的对应元素进行平均，得到TP、FP、TN、FN的平均值，分别记为TP‾、FP‾、TN‾、FN‾\overline{TP}、\overline{FP}、\overline{TN}、\overline{FN}TP、FP、TN、FN，再基于这些平均值计算出“微查准率”(micro-P)、“微查全率”(micro-R)、“微F1”(micro-F1)。
  
  microP=TP‾TP‾+FP‾microR=TP‾TP‾+FN‾macroF1=2∗microP∗microRmicroP+microRmicroP = \frac{\overline{TP}}{\overline{TP}+\overline{FP}} \\
  microR = \frac{\overline{TP}}{\overline{TP}+\overline{FN}} \\
  macroF1 = \frac{2*microP*microR}{microP+microR}
  microP=TP+FPTP​microR=TP+FNTP​macroF1=microP+microR2∗microP∗microR​

参考：

《机器学习》2.3，周志华。