某科学的PID算法学习笔记

　　最近，在某社团的要求下，自学了PID算法。学完后，深切地感受到PID算法之强大。PID算法应用广泛，比如加热器、平衡车、无人机等等，是自动控制理论中比较容易理解但十分重要的算法。

　　下面是博主学习过程中所做的笔记，笔记后面提供了4种编程语言的仿真代码（C, C++, Python, Matlab)，使实现方式更加灵活，同时增强对PID的理解。(文章较长，可点击右侧目录选择性阅读）

---

PID算法学习笔记

参考：PID基础入门教程

一、位式控制算法

　　1.1 位式控制算法原理

　　位式控制算法，通过比较SV(设定值)和PV(当前值)，输出高低电平给执行部件，执行部件（如开关）通过执行/停止来控制目标（如加热器），控制对象通过传感器将当前值反馈给控制算法，如图1。

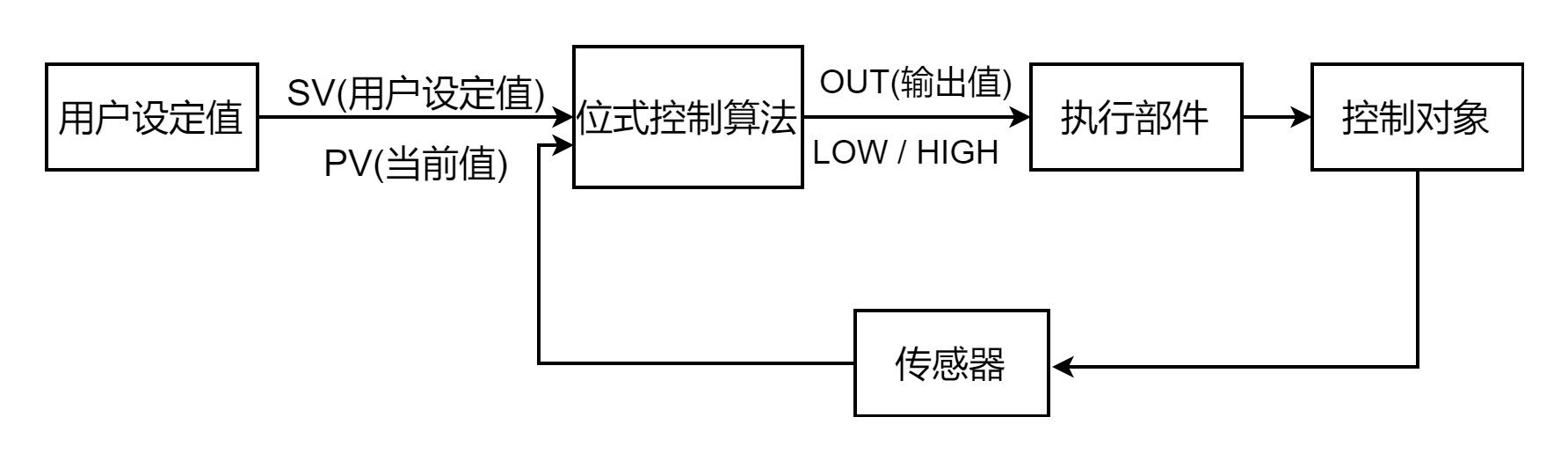
图1 位式控制算法简单应用

　　1.2 位式控制算法特点

　　位式控制算法具有如下特点：

　　　　（1）输出信号一般只有两种状态(LOW / HIGH)。

　　　　（2）通过比较SV和PV的值来产生OUT值，比如PV < SV输出高电平，PV > SV输出低电平。

　　　　（3）只比较控制对当前的状态值。

　　1.3 位式控制算法缺陷

　　位式控制算法的缺陷：

　　　　（1）输出信号单一，缺乏包容性。

　　　　（2）仅仅活在当下，没有回顾历史和展望未来。

二、PID控制算法

　　2.1 PID算法原理

　　PID控制算法，通过分析PV与SV的偏差值（包括当前偏差、历史偏差、最近偏差），输出值（PWM）经过执行器转换后应用于控制对象，控制对象通过传感器将PV反馈给PID，通过硬件寄存器等记录偏差值，以便PID随时调用，如图2。

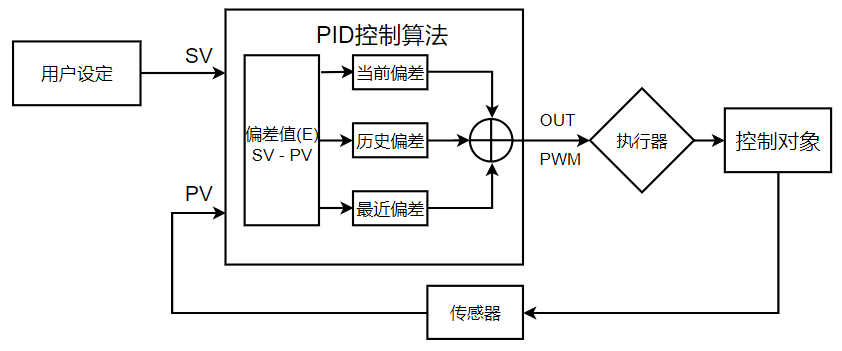
图2 PID控制算法简单应用

　　假设从“0”时刻到 k 时刻，传感器获取的状态值分别为

${X_{0}, X_{1}, X_{2}, ..., X_{k-1}, X_{k}}$

　　

　　2.2 PID比例控制

　　在2.1的条件下，设偏差值 E_k 为设定值与当前值之差，即

${E_{k}=SV-X_{k}}$

　　实际应用中的偏差值存在如下3种情况

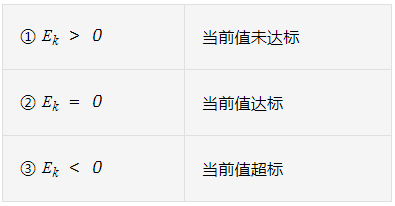
　　分析以上三种情况，不同情况下算法将输出不同值。比如算法在E_k > 0时输出较高的值，以促进当前值接近设定值。而实际应用中，控制对象的状态偏差值一般不能直接作为PWM输出值，需要进行一定比例的放大或缩小，以提高控制灵敏度。因此输出值满足关系式

${P_{out}=K_{p}\cdot E_{k}+OUT_{0}}$　　①

　　其中，P_OUT为输出值，一般与PWM有关。K_p 为比例系数，对偏差值E_k 进行一定比例的放大或缩小。OUT₀ 是当偏差值为 0 时，算法的输出值，防止负载失控。分析公式可知，偏差值E_k 越大，输出值越大，当前值接近设定值的速度越快，当前值超过设定值时，E_k < 0, 算法输出负值，当前值减小。往复循环，直到当前值稳定在设定值的误差允许范围内。

　　2.3 PID积分控制

　　在2.2的条件下，将历史偏差相加，其和为

${S_{k}=E_{0}+E{1}+E_{2}+...+E_{k-1}+E_{k}}$

　　实际应用中的历史偏差值之和存在如下3种情况

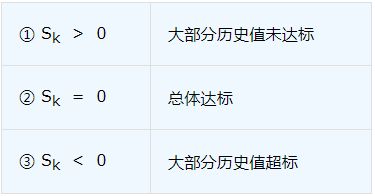
　　不同情况下输出值应不同，分析以上情况，可以令输出值满足关系式

${I_{out}=K_{p}\cdot S_{k}+OUT_{0}}$　　②

　　其中I_out为输出值，K_p为比例系数，S_k为历史偏差和，OUT₀为初始值。通过上述算法，可以对控制对象的历史状态值进行评估，根据历史状态判断输出值的大小。这种方法比较局限，因为当历史值较多时，当前值的变化将很难引起输出值改变，因此积分控制一般不会从0开始启动，当当前值接近设定值时才开启积分控制，以减少参考的历史值。

　　2.4 PID微分控制

　　在2.2的条件下，将最近两次偏差值相减，其差为

_{${D_{k}=E_{k}-E_{k-1}}$}

　　实际应用中的最近偏差值之差存在如下3种情况

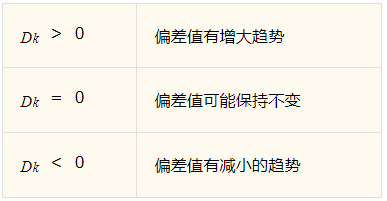
　　不同情况下输出值应不同，分析以上情况，可以令输出值满足关系式

${D_{out}=K_{p}\cdot D_{k}+OUT_{0}}$　　③

　　其中D_out为输出值，K_p为比例系数，S_k为历史偏差和，OUT₀为初始值。通过最近偏差值之差，判断偏差值的变化趋势，预测未来的偏差值大小，从而输出对应的PWM。

　　2.5 PID算法模型

　　根据以上分析，每种控制算法均有较大局限。因此综合①②③算法，令输出值为

${PID_{out_{k}}=P_{out}+I_{out}+D_{out}}$

　　代入①②③关系式，并进行简单归并，得到关系式

${PID_{out_{k}}=K_{p}\cdot \left ( E_{k}+S_{k}+D_{k}\right )+OUT_{0}}$　　④

　　分析上式中 S_k , D_k 的值，假设T为计算周期，即每次运行算法的时间间隔，T_i为积分时间常数，用于控制积分算法对输出值的影响因数，T_d为微分时间常数，用于控制微分算法对输出值的影响。

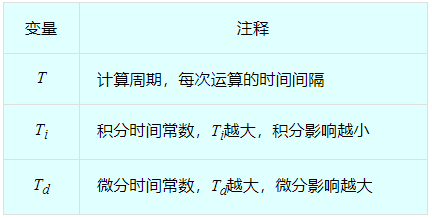
　　综上，积分控制S_k满足关系式

${S_{k}=\frac{1}{T_{i}}\cdot\sum_{k=0}^{k}E_{k} \cdot T}$   ⑤

　　微分控制D_k满足关系式

${D_{k}=T_{d}\cdot\frac{\left ( E_{k}-E_{k-1}\right )}{T}}$   ⑥

　　综合④⑤⑥，并进行简单的归并处理后，得到PID的输出关系式

${PID_{out_{k}}=P\left (K_{p}\cdot E_{k} \right )+I\left (K_{p}\cdot \frac{T}{T_{i}}\cdot \sum_{k=0}^{k}\cdot E_{k} \right )+D\left [K_{p}\cdot \frac{T_{d}}{T}\cdot\left(E_{k}-E_{k-1}\right) \right ]}$   ⑦

　　其中P，I，D分别表示比例，积分，微分控制。通过调整 K_p ，T_i ，T_d 的值来调整P， I，D对输出值的影响权重，从而使当前值更快接近并稳定在设定值误差允许范围内。

　　上述算法有一个明显的特点，即计算结果输出为PWM值，直接控制负载。因此又被称为“位置式PID算法“

　　

　　2.6 增量式PID算法

　　实际应用中，大部分控制系统具有记忆功能，可以记录每个时刻状态值，因此为了减小累加产生的运算负担，可以采用计算“增量”的方式来输出控制信号。

　　增量式PID算法的特点是只计算增加（减小）值，历史值加上增加值即为输出值，满足关系式

${\Delta PID_{out}=PID_{out_{k}}-PID_{out_{k-1}}}$   ⑧

　　代入④关系式，

${\Delta PID_{out}=P\left [K_{p}\cdot \left ( E_{k}-E_{k-1}\right ) \right ]+I\left (K_{p}\cdot \frac{T}{T_{i}}\cdot E_{k} \right )+D\left [K_{p}\cdot \frac{T_{d}}{T}\cdot \left ( E_{k}-2E_{k-1}-E_{k-2}\right ) \right ]}$  ⑨

　　对比⑧式和⑦式，⑧式运算量更小。因此对于有记忆功能的硬件系统，可以使用增量式PID算法，以减少运算，提升性能。

---

PID仿真实验

一、问题

　　既然是仿真实验，那就应该以模拟解决生活中的问题为主，为了进行比较具体，但不复杂的仿真实验，博主绞尽脑汁，终于构造了下面这个题目。

　　在《机甲大师》动漫中，主角“单单”拥有一架语音遥控的双旋翼无人机，名叫“KAKA"。如图1，动漫第一集5:35左右，KAKA在追踪飞盘时，突然受海风影响，飞行姿态偏离水平位置。性能超高的KAKA通过内部传感器测得偏角后，迅速调整姿态，恢复水平。请对这一情形进行建模分析。

图1 被海风影响的KAKA

二、解答

　　分析题目，需要对KAKA“恢复姿态”这一现象进行分析。围绕这个问题，下面以“建立物理模型→建立数学模型→算法仿真”进行逐步分析。

　　2.1 建立物理模型

　　首先简化问题，将KAKA看作刚性直杆。如图2.1，一质量为2m，长度为2r的刚性直杆，两端垂直固定一个不计质量的直流电机。直杆可以绕中心自由旋转，初始位置相对水平线偏离θ角。

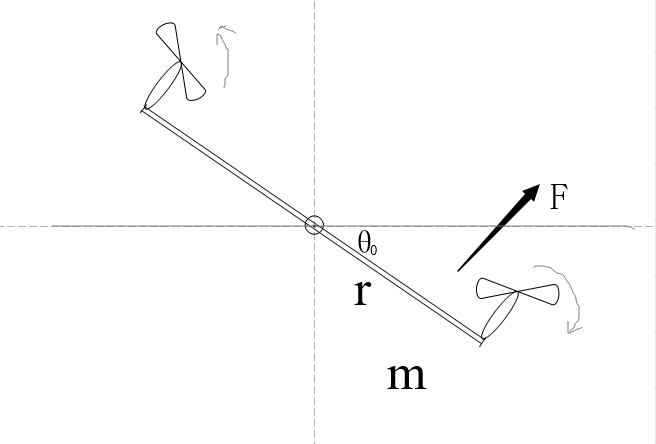
　　为了使直杆恢复水平位置，改变右端电机转速，产生“额外”升力F。

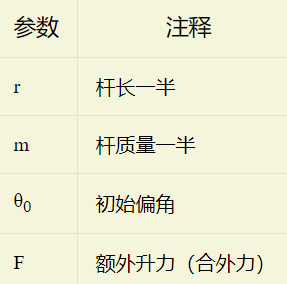
　　根据以上参数，在理想情况下，可以得到直杆的合外力矩M满足

${M = F\cdot r}$ ①

　　转动惯量J满足

${J=\frac{2}{3}mr^{2}}$ ②

　　由刚体轴转动定理

${M=J\cdot \alpha}$ ③

　　其中α为角加速度，满足关系式

${\alpha =\frac{\mathrm{d^2}\theta }{\mathrm{d} t^2}}$ ④

　　其中t为时间，联立①②③④，求解微分方程可得到关系式

${\theta _{t}=\frac{3\cdot F}{4\cdot m\cdot r}\cdot t^2}$ ⑤

　　其中θ为直杆在力合外力F的作用下，经过时间t后转动的角度。

　　2.2 建立数学模型

　　设${T}$为计算周期，在⑤式的条件下，令${t=T}$，在${T}$时间内直杆转动角度满足关系式

${\theta _{T} =\frac{3\cdot F}{4\cdot m\cdot r}\cdot T^2}$ ⑥

　　假设${F}$随时间的变化周期为${T}$，那么经过${t}$时间后，${F}$变化${n}$次，直杆转动角度满足

${\theta  =\frac{3\cdot T^2}{4\cdot m\cdot r}\cdot\sum_{n=0}^{n} F_{n}}$ ⑦

　　直杆与水平线的当前偏差角${E_{k}}$满足

${E_{k}=\theta_{0}-\frac{3\cdot T^2}{4\cdot m\cdot r}\cdot\sum_{n=0}^{k} F_{n}}$ ⑧

　　上式即为直杆在恢复水平位置过程中，在合外力F作用下，当前偏角对于时间的函数。

　　参考实际情况，由于合外力以T为周期发生变化，该偏角函数曲线应如满足图2.2

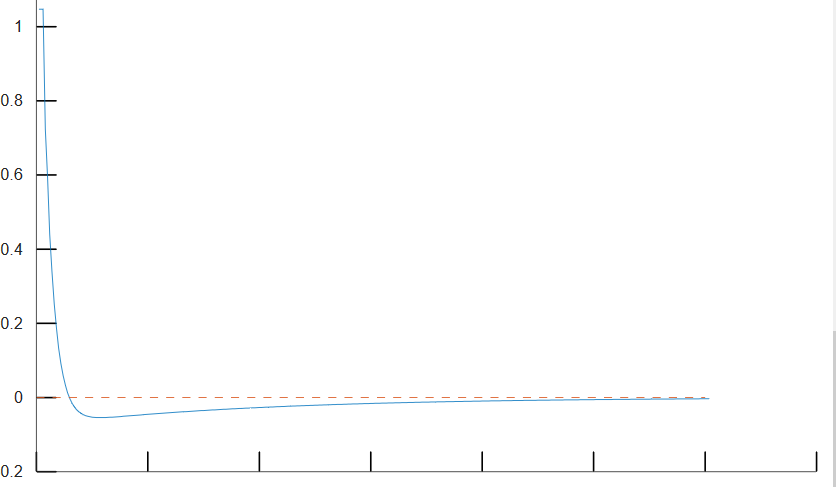
图2.2 （预测）直杆偏角对于时间的变化曲线

　　分析上图曲线，发现其变化趋势可以用PID算法进行拟合。

　　2.3 PID算法仿真

　　分析关系式⑧，其中${T}$可以看作采样周期，${F}$为算法输出值，${E_{k}}$为当前偏差角。应用位置式${PID}$算法，设比例系数为${K_{p}}$，积分时间常数为${T_{i}}$，微分时间常数为${T_{d}}$，输出值满足PID算法关系式

${F_{out_{k}}=K_{p}\cdot E_{k} +K_{p}\cdot \frac{T}{T_{i}}\cdot \sum_{k=0}^{k}\cdot E_{k} + K_{p}\cdot \frac{T_{d}}{T}\cdot E_{k}-E_{k-1}}$ ⑨

　　分析⑧式，为了简化计算，不妨令

${m = 0.3}$,  ${r=0.1}$,  ${\theta _{0}=\frac{\pi}{3}}$ （${SI}$）

　　则当前偏差角满足

${E_{k}=\frac{\pi}{3}-25\cdot T^2\cdot\sum_{n=0}^{k} F_{out_{n}}}$ ⑩

　　综上，可以假设如表2.3中的参数

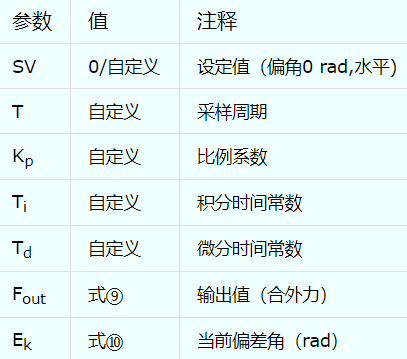
表2.3 PID参数

　　下面，在上述模型条件下，用5种编程语言(Matlab, C, C++, Python)进行算法仿真。

---

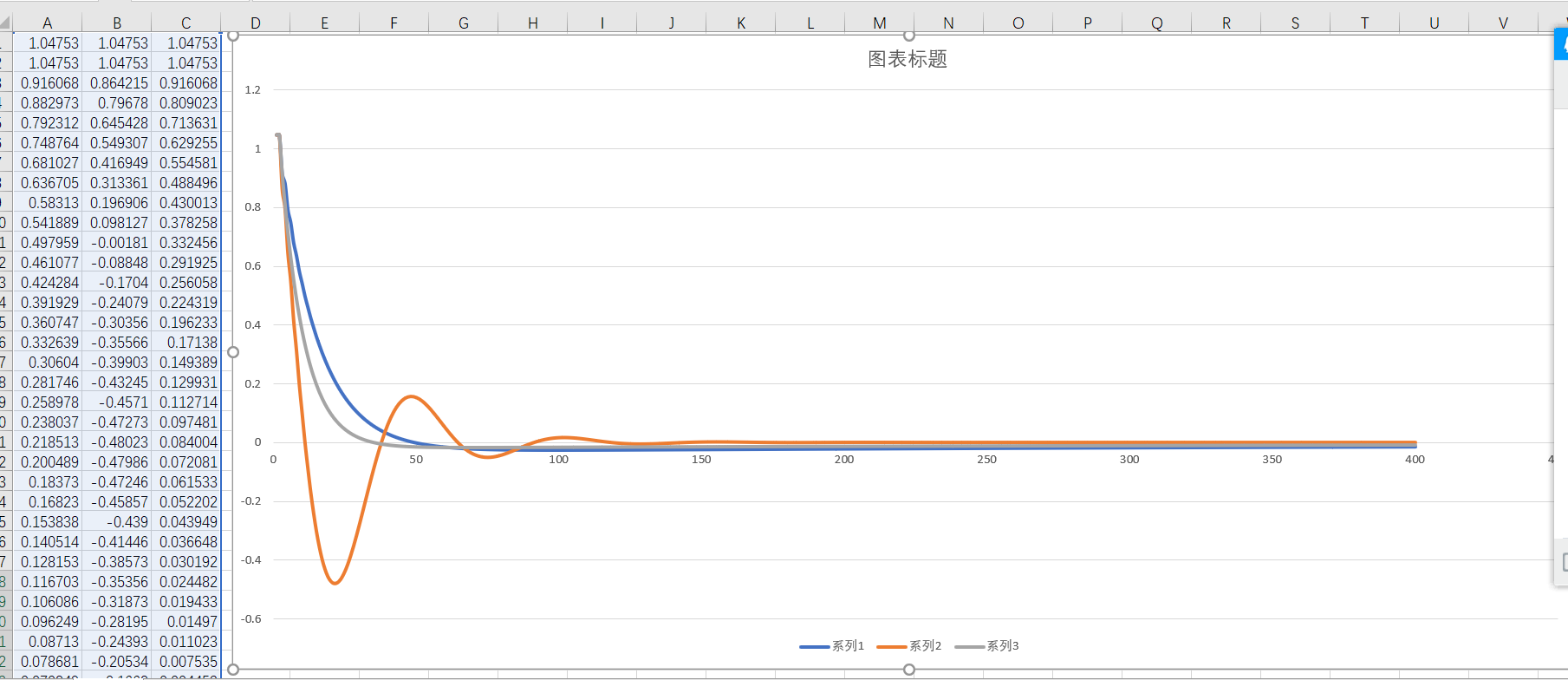
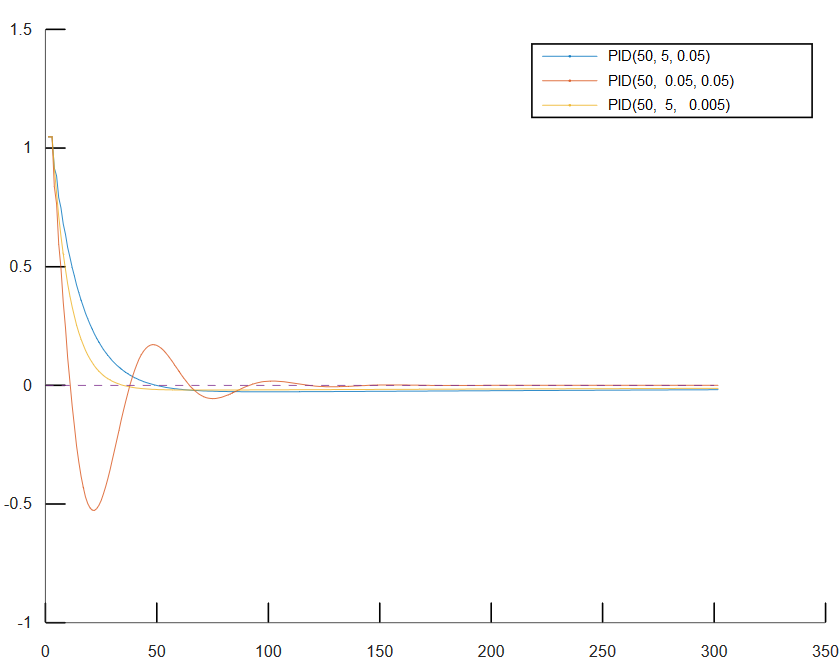
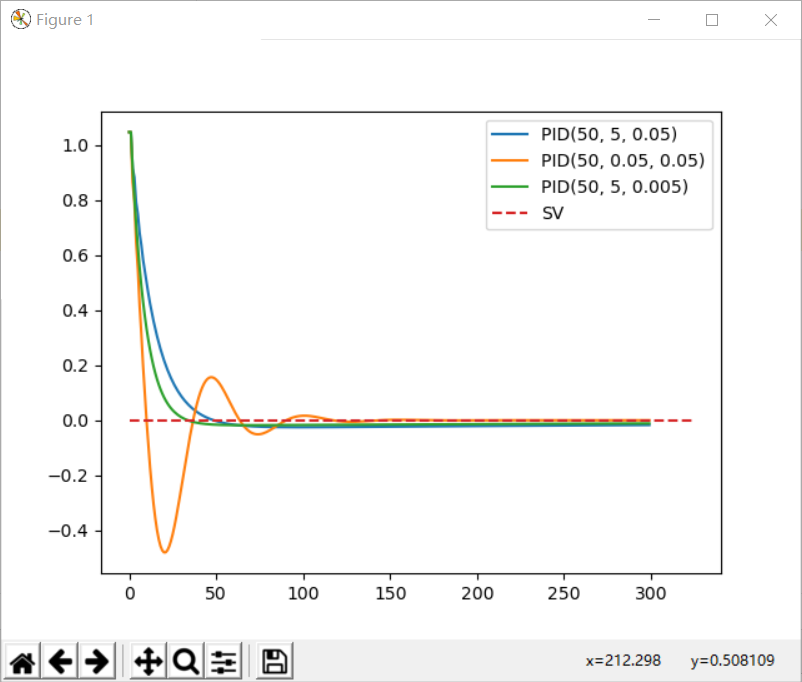
1) Matlab

比较方便，可以先通过Matlb仿真确定PID系数

　　源码：

clear,clc,close all % 清屏
 
syms x
SV = 0; % 设定值，角（弧）度 0 (rad)
T = 0.01; % 计算周期/采样周期
Kp = 50; % 比例系数
Ti = 5;  % 积分时间常数
Td = 0.05; % 微分时间常数
 
E = []; % 历史偏差
Fout = []; % 输出值，升力
E(1) = pi ./3; % 初始角度 π/3 (rad)
 
for i = 1:1:3 % 绘制3种比较曲线
    if i == 2;
        Kp = 50;  % 比例系数
        Ti = 0.05;   % 积分时间常数
        Td = 0.05; % 微分时间常数
        E = []; % 历史偏差
        Fout = []; % 输出值，升力
        E(1) = pi ./3; % 初始角度 π/3 (rad)
    end % if i ==2
 
    if i ==3;
        Kp = 50;  % 比例系数
        Ti = 5;   % 积分时间常数
        Td = 0.005; % 微分时间常数
        E = []; % 历史偏差
        Fout = []; % 输出值，升力
        E(1) = pi ./3; % 初始角度 π/3 (rad)
    end % if i ==3
 
    for t = 0:0.01:3; % 计算300次
        k = round(t*100 + 2); % 当前指数
 
        E(k) = E(1) - 25*(T^2)*sum(Fout); % 获取当前值
 
        %#### 核心，PID计算输出值 ####%
        if k>2;
            if E(k) != 0;
                Fout(k) = Kp*(E(k) + (T./Ti)*sum(E) + (Td./T)*(E(k)-E(k-1)));
            end % end if E(k) !=0
        end % end if k>2
        %#############################%
 
        k++; % 当前指数+1
 
    end % end for 计算400次
 
    hold on
    plot(E) % 显示数据图
end # for 绘制3种比较曲线
 
legend('PID(50, 5, 0.05)','PID(50,  0.05, 0.05)','PID(20,  5,   0.005)')
 
hold on
plot([0,300],[0,0],'--'); % 显示参考线，斜率0，截距0

　　运行结果

---

2) C语言

 /**@file     main.c
 * @brief     位置式PID  C语言算法仿真
 * @author    BROSY
 * @copyright CSU | BROSY
 ********************************************************************************/
 
 /*************************************************************************************
 注：以便查阅，我将所有函数和声明都放在main.c中，进行项目实践时，再设计文件架构
 *************************************************************************************/
 
 #include<stdio.h>
 #define PI (3.1416)
 
 typedef struct {
     const int SV = ; // 设定值（弧度rad)
 
     double InitVal;        //初始偏差值
     double T;            // 采样周期
     double Kp;        // 比例系数
     double Ti;        // 积分时间常数
     double Td;        // 微分时间常数
     double Ek;        //当前偏差
     double SumEk;    //历史偏差之和
     double Ek_1;        //上次偏差
     double SumFout;    // 输出值之和
 }PID_Structure;
 
 /**
 @brief    位置式PID输出函数
 @param    [in] PID结构体
 @return    算法输出值（额外升力）
 */
 double PID_OUT(PID_Structure* PID)
 {
     double Fout;
     Fout = PID->Kp * (PID->Ek
         + (PID->T / PID->Ti) * PID->SumEk
         + (PID->Td / PID->T) * (PID->Ek - PID->Ek_1));
 
     return Fout;  // 输出值（额外升力）
 }
 
 /**
 @brief    获取当前偏差值
 @param    [in] PID结构体, 历史输出值（数组）
 @return    kaka当前状态偏差值
 */
 double GetCurrE(PID_Structure PID)
 {
     double Ek;
     Ek = PID.InitVal -  * (PID.T * PID.T) * PID.SumFout;
     return Ek;
 }
 
 int main()
 {
     PID_Structure PID; // 创建PID
 
     PID.InitVal = PI / ;
     PID.T = 0.01;
     PID.Kp = ;
     PID.Ti = ;
     PID.Td = 0.005;
     PID.Ek = ;
     PID.Ek_1 = ;
     PID.SumFout = ;
     PID.SumEk = ;
 
     // 计算400次
     for (int i = ; i < ; i++)
     {
         if (i > )
         {
             PID.Ek_1 = PID.Ek; // 获取k-1的偏差值
         }
         PID.Ek = GetCurrE(PID); // 获取当前偏差值
         PID.SumEk += PID.Ek; // 历史偏差之和
 
         printf("%f\n", PID.Ek);
         if (PID.Ek !=  && i > ) // 误差
         {
             PID.SumFout += PID_OUT(&PID); // 获取输出值之和
 
         }
         else
         {
             PID.SumFout += ; // 储存输出值
         }
     }
 
 }

//C show all

将输出结果导入到excel中并绘制曲线：

---

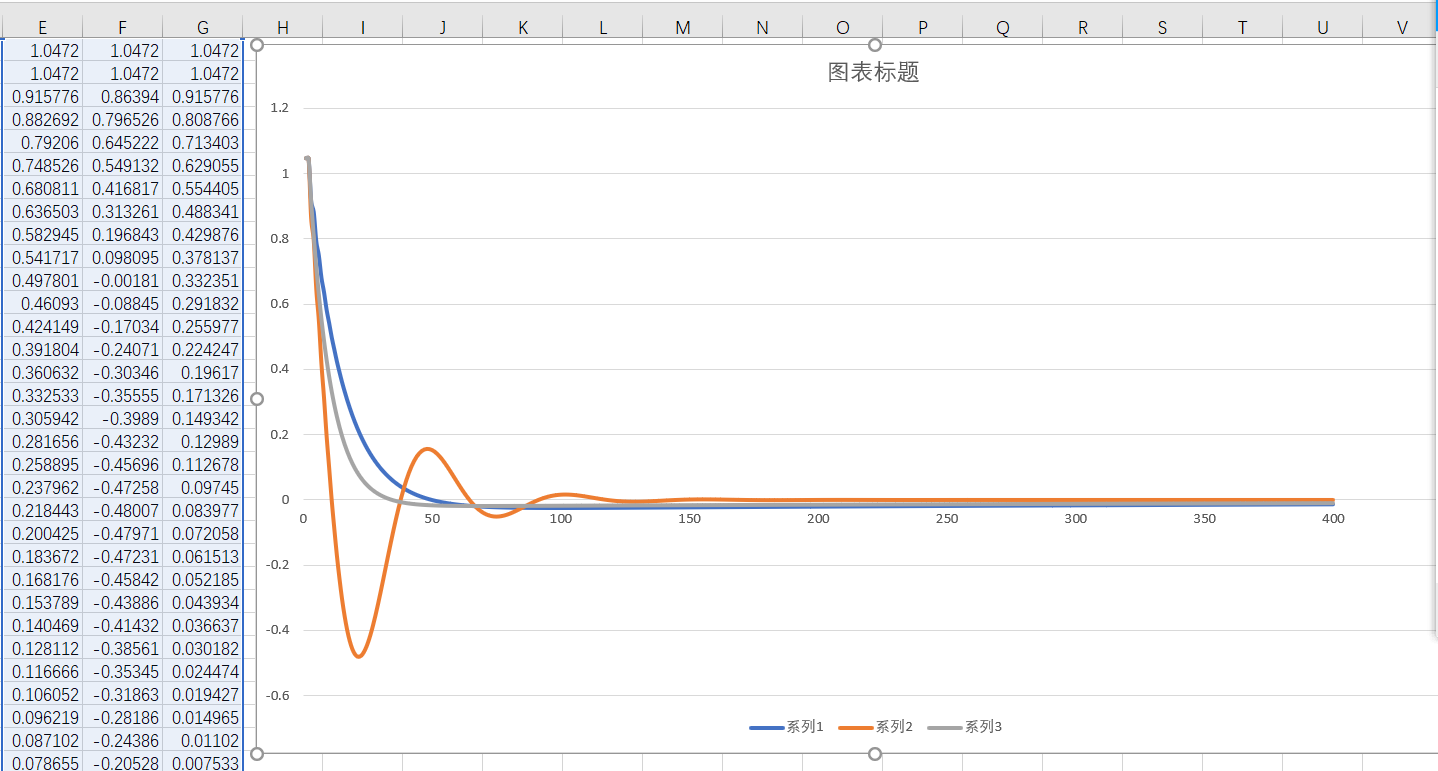
3) C++

 /**@file     main.cpp
 * @brief     位置式PID  C语言算法仿真
 * @author    BROSY
 * @copyright CSU | BROSY
 ********************************************************************************/
 
 #include "PID.h"
 
 int main()
 {
     PID* pid[]; // 创建PID
 
     pid[] = new PID(, , 0.05); // 初始化PID1
     pid[] = new PID(, 0.05, 0.05); // 初始化PID2
     pid[] = new PID(, , 0.005); // 初始化PID3
 
     for (int i = ; i < ; i++)
     {
         pid[i]->Loop();// 计算400次
         delete pid[i]; // 释放内存
     }
 }

//main.cpp 展开全部

 #include "PID.h"
 #include <iostream>
 /**
 @brief    初始化PID参数
 @param    [in] P I D系数
 只设置P I D的系数，其余默认
 */
 PID::PID(double P, double I, double D)
 {
     Kp = P;
     Ti = I;
     Td = D;
 
     InitVal = (3.1426)/; // 初始偏差值π/3
     T  = 0.01;            // 采样周期
     Ek = ;            //当前偏差
     SumEk = ;        //历史偏差之和
     Ek_1 = ;            //上次偏差
     SumFout = ;        // 输出值之和
 }
 
 /**
 @brief    位置式PID输出函数
 @return    算法输出值（额外升力）
 */
 double PID::PID_OUT()
 {
     double Fout;
 
     Fout = Kp * (Ek
         + (T / Ti) * SumEk
         + (Td / T) * (Ek - Ek_1));
 
     return Fout;  // 输出值（额外升力）
 }
 
 /**
 @brief    获取当前偏差值
 @return    kaka当前状态偏差值
 */
 double PID::GetCurrE()
 {
     double Ek;
     Ek = InitVal -  * (T * T) * SumFout;
     return Ek;
 }
 
 /**
 @brief    循环计算并输出值
 @param    [in] 计算次数
 */
 void PID::Loop(int times)
 {
     std::cout << "计算次数：" << times << std::endl;
     std::cout << "P  = " << Kp << std::endl;
     std::cout << "I  = " << Ti << std::endl;
     std::cout << "D  = " << Td << std::endl<<std::endl;
 
     for (int i = ; i < times; i++)
     {
         if (i > )
         {
             Ek_1 = Ek; // 获取k-1的偏差值
         }
         Ek = GetCurrE(); // 获取当前偏差值
         SumEk += Ek; // 历史偏差之和
 
         std::cout << Ek << std::endl;
         if (Ek !=  && i > ) // 误差
         {
             SumFout += PID_OUT(); // 获取输出值之和
 
         }
         else
         {
             SumFout += ; // 储存输出值
         }
     }
 }

//PID.cpp

#pragma once
class PID
{
private:
    const int SV = ; // 设定值（弧度rad)
 
    double InitVal;        //初始偏差值
    double T;            // 采样周期
    double Kp;        // 比例系数
    double Ti;        // 积分时间常数
    double Td;        // 微分时间常数
    double Ek;        //当前偏差
    double SumEk;    //历史偏差之和
    double Ek_1;        //上次偏差
    double SumFout;    // 输出值之和
 
public:
    PID(double P, double I, double D); // PID初始化，只输入PID系数，其余默认
 
    double PID_OUT(); // PID算法核心，计算输出值
    double GetCurrE(); // 获取当前值
 
    void Loop(int times); // 循环计算输入计算次数
};

//PID.h

将输出结果导入到excel中并绘制曲线：

---

4) Python

 import matplotlib.pyplot as plt  # 导入绘图库
 import numpy as np
 
 '''
 @brief    位置式PID输出函数
 @param    [in] PID结构体
 @return    算法输出值（额外升力）
 '''
 
 def pid_out():
     f_out = Kp * (Ek
                   + (T / Ti) * sum_Ek
                   + (Td / T) * (Ek - Ek_1))
     return f_out
 
 '''
 @brief    获取当前偏差值
 @param    [in] PID结构体, 历史输出值（数组）
 @return    kaka当前状态偏差值
 '''
 
 def get_curr_e():
     ek = init_val - 25 * (T ** 2) * sum_f_out
     return ek
 
 sv = 0.0  # 设定值
 init_val = (3.1416) / 3  # 初始值
 T = 0.01  # 采样周期
 times = 300  # 计算次数
 e = np.zeros(times)
 for t in range(3):
     Ek = 0.0  # 当前偏差
     sum_Ek = 0.0  # 历史偏差之和
     Ek_1 = 0.0  # 上一次偏差
     sum_f_out = 0.0  # 输出值之和（升力）
 
     if t == 0:
         Kp = 50  # 比例系数
         Ti = 5  # 积分时间常数
         Td = 0.05  # 微分时间常数
     if t == 1:
         Kp = 50  # 比例系数
         Ti = 0.05  # 积分时间常数
         Td = 0.05  # 微分时间常数
     if t == 2:
         Kp = 50  # 比例系数
         Ti = 5  # 积分时间常数
         Td = 0.005  # 微分时间常数
 
     '''
     @brief    循环计算并输出值
     @param    [in] 计算次数
     '''
     for i in range(times):
         if i > 0:
             Ek_1 = Ek
 
         Ek = get_curr_e()  # 获取当前值
         sum_Ek = sum_Ek + Ek  # 获取历史值之和
 
         e[i] = Ek  # 储存当前值，方便后面绘图
 
         if Ek != 0 and i > 0:
             sum_f_out = sum_f_out + pid_out()  # 获取输出值之和
 
     plt.plot(e, label='PID({0}, {1}, {2})'.format(Kp, Ti, Td))  # 画曲线图，显示PID图例
 
 plt.plot(np.zeros(times + 25), label='SV', linestyle='--')  # 设定值
 plt.legend()  # 显示图例
 
 plt.show()

#

下载源码

链接：PID仿真源码    密码：hhh