SD 胡策 Round 1 T3 彩尾巴猹的二进制数

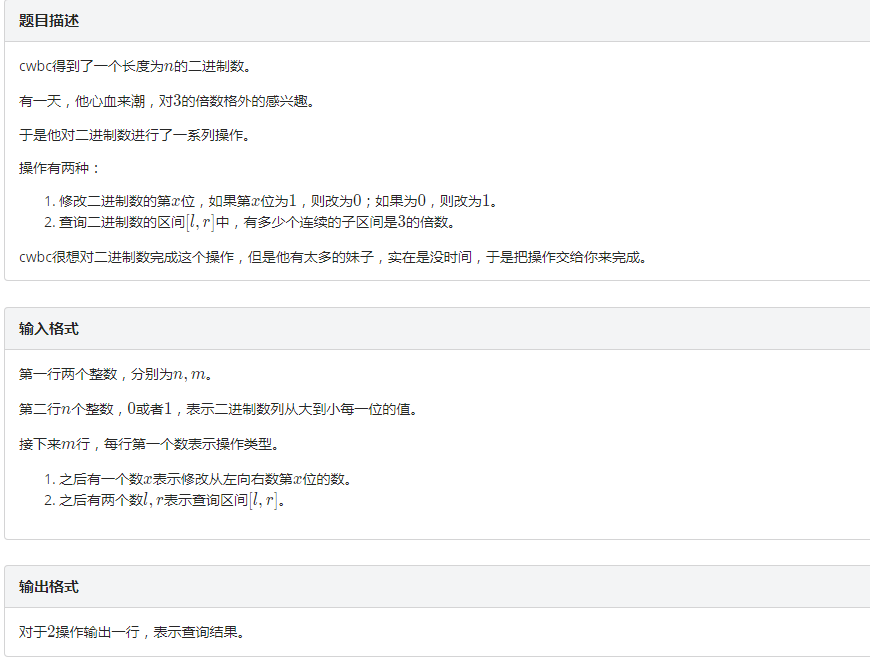
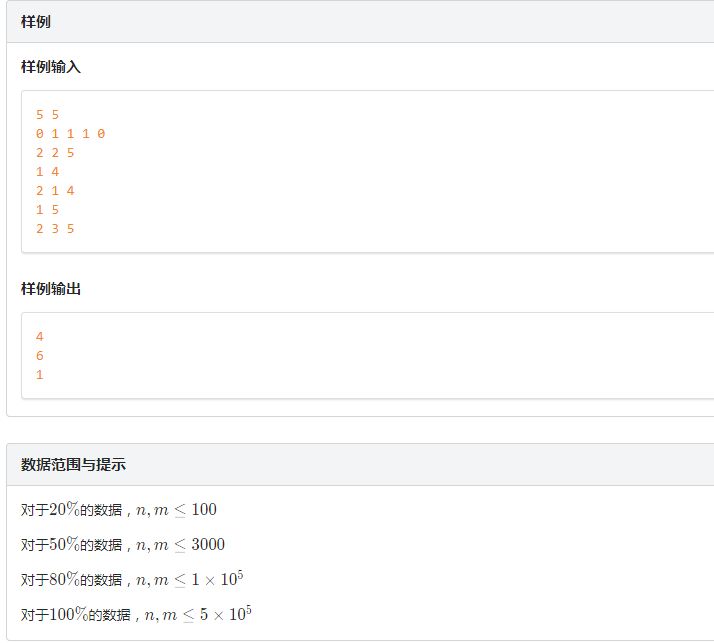
发现一个区间[L,R]代表的2进制数是3的倍数，当且仅当从L开始的后缀二进制值 - 从R+1开始的后缀二进制值 是 3 的倍数 (具体证明因为太简单而被屏蔽)。

于是我们就可以在每个点维护从它开始的后缀二进制数的值，因为在%3同余系下只有3个数，所以我们可以很容易的用线段树进行区间维护，然后答案就是 C(num[0],2) + C(num[1],2) + C(num[2],2)    [注意如果查询区间是 [l,r]的话那么 在线段树中查找的区间是 [l,r+1] ，因为区间[x,y]对应 x和y+1后缀相减]。

但是有修改咋办呢？

给每个位置设一个权值，后缀长度是奇数的权值是1，反之则是2。

然后稍微动脑子想一下，如果  一个位置修改前是 1  和  这个位置权值是 1  这两个条件只满足其中一个，那么就是对前缀区间 +1；否则就是对前缀区间+2。

所以随便写个线段树打打标记就好啦。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
const int maxn=500005;
int a[maxn],val[maxn],tag[maxn*4];
int n,m,sum[maxn*4][3],hz[maxn];
int le,ri,W,opt,ans[3];

inline int read(){
	int x=0; char ch=getchar();
	for(;!isdigit(ch);ch=getchar());
	for(;isdigit(ch);ch=getchar()) x=x*10+ch-'0';
	return x;
}

inline int add(int x,int y){ x+=y; return x>=3?x-3:x;}

inline void maintain(int o,int lc,int rc){
	sum[o][0]=sum[lc][0]+sum[rc][0];
	sum[o][1]=sum[lc][1]+sum[rc][1];
	sum[o][2]=sum[lc][2]+sum[rc][2];
}

inline void CG(int o,int VAL){
	int T=sum[o][0];
	tag[o]=add(tag[o],VAL);
	if(VAL==1){
		sum[o][0]=sum[o][2];
		sum[o][2]=sum[o][1];
		sum[o][1]=T;
	}
	else{
		sum[o][0]=sum[o][1];
		sum[o][1]=sum[o][2];
		sum[o][2]=T;
	}
}

inline void pushdown(int o,int lc,int rc){
	if(tag[o]){
		CG(lc,tag[o]),CG(rc,tag[o]);
		tag[o]=0;
	}
}

void build(int o,int l,int r){
	if(l==r){
		sum[o][hz[l]]++;
		return;
	}
	int mid=l+r>>1,lc=o<<1,rc=(o<<1)|1;
	build(lc,l,mid),build(rc,mid+1,r);
	maintain(o,lc,rc);
}

void update(int o,int l,int r){
	if(l>=le&&r<=ri){
		CG(o,W);
		return;
	}
	int mid=l+r>>1,lc=o<<1,rc=(o<<1)|1;
	pushdown(o,lc,rc);
	if(le<=mid) update(lc,l,mid);
	if(ri>mid) update(rc,mid+1,r);
	maintain(o,lc,rc);
}

void query(int o,int l,int r){
	if(l>=le&&r<=ri){
		ans[0]+=sum[o][0];
		ans[1]+=sum[o][1];
		ans[2]+=sum[o][2];
		return;
	}
	int mid=l+r>>1,lc=o<<1,rc=(o<<1)|1;
	pushdown(o,lc,rc);
	if(le<=mid) query(lc,l,mid);
	if(ri>mid) query(rc,mid+1,r);
}

inline ll getC(int x){ return x?x*(ll)(x-1)>>1:0;}

inline void solve(){
	while(m--){
		opt=read();
		if(opt==1){
			le=1,ri=read();
			if(a[ri]+val[ri]==2) W=2; else W=1;
			a[ri]^=1,update(1,1,n);
		}
		else{
			le=read(),ri=read(),ri++;
			ans[0]=ans[1]=ans[2]=0;
			query(1,1,n);
			printf("%lld\n",getC(ans[0])+getC(ans[1])+getC(ans[2]));
		}
	}
}

int main(){
	n=read(),m=read();
	for(int i=1;i<=n;i++) a[i]=read();
	n++,val[n]=2,hz[n]=0;
	for(int i=n-1;i;i--){
		val[i]=3-val[i+1];
		hz[i]=add(hz[i+1],val[i]*a[i]);
	}

	build(1,1,n);
	solve();

	return 0;
}