CS231n 2016 通关 第四章-反向传播与神经网络（第一部分）

在上次的分享中，介绍了模型建立与使用梯度下降法优化参数、梯度校验，以及一些超参数的经验。

本节课的主要内容：

1==链式法则

2==深度学习框架中链式法则

3==全连接神经网络

=========================================================================================

1、链式法则

　　目前我们所处的阶段：

　　学习了SVM softmax两个模型或者算法，需要优化w》》梯度下降。

　　上述公式的计算图例：

　　由上述计算图可见，模型非常简洁，可以使用计算偏导的方式来优化参数，但是当模型非常大时，比如：

　　　　　　

　　此时直接求偏导的方法不可行。

　　解决方法》》链式法则。

　　举例：

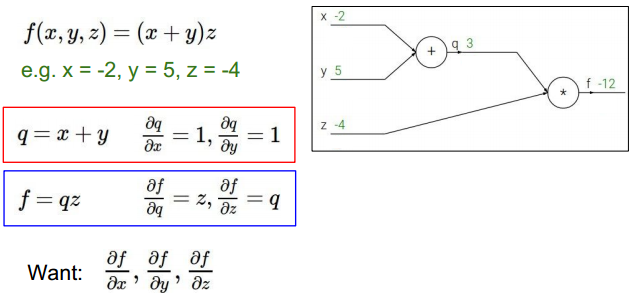
　　对具体函数用链式法则求导。首先进行前向计算。如上图。

　　求f对中间变量偏导：

　　求中间变量对初始变量的偏导，结合之前计算，得到f对初始变量的偏导》》链式法则

　　　　　　　　　　　　　　　　　　　　

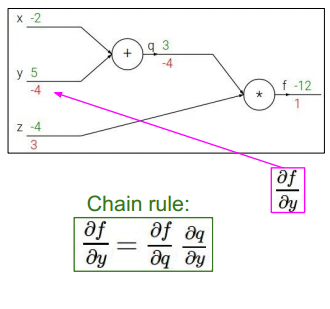
　　链式法则解释：

　　　　单一结点，输出值对输入变量的偏导：

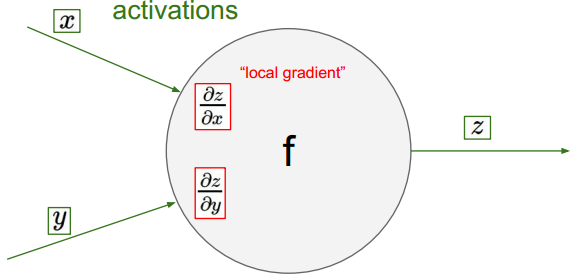
　　　　计算此结点与下一节点，联合对输入变量的偏导：

　　　　多节点：

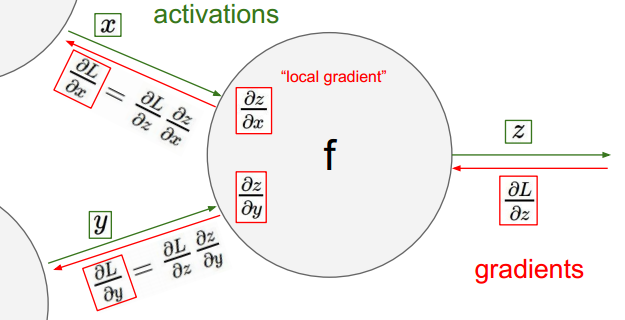
　　　　上述即为链式法则的过程。

　　实际例子：

　　　　可视化流程如上，其中已经实现了前向计算。

　　　　反向传播，首先计算最后节点：

　　　　倒数第二个节点：

　　　　按照上述方法，逐一反向计算：

　　　　　　　　

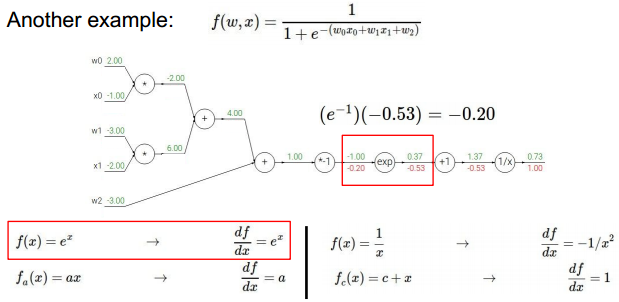
　　　　达到分支时：

　　　　　　

　　可以对某些步骤进行简化》》直接对某个表达式整体求导：

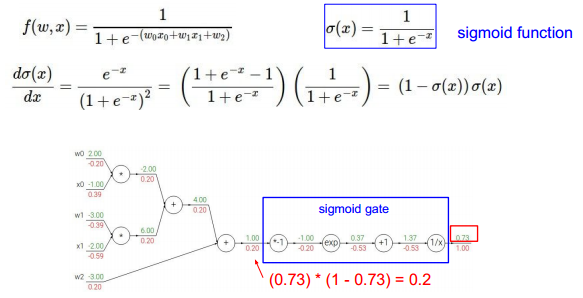
　　各种计算的链式计算以及代码结构：

　　　　加法：

　　　　　　

　　　　乘法：

　　深度学习框架实现：

　　　　　　

　　向量形式的链式法则：

　　　　Jacobian matrix：

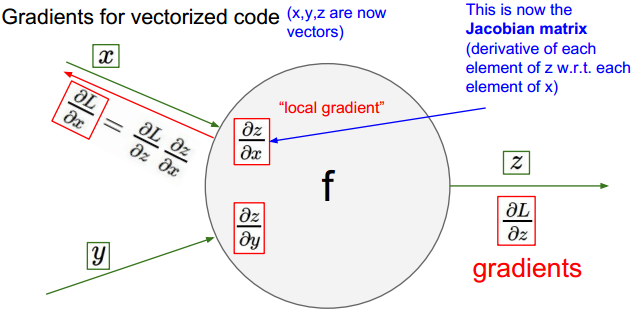
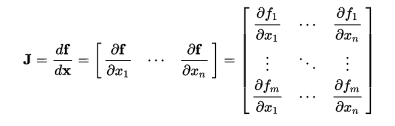
　　　　向量形式链式法则举例：

　　　　　　问题：

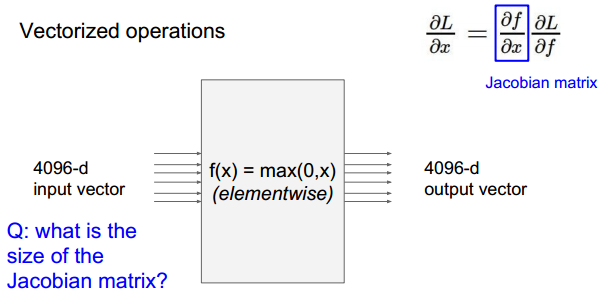
　　　　　　问题：

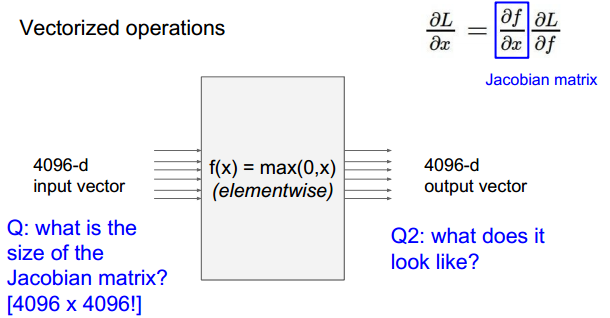
　　　　　　此时的输出如f1只与x1相关，所以对应的雅克比行列式只有在对角线上有值，为0或者1.其余元素均为0.

　　　　　　由此可见，计算雅克比矩阵的方式不是很简洁。

　　总结：

=========================================================================================

2、神经网络 Neural Network

　　两层NN与线性函数对比:

　　之前的分类器得到的可视化：

　　　　可视化的结果显示，模型将某一类的特征训练调整到单一的w（向量或矩阵），此时的w混合了很多特点，比如颜色、形状。

　　　　而NN包含了很多隐藏层，隐藏层的某个节点对应相应的某个特征，比如颜色，方向等等。将隐藏层节点得到的特征抽象到输出，可以得出结果。

　　　　两层隐藏层：

　　　　　　

　　　　代码实现：

　　　　　　其实就是层的叠加。

　　　　前向、反向传播代码结构：

　　　　具体细节在下一节课会涉及。

NN的生物学知识：

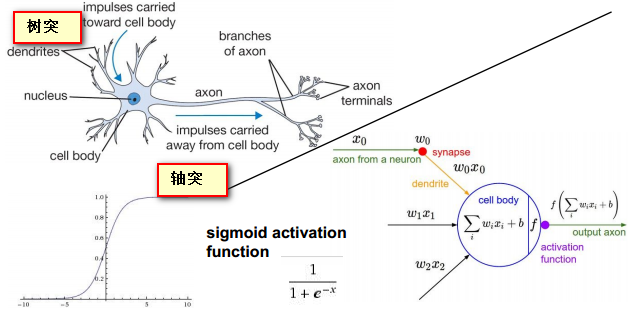
　　使用sigmoid作为激活函数。

　　神经系统中的树突如输入层到隐藏层节点的连接。轴突相当于隐藏层节点的输出与其他节点的连接。

　　代码实现（结构）：

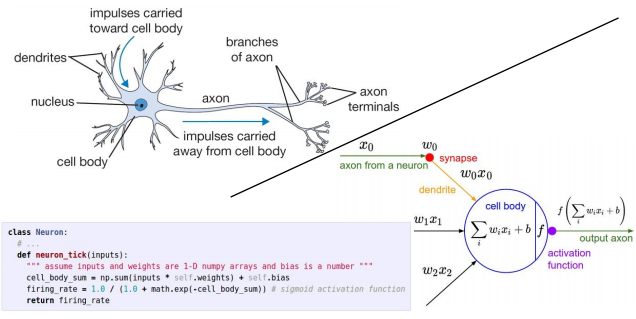
　　一些区别：

　　　　生物神经系统功能更复杂。

常用的激活函数：

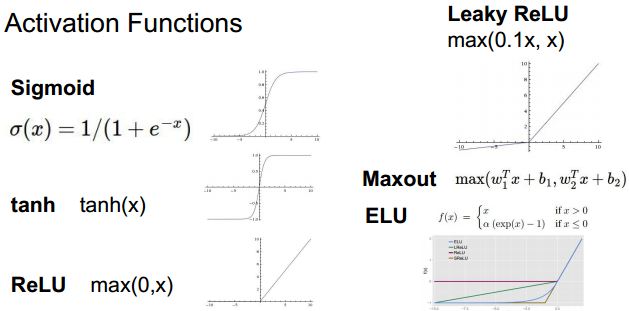
　　根据模型特点以及计算的效果，选择不同的激活函数。其中ReLU、Maxout比较常用。

　　各个激活函数的特点在课程配套的笔记中有详细说明。之后会把总结好的笔记扫描、分享出来。

NN层数：

　　下图以2 3层网络为例，层数不计输入层，注意与UFLDL进行对比，UFLDL中计入了输入层：

前向传播代码结构：

前向传播实例：

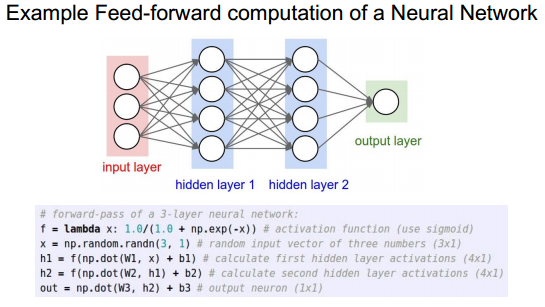
关于NN的层数：

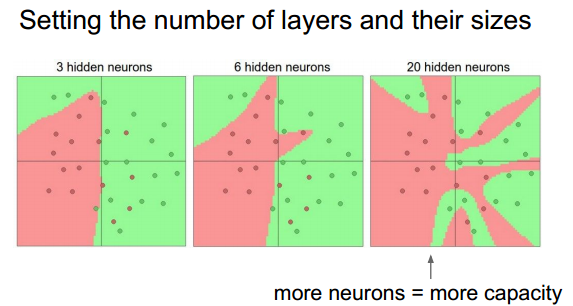
　　NN可以视为对飞线性函数的逼近》》证明可以逼近任何函数。

　　由上图可见，NN层数不同，分类的准确率也有差异，一般选取3层或以上的层数，并加入正则的方式。

　　当高于3层时，层数的增加并不能很好的改善最终的结果，甚至会产生过拟合。

　　cnn中层数较高表示抽象能力更强，希望较高的层数。

正则化强度对结果的影响：

　　可以通过选择合适的正则化强度系数控制过拟合结果。上图中看出较高的正则化强度系数使得分类界面更平滑。

=========================================================================================

总结：

下节课的内容：

附：通关CS231n企鹅群：578975100 validation：DL-CS231n