poj 3708 Recurrent Function

Recurrent Function

Time Limit: 1000MS		Memory Limit: 65536K
Total Submissions: 1233		Accepted: 336

Description

Dr. Yao is involved in a secret research on the topic of the properties of recurrent function. Some of the functions in this research are in the following pattern:

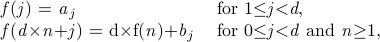
in which set {a_i} = {1, 2, …, d-1} and {b_i} = {0, 1, …, d-1}.
We denote:

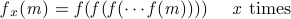
Yao's question is that, given two positive integer m and k, could you find a minimal non-negative integer x that

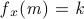
Input

There are several test cases. The first line of each test case contains an integer d (2≤d≤100). The second line contains 2d-1 integers: a₁, …, a_d-1, followed by b₀, ..., b_d-1. The third line contains integer m (0<m≤10¹⁰⁰), and the forth line contains integer k (0<k≤10¹⁰⁰). The input file ends with integer -1. 

Output

For each test case if it exists such an integer x, output the minimal one. We guarantee the answer is less than 2⁶³. Otherwise output a word "NO". 

Sample Input

2
1
1 0
4
7
2
1
0 1
100
200
-1

Sample Output

1
NO

Hint

For the first sample case, we can see that f(4)=7. And for the second one, the function is f(i)=i. 

 

题意：求解递归方程，该类方程在具体数学第一章中有明确介绍，这里只给结论，若要求解f(x)，可以先将x转化成c进制c进制一共m位,即(x_mx_m-1...x₁x₀)_{c，那么有结论：}

f((x_mx_m-1...x₁x₀)_c)=(a_xmb_xm-1b_xm-2...b_x1b_x0)c

思路：结论已介绍，可以看出将x化成c进制后每一位都在进行置换操作,c进制首位用ai来置换，后面几位都用bi来置换。那么如果将k也转化成d进制，那么如果m的d进制的每一位通过不断置换之后最终与k的每一位分别相等，置换的最小次数x就是所求。

我们设最少置换x次,m的d进制的每一位各自置换到k的每一位需要ci次,并且每一位置换足够次数会产生轮回，轮回的大小记为loop(i)

那么x满足条件：

x==c1 mod(loop(1))

x==c2 mod(loop(2))

.....

x==cn mod(loop(n))

这样就是求满足上述模方程组的最小解即可。

 

AC代码：

#define _CRT_SECURE_NO_DEPRECATE
#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<cstring>
#include<set>
#include<string>
#include<queue>
#include<cmath>
using namespace std;
#define INF 0x3f3f3f3f
const int N_MAX = +;
typedef long long ll;
// 大数类
class bign
{
#define  base  1000
#define  digit  3
private:
    int _arr[];
    int _m;
    void bign::_simplify(void)
    {
        for (int i = ; i <= _m; i++)
        {
            if (i == _m && _arr[i] >= base) _m++;
            _arr[i + ] += _arr[i] / base;
            _arr[i] %= base;
        }
    }
public:
    bign::bign(void) : _m() { memset(_arr, , sizeof(_arr)); }
    bign::bign(int init) : _m()
    {
        memset(_arr, , sizeof(_arr));
        _arr[] = init;
        _simplify();
    }
    friend istream& operator >> (istream& fin, bign& a)
    {
        char init[]; int len, b, t;
        fin >> init;
        len = strlen(init); a._m = -;
        for (int i = len - ; i >= ;)
        {
            t = , b = ;
            for (int j = ; j < digit && i >= ; j++, i--)
            {
                t += (init[i] - '') * b;
                b *= ;
            }
            a._arr[++a._m] = t;
        }
        return fin;
    }
    friend bign operator / (bign a, int b)
    {
        for (int i = a._m; i >= ; i--)
        {
            if (a._arr[i] < b && i == a._m && i != ) a._m--;
            if (i > ) a._arr[i - ] += (a._arr[i] % b) * base;
            a._arr[i] /= b;
        } return a;
    }
    friend int operator % (bign a, int b)
    {
        for (int i = a._m; i >= ; i--)
        {
            if (i == ) return a._arr[i] % b;
            else a._arr[i - ] += (a._arr[i] % b) * base;
        }
    }
    friend bool operator == (bign a, bign b)
    {
        if (a._m != b._m) return false;
        for (int i = ; i <= a._m; i++)
            if (a._arr[i] != b._arr[i]) return false;
        return true;
    }
};

pair<ll,ll> trans(ll *a,ll m,ll k ) {//采用a置换,m为需要置换的数，k为m置换的终点,返回循环次和圈的大小
    ll num = ;//num为从m到k的循环次数，不存在则为-1
    ll tmp = m;
    while (tmp!=k) {
        if (num !=  && tmp == m) { num = -; break; }
        num++;
        tmp = a[tmp];
    }
    if (num == -)return make_pair(-, );
    int loop = ;
    while () {
        if (loop !=  && tmp == k) { break; }
        loop++;
        tmp = a[tmp];
    }
    return make_pair(num,loop);
}

ll gcd(ll a,ll b) {
    if (b == )return a;
    return gcd(b, a%b);
}

ll extgcd(ll a,ll b,ll &x,ll &y) {
    if (b == ) {
        x = ; y = ;
        return a;
    }
    ll ans = extgcd(b,a%b,x,y);
    ll tmp = x;
    x = y;
    y = tmp - a / b*y;
    return ans;
}
ll mod_inverse(ll a,ll m) {
    ll x, y;
    extgcd(a,m,x,y);
    return (m + x%m) % m;
}

pair<ll, ll>linear_congruence(const ll *A,const ll *B,const ll*M,const int& num) {
    ll x = ,m = ;
    for (int i = ; i < num;i++) {
        ll a = A[i] * m, b = B[i] - A[i] * x, d = gcd(M[i], a);
        if (b%d != )return make_pair(, -);
        ll t = b / d*mod_inverse(a / d, M[i] / d) % (M[i] / d);
        x = x + m*t;
        m *= M[i] / d;
    }
    return make_pair((x%m+m)%m, m);
}

ll d;
ll a[N_MAX], b[N_MAX];
bign k, m;
ll kd[N_MAX], md[N_MAX];//存储k和m的D进制形式
ll A[N_MAX], B[N_MAX], M[N_MAX];
int main() {
    while(scanf("%lld",&d)&&d!=-) {
        for (int i = ; i < d;i++)scanf("%lld",&a[i]);
        for (int i = ; i < d;i++)scanf("%lld",&b[i]);
        cin >> m >> k;
        int num = ;
        while (!(m==)) {
            md[num++] = m%d;
            m =m/ d;
        }
        int num2 = ;
        while (!(k == )) {
            kd[num2++] = k%d;
            k = k / d;
        }
        if (num != num2) { puts("NO"); continue; }
        pair<ll, ll>P;
        bool flag = ;
        for (int i = ; i < num-;i++) {
            P = trans(b,md[i],kd[i]);
            if (P.first == -) { puts("NO"); flag = ; break; }
            A[i] = , B[i] = P.first, M[i] = P.second;
        }
        if (flag)continue;

        P = trans(a, md[num - ], kd[num - ]);
        if (P.first == -) { puts("NO"); continue; }
        A[num - ] = , B[num - ] = P.first, M[num - ] = P.second;
        P = linear_congruence(A,B,M,num);
       if(P.second==-) { puts("NO"); continue; }
       else printf("%lld\n",P.first);
    }
    return ;
}