用前序和中序重建二叉树 python

程序实现了用二叉树的前序遍历序列和中序遍历序列重建二叉树，代码用python实现。

首先定义二叉树节点的类：

 class TreeNode:
     def __init__(self, x):
         self.val = x
         self.left = None
         self.right = None

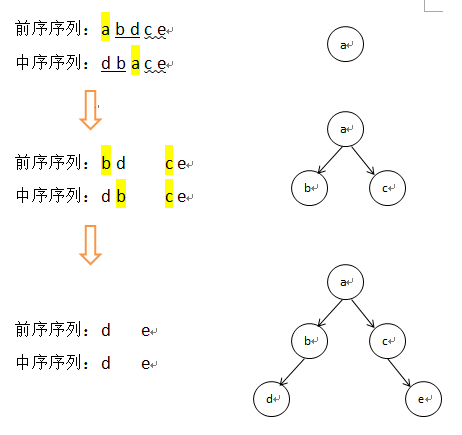
二叉树的前序遍历顺序为：根-左-右，中序遍历顺序为：左-根-右，因此可以根据前序序列准确地找到根节点，找到根节点之后，可以在中序序列中根据根节点的位置，区分出左右子树的集合，分别列出左右子树的前序序列和中序序列，然后重复这些操作，直到找到叶子结点，整个过程如下图所示。重建是相同的操作在不同的子树上重复执行的过程，因此代码利用递归完成。

 class Solution:
     def reConstructBinaryTree(self, pre, tin):#pre、tin分别是前序序列和中序序列
         # write code here
         if len(pre)>0:
             root=TreeNode(pre[0])#前序序列的第一个肯定是当前子树的根节点
             rootid=tin.index(root.val)#通过根节点在中序序列中的位置划分出左右子树包含的节点
             root.left=self.reConstructBinaryTree(pre[1:1+rootid],tin[:rootid])#重建左子树
             root.right=self.reConstructBinaryTree(pre[1+rootid:],tin[rootid+1:])#重建右子树
             return root

可以采用层序输出的方式验证生成的二叉树是否正确，用先进先出的队列依次保存层序遍历到的节点（该方法在类Solution下），然后遍历每个节点的左子节点和右子节点，代码实现如下

def PrintFromTopToBottom(self, root):
        ans=[]
        if root==None:
            return ans
        else:
            q=[root]
            while q:
                node=q.pop(0)
                ans.append(node.val)
                if node.left:
                    q.append(node.left)
                if node.right:
                    q.append(node.right)
            return ans

python版本：3.6