BZOJ 1257 - 余数之和 - [CQOI2007]

题目链接：https://www.lydsy.com/JudgeOnline/problem.php?id=1257

题意：

给定正整数 $n,k$，求 $(k \bmod 1) + (k \bmod 2) + \cdots + (k \bmod n) = \sum_{i=1}^{n}(k \bmod i)$ 的值。

题解：

显然 $k \bmod i = k - \lfloor k/i \rfloor \times i$，因此 $\sum_{i=1}^{n}(k \bmod i) = \sum_{i=1}^{n}(k - \lfloor k/i \rfloor \times i) = n \cdot k - \sum_{i=1}^{n}(\lfloor k/i \rfloor \times i)$。

对于任意正整数 $x \in [1,k]$， 设 $g(x) = \lfloor \frac{k}{\lfloor k/x \rfloor} \rfloor$，不难得出 $\lfloor k/x \rfloor \le k/x \Rightarrow \frac{k}{\lfloor k/x \rfloor} \ge \frac{k}{k/x} \Rightarrow \lfloor \frac{k}{\lfloor k/x \rfloor} \rfloor \ge \lfloor \frac{k}{k/x} \rfloor$，即 $g(x) \ge \lfloor \frac{k}{k/x} \rfloor = \lfloor x \rfloor = x$。

又根据 $f(x) = \frac{k}{x}$ 是一个单调递减函数，得到

$f(g(x)) \le f(x) \Rightarrow \frac{k}{g(x)} \le \frac{k}{x} \Rightarrow \lfloor \frac{k}{g(x)} \rfloor \le \lfloor \frac{k}{x} \rfloor$

另一方面，根据 $g(x) \le \frac{k}{\lfloor k/x \rfloor}$ 还能得出

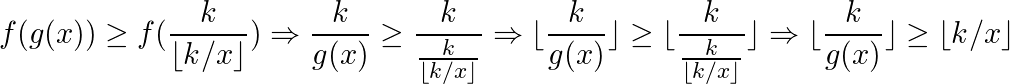
因此，综上可以得出 $\lfloor \frac{k}{g(x)} \rfloor = \lfloor \frac{k}{x} \rfloor$；也就是说，对于任意的正整数 $i \in [x,g(x)]$，$\lfloor \frac{k}{i} \rfloor$ 都是相等的。

而与此同时，对于任意的正整数 $i \in [1,k]$，$\lfloor \frac{k}{i} \rfloor$ 的值最多只有 $2 \sqrt{k}$ 个，这是因为：

当 $i \le \sqrt{k}$ 时，$i$ 最多只有 $\sqrt{k}$ 个选择，相对应地，$\lfloor \frac{k}{i} \rfloor$ 也就最多 $\sqrt{k}$ 个值；而当 $i > \sqrt{k}$ 时，$\lfloor \frac{k}{i} \rfloor \le \frac{k}{i} < \sqrt{k}$，即 $\lfloor \frac{k}{i} \rfloor$ 只能取 $1 \sim \sqrt{k}$ 之间的值。

所以，对于任意的正整数 $i \in [1,k]$，$\lfloor \frac{k}{i} \rfloor$ 的值划分成 $O(\sqrt{k})$ 段。每一段上 $i \in [x,g(x)]$，$\lfloor \frac{k}{i} \rfloor$ 的值都等于 $\lfloor \frac{k}{x} \rfloor$。而在这一段中，$\sum_{i=x}^{g(x)}(\lfloor k/i \rfloor \times i) = \lfloor k/x \rfloor \sum_{i=x}^{g(x)}i$，即一个等差数列的求和。因此这个算法时间复杂度为 $O(\sqrt{k})$。

AC代码：

/**************************************************************
    Problem: 1257
    User: Dilthey
    Language: C++
    Result: Accepted
    Time:20 ms
    Memory:1288 kb
****************************************************************/

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

ll n,k,ans;
inline ll g(ll x){return k/(k/x);}
inline ll sum(ll L,ll R){return (L+R)*(R-L+)/;}
int main()
{
    while(cin>>n>>k)
    {
        ll ans=n*k;
        n=min(n,k);
        for(ll x=;x<=n;x=g(x)+)
        {
            ll y=min(g(x),n);
            ans-=(k/x)*sum(x,y);
        }
        cout<<ans<<endl;
    }
}