清北学堂2019NOIP提高储备营DAY1

今天是第二次培训的第一天，关于NOIP的基础算法，主要内容如下：

$1.枚举

$2.搜索

$3.贪心

$1.枚举：

　　•定义：

　　　　枚举又叫做穷举，是一种基础的算法，其思路主要是：从问题中有可能的解集中一一列举出可能的解，再使用各种奇奇怪怪的方式将正确的答案找出

　　（接下来做几道题玩玩咯）

　　•例（1）

　　　　题目：一棵苹果树上长有n个苹果，每个苹果距离地面的高度用A_i来表示，小明的身高为h，试编一个程序求出小明最多能摘掉几个苹果。

　　　　分析：其实也么啥好分析的，就是将小明的身高和苹果的高度进行比较，如果苹果的高度小于小明的身高，那么小明就又能摘掉一个苹果啦！

　　　　核心代码归纳

     scanf("%d%d",&n,&h);
     for(int i=;i<=n;++i)
     {
         scanf("%d",A[i]);
         if(A[i]<h) ans++;//这里就是将汉语翻译为C++，写在一个循环里比较方便
     }        

　　•例（2）

　　　　题目：给出一个数n，判断这个数是否为素数；

　　　　分析：利用枚举的思想，枚举2到n-1中所有的数，用每个数去除以n，如果发现一个数能整除n，就说明n为合数；如果没有一个数能整除n就说明n为素数；

　　　　核心代码归纳：

 　　bool pan_su_shu(int n)
 　　{
     　　for(int i=;i<=n-;+i++)
     　　{
         　　if(n%i==) return ;//如果为合数，就不是素数
    　　 }
     　　return ;//如果为素数，就是素数
 　　}

　　　　buuuuuuuut，这个算法不能处理素数表的问题，那么就需要几个优化：

　　　　优化一：

　　　　　　埃拉托色尼筛法，具体来说就是将枚举的数字数目大大减少，只需要枚举到√n就可以得出答案

     bool pan_su_shu(int n)
     {
         for(int i=;i<=sqrt(n);+i++)
         {
             if(n%i==) return ;
         }
         return ;
     }

　　　　优化二：

　　　　　　线性筛（详见素数筛法），复杂度是线性的；

　　　　优化三：

　　　　　　miller_rubbin素性检测，详见上面的博文QAQ

$2.搜索：

　　•分类：

　　　　（1）深度优先搜索

　　　　（2）广度优先搜索

　　•深度优先搜索（DFS）　　

　　　　核心思想：深度优先搜索的核心思想就是运用递归，将所有元素进行搜索，如果满足条件或者根本无法满足条件，就返回至上一个分叉点，选择另一条路径，再次搜索

　　•广度优先搜索（BFS）

　　　　核心思想：广度优先搜索的核心思想就是运用队列，将每个分叉节点的几个可能的存在存在队列里，对队列进行搜索，从而完成整个搜索

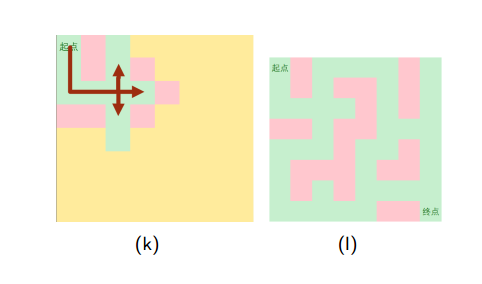
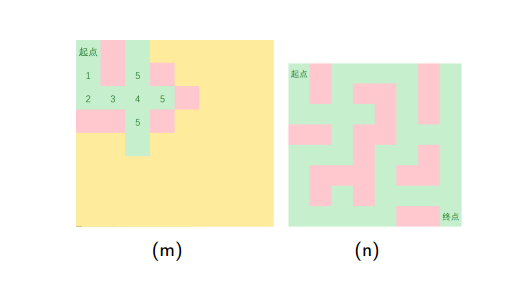
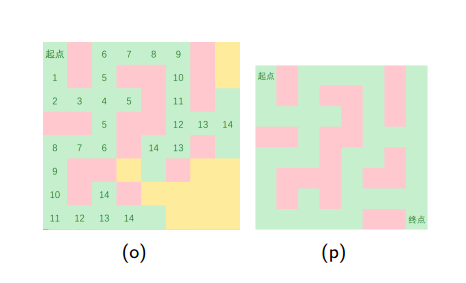
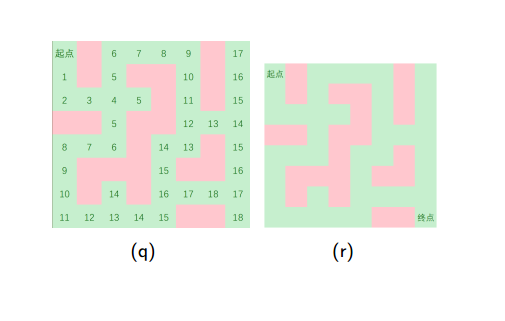
　　•以迷宫问题为例，用图来表示一下BFS和DFS的区别（by冯哲大神的PPT）

　　　　下面是深度优先搜索的图示：

　　

　　

　　　　下面是广度优先搜索的图示：

　　

　　

　　

　　

　　

　　　　这样就差不多了，继续继续

　　

　　•总结：

　　　　深度优先搜索的优点：代码短，占用空间少

　　　　　　　　　　　缺点：找到的不一定是最优解，代码的复杂度很高

　　　　广度优先搜索的优点：保证找到的解一定是最优解，复杂度低

　　　　　　　　　　　缺点：代码较长（不好背），占空间大，需要维护一个当前指向的集合（队列）

　　　　两种搜索各有利弊，有时在复杂度或空间的要求下，只能选取最优的，这时就需要对两种方式进行取舍。在NOIP的考试中，一定要进行正确的选择！！！

　　•深度优先搜索的例题：

　　　　八数码游戏：这个游戏大概是这样的----给你一个3*3的九宫格图，里面有1-8八个数字和0。0代表没有数字。你需要做的就是通过这个0，将其他的数字移动成以下局面：

　　　　　　　　1　　2　　3

　　　　　　　　4　　5　　6

　　　　　　　　7　　8　　0

　　　　求该操作的最小步数

　　　　思路浅析：这道题用的是BFS，具体思路是将每一次操作都进行一次转移-->转移成这个情况下可能到达的情况，最后就会到达目标情况，也就会求出最小步数

　　　　代码实现就不打了，今天就只做思路的浅析

　　•广度优先搜索的例题：

　　　　戳这里！！！（讲的是队列和广度优先搜索的例题）

$3.贪心

　　•啥是贪心？

　　　　简单来说，贪心就是一种每一步都选取局部最优解的算法。这种算法一般都符合直观思路，但是使用的话需要严格的证明，这就是为什么在NOIP中要对贪心算法的使用进行斟酌。但是如果有的毒瘤题实在不会，可以尝试用贪心算法骗个一两分

　　•贪心的例题：

　　　　例（1）：

　　　　给定有n个农民，每个农民手中都有Ai个单位的牛奶，单价为pi，现在给你一个任务，要求你从这些农民手中买下m单位的牛奶，最省钱的方案为？

　　　　思路：这提是最简单的贪心算法，将么个农民手中牛奶的单价按从小到大的顺序排序，从最小单价的农民手中买牛奶，直到达到m单位

　　　　例（2）;

　　　　有n个物品，每个物品都有Ai和Bi两个属性，现在将这n个物品按照某种方式排序，但是每个物品排序都有不同的代价，代价的计算公式如下：

　　　　假设第i个物品被放在了第j个位置，那么这个物品所需的代价为Ai*（j-1）+Bi*（n-j）

　　　　试编写一个程序，算出最小的代价

　　　　思路：对于这种计算公式的题目，有可能存在一个最小值，需要用贪心求解。这里介绍一个技巧：可以先将公式展开再化简，也就是将这个式子换一个方式来表示，有可能看出贪心的方法。对于这道题，我们可以将原式拆开，得到ans = ΣAi · j - Ai + Bi · n - Bi · j

　　　　这样，我们就可以发现，ΣBi*n-Ai是一个常数，变化的只有Σ（Ai-Bi）*j，那么就可以将Ai-Bi进行从大到小的排序，每次取最大的值（因为j会增大），这样就解粗来了！

see you tomorrow（金针菇）

　　　　

引用资料：

　　冯哲大神的PPT