简单理解 SVM

SVM，中文名叫支持向量机。

在深度学习出现以前，它是数据挖掘的宠儿；

SVM具有十分完整的数据理论证明，但同时理论也相当复杂。

初识SVM 

同其他分类算法一样，SVM分类也是寻找合适的决策边界，为方便理解，以二分类为例。

假设存在二分类样本，我们一定可以找到一个超平面将类别分开，但是通常会存在很多这样的超平面。

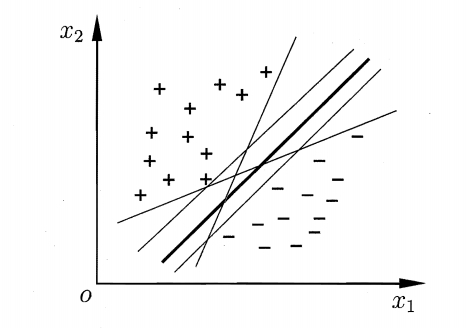
那取哪个呢？

直观感受

直观来看，应该取中间那条粗线，因为这条线对样本的“容忍性”最好，也就是说样本发生微小变化，不会影响分类结果，但是其他细线，如果样本发生微小变化，都会使得分类结果发生变化，也就是说粗线作为决策边界，其鲁棒性最好。

数学解释

从直观上看，取粗线为宜，但是这条粗线有很多的平行线，都可以实现分类，那么怎么取呢？

我们把这条粗线向两边平移，直至粗线和两边离他最近的样本重合，此时生成了2个新的超平面，记为 b11，b12，然后我们可以把之前的粗线移动到b11和b12的中间，确保粗线到b11和b12的距离相等

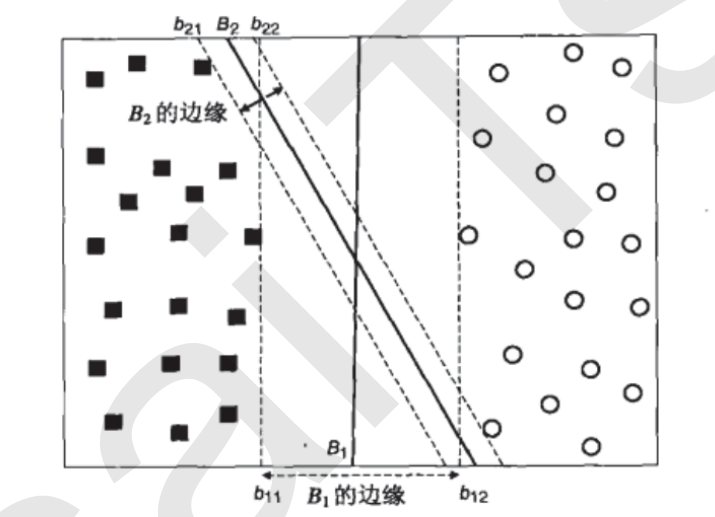
假设我们有两条粗线B1，B2，分别完成上述操作，

b11和b12之间的距离，叫做B1这条决策边界的边际（margin），也有叫“间隔”，记为d，当然也有把b11和B1的距离叫边际的，无所谓，不影响理论

显然拥有更大的边际的决策边界泛化能力更强

与b11和b12相交的样本点叫支持向量

数学建模

如何找到具有最大边际的决策边界呢？

假设这个超平面为 wx+b=0

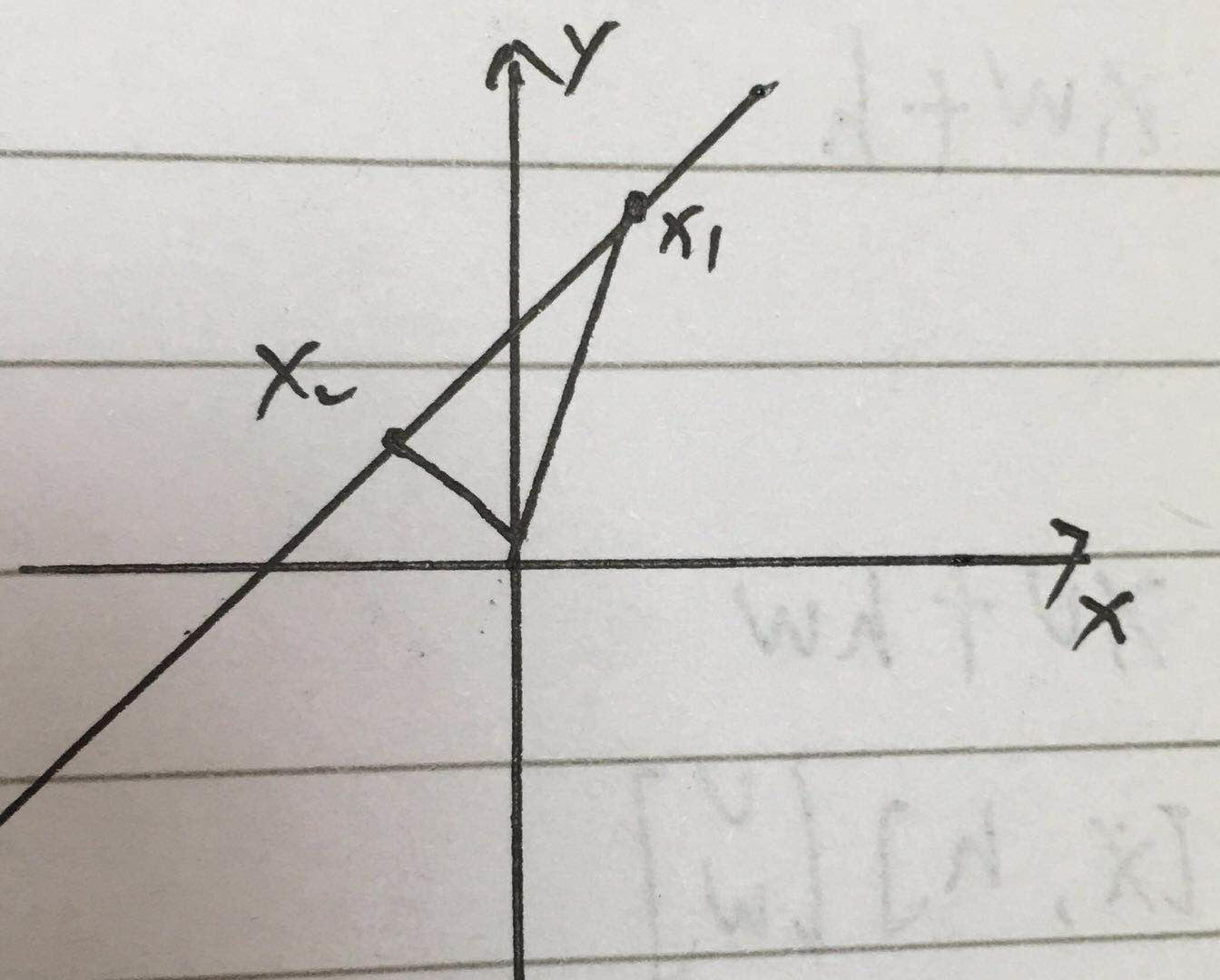
超平面上取两点x1，x2，则

wx1+b=0

wx2+b=0

w(x1-x2)=0，故w与x1-x2垂直，即w为超平面的法向量。

超平面外任意点到平面的距离为

此时把支持向量带入上式，即可得到

d=2r，带有绝对值，不好处理。

解释

1. 上图把超平面的表达形式稍微变化了一下，而且进行了一系列的推导

2. 其实最开始也有解释，如果向两侧平移不同距离，那么应该先调整决策边界到两个新平面的中间，此时3个平面的wb都要做调整。

3. 上图是许多资料未讲明的地方

4. 上图是个变换过程，如果二分类的标签不是-1 1，也可以变换成-1 1

上图的结论是

假设是二分类，那么决策边界 wx+b=0 向两侧平移1，可得

等号成立的条件就是支持向量，此时 |wx+b|=1，那么

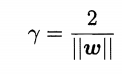
这就是边际d。

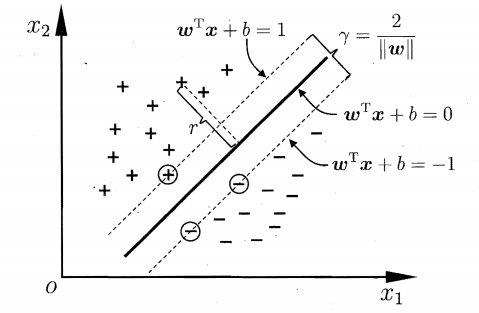
欲使边际最大，就是 maxd

注意，在训练过程中，我们使用的是全部样本，而不单是支持向量，而全部样本存在约束

综合表示就是 y(wx+b)>1,

那么目标为

最大转换为最小，方便计算

w加了平方，也是方便计算，不影响，w最小，w平方也就最小

以上就是SVM的基础理论。

拉格朗日乘子与对偶问题

其实上面的目标函数已经是个凸函数，可以用梯度下降等优化算法来求解，但是SVM使用了另一种优化算法，即拉格朗日对偶函数，

这部分比较麻烦，如果你不是专门研究SVM，没必要太纠结这块，因为即使你弄明白了，过一段时间就会忘记。

核函数

上面讲到用超平面来划分样本，但现实中很多问题是线性不可分的，此时不存在可划分类别的超平面。

对于这样的问题，需要将样本从原始空间映射到一个更高维的空间，使得样本在新的特征空间线性可分。

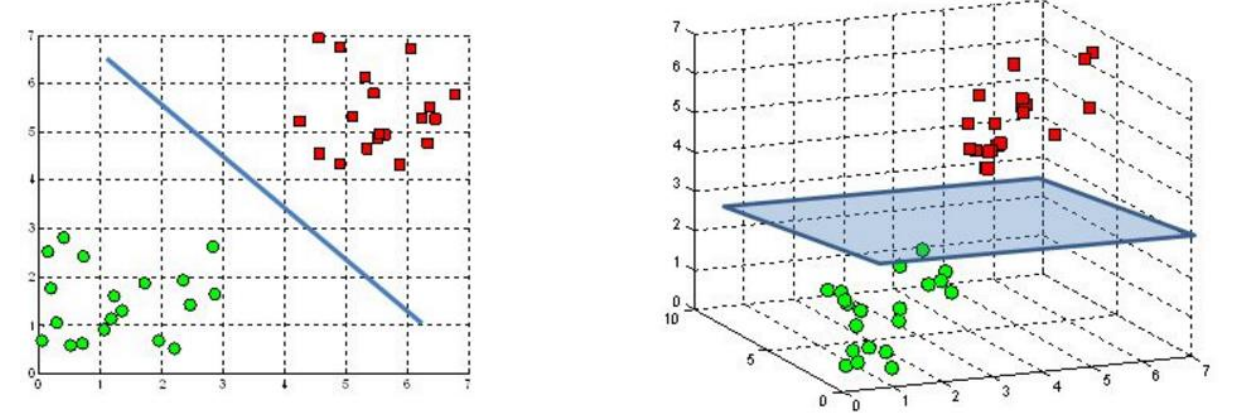
如果原始空间有限，那么一定存在一个高维空间使得样本可分。

这种映射其实就是一个函数，我们称之为核函数。

常用的核函数有

　

一般情况下会先用高斯核试试，但经验告诉我们，文本一般使用线性核。

核函数的计算也是可以简化的

软间隔与正则化

SVM总是在寻找超平面使得样本能够完全被分开，但是由于现实中数据杂质很多，完全分开很容易造成过拟合。

缓解这个问题的思路就是允许部分样本被错误划分，于是提出了“软间隔”的概念（相对有“硬间隔”的概念）

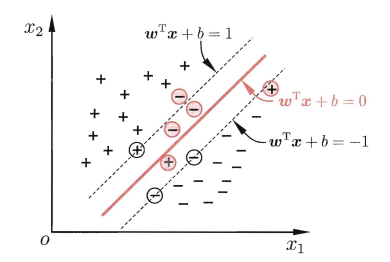
可以看到红色样本被错误划分

此时的红色样本实际为1（-1），预测为-1（1），已经不满足 y(wx+b)>1的约束条件，

那对应我们的目标函数怎么改呢？去掉约束吗？显然不能

在分类时，我们虽然容忍部分样本被错误划分，但是我们希望被错误划分的样本越少越好，也就是说我们希望大部分样本仍然满足约束条件。

目标函数可改为

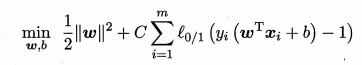
C是个>0的常数，也就是正则项系数，这里叫容忍系数

l_0/1是“0/1损失函数”

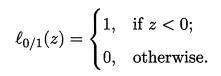
当样本被错误分类时，y(wx+b)<0，y(wx+b)-1<0，l_0/1=1，

当样本被正确分类时，l_0/1=0

要使目标函数最小，就要使后面那部分最小，然而当样本被错误划分时，后面为1，如果C很大，那么后面那部分就很大，显然不符合我们的目标，所以需要1尽可能少，也就是错误划分尽可能少。

当C无穷大时，就是不能错误划分，后面那部分是0，目标函数最小，也就是“硬间隔”。

所以C越大，模型越“精确”。

由于l_0/1函数非凸，非连续，数学性质不太好，所以要用其他函数来替代它，称为“替代损失”

三种常用的替代损失函数

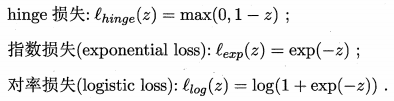
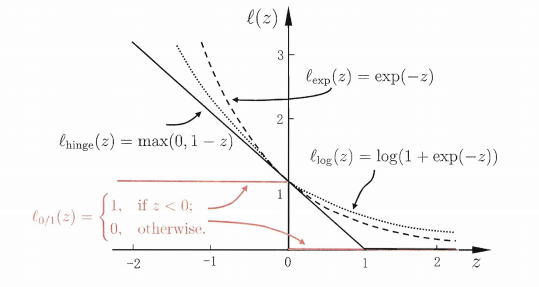
总结

SVM的理论十分复杂，上面只是介绍了冰山一角，有助于你在实际项目中完成调参工作。

参考资料：

周志华 《机器学习》