【bzoj4543】Hotel加强版（thr）

Portal --> bzoj4543

Solution

​　　一年前的题== 然而一年前我大概是在划水qwq

​​　　其实感觉好像关键是。。设一个好的状态？然后。。你要用一种十分优秀的方式快乐转移qwq

​　　

​​　　首先是状态，我们设\(f[x][i]\)表示以\(x\)为根的子树中，与\(x\)的距离为\(i\)的节点数量，\(g[x][i]\)表示。。\(x\)子树内形如下图的点对\((a,b)\)（无序）的数量

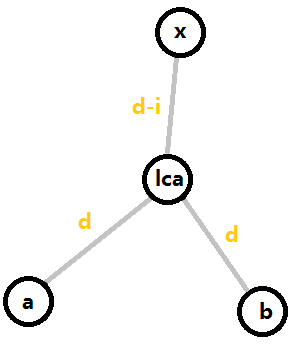
​​　　其中\(d\)是一个。。不确定的值（说白了就是所有的\(d\)都要考虑到），或者更加直白地说，只要在\(x\)节点上“接上”一条长度为\(i\)的边（边连着一个节点\(y\)），那么\(y,a,b\)可以构成一个满足题目要求的方案

​​　　然后这个时候我们就可以快乐转移了，枚举\(x\)的后继\(u\)：

\[\begin{aligned}
g[x][i]&+=f[x][i]*f[u][i-1]+g[u][i+1]\\
f[x][i]&+=f[u][i-1]\\
\end{aligned}
\]

​​　　其中\(i\)的范围都是\(1\sim\)子树内的最大深度

​​　　稍微解释一下\(g\)的转移：前面的乘法的话就是\(lca\)为\(x\)的情况，后面的话就是从子树中直接继承上来（注意\(+1\)的话是因为\(i\)是被减的那个量）

​​　　接下来是答案的统计，考虑统计经过\(x\)的方案，我们有：

\[ans+=\sum\limits_{u\in son(x)}f[u][i-1]*g[x][i]+g[u][i]*f[x][i-1]
\]

​​　　同样的\(i\)的范围也是\(1\sim\)子树内的最大深度

​​　　那么这个时候可能会有疑问，接上去的那个点的连边不能是一个带“折”的边吗，为什么可以直接用不带折的\(f\)算呢？其实稍微画一下图：

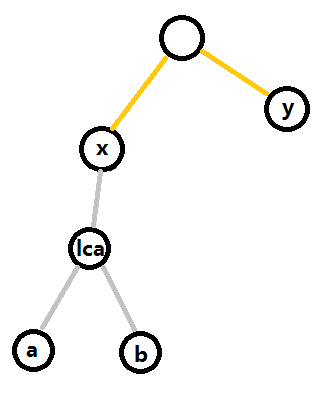
​​　　（注意图中的一条边。。可能是一条链只是我懒得画了qwq）我们会发现这种情况其实会在统计图中那个没有标号的节点的时候统计到（没有标号的节点的\(g\)中是可能包含了\((a,b)\)这种情况的（如果他们可能构成一种合法方案的话），然后这个时候\(y\)这个节点其实就是\(f\)中的一部分，所以如果可能构成合法方案的话是会被算进空白节点的贡献中的

​​　　（所以说其实。。也不能够叫做统计经过\(x\)的方案的答案）

​　　

​　　然后现在的问题就是我们怎么快速转移

​​　　发现那个\(i\)的变化很有规律，考虑当我们在树形dp中将第一个儿子的值拿来更新父亲的时候的情况，稍微写一下大概是这样：

\[\begin{aligned}
f[x][i]&=f[u][i-1]\\
g[x][i]&=g[u][i+1]\\
\end{aligned}
\]

​​　　我们将\(f[x],g[x],f[u],g[u]\)都看成一个整体的话，\(f[u]\)到\(f[x]\)的转移其实相当于整体向前或向后偏移了一位，\(g[x]\)和\(g[u]\)的转移也是一样，所以我们其实可以用指针（或者。。下标偏移一下什么的，我的代码写的就是这个因为我不太会用指针qwq）来实现\(O(1)\)的转移

​​　　然后对于后面的情况我们都要老老实实枚举\(i\)，因此转移复杂度是跟\(u\)的子树最大深度相关的

​​　　所以我们不妨考虑把子树最大深度最大的那个后继钦定为第一个后继，\(O(1)\)转移它的信息，然后其他的后继就\(O(dep)\)转移（其实就是长链剖分一下qwq把重儿子摆在一起），这样的话就能够做到整体复杂度\(O(n)\)了（证明的话我不是很会qwq网上看到dalao的博客中说的貌似是直接用深度相减算出一个点的转移的复杂度然后求一下和发现除了叶子节点以外的所有点的\(dep\)都被抵消了所以就是\(O(n)\)了）

​​　　然后再稍微说一下下标偏移写法的实现：具体一点就是我们考虑将所有的\(f\)的值排成一排（\(g\)的值也是一样），像树链剖分中的线段树一样将一条长链中所有的节点的信息放在连续的一段，链上的转移的话\(f\)相当于每次往后移一位，\(g\)相当于每次往前移一位（因此在存的时候一条链预留的长度应该\(*2\)，因为要预留往前移的空间）

​​　　转移的时候一定要注意边界。。。

​　　

​​　　代码大概长这个样子

#include<iostream>
#include<cstdio>
#include<cstring>
#define ll long long
using namespace std;
const int N=5*(1e5)+10;
struct xxx{
	int y,nxt;
}a[N*2];
int h[N],dep[N],top[N],mx[N],son[N],pre[N],pos[N];
int dfn[N];
ll f[N*10],g[N*10];
int n,m,tot,dfn_t,lis_pos;
ll ans;
void add(int x,int y){a[++tot].y=y; a[tot].nxt=h[x]; h[x]=tot;}
void dfs(int fa,int x,int d){
	int u;
	dep[x]=d; mx[x]=1;
	pre[x]=fa; son[x]=0;
	for (int i=h[x];i!=-1;i=a[i].nxt){
		u=a[i].y;
		if (u==fa) continue;
		dfs(x,u,d+1);
		mx[x]=max(mx[x],mx[u]+1);
		if (mx[son[x]]<mx[u]+1) son[x]=u;
	}
}
void dfs1(int fa,int x){
	int u;
	dfn[x]=++dfn_t;
	if (son[x]){
		top[son[x]]=top[x];
		dfs1(x,son[x]);
	}
	for (int i=h[x];i!=-1;i=a[i].nxt){
		u=a[i].y;
		if (u==fa||u==son[x]) continue;
		top[u]=u; pos[u]=lis_pos+mx[u];
		lis_pos+=mx[u]*2;
		dfs1(x,u);
	}
}
int locf(int x,int i){return dfn[x]+i;}
int locg(int x,int i){return pos[top[x]]-(dep[x]-dep[top[x]])+i;}
int calc(int x,int u){
	for (int i=1;i<=mx[u];++i)
		ans+=f[locf(u,i-1)]*g[locg(x,i)];
	for (int i=1;i<mx[u];++i)
		ans+=g[locg(u,i)]*f[locf(x,i-1)];
	for (int i=0;i<mx[u]-1;++i)
		g[locg(x,i)]+=g[locg(u,i+1)];
	for (int i=1;i<=mx[u];++i){
		g[locg(x,i)]+=f[locf(x,i)]*f[locf(u,i-1)];
		f[locf(x,i)]+=f[locf(u,i-1)];
	}
}
void solve(int fa,int x){
	int u;
	if (!son[x]){
		f[locf(x,0)]=1; g[locg(x,0)]=0;
		return;
	}
	solve(x,son[x]);
	g[locg(x,mx[x])]=g[locg(x,mx[x]-1)]=0;
	ans+=g[locg(x,0)];
	f[locf(x,0)]=1;
	for (int i=h[x];i!=-1;i=a[i].nxt){
		u=a[i].y;
		if (u==fa||u==son[x]) continue;
		solve(x,u);
		calc(x,u);
	}
}
void init(){
	memset(h,-1,sizeof(h));
	tot=0;
	memset(f,0,sizeof(f));
	memset(g,0,sizeof(g));
}

int main(){
#ifndef ONLINE_JUDGE
	freopen("a.in","r",stdin);
#endif
	int x,y;
	while (1){
		scanf("%d",&n);
		if (!n) return 0;
		init();
		for (int i=1;i<n;++i){
			scanf("%d%d",&x,&y);
			add(x,y); add(y,x);
		}
		dfs(0,1,1);
		dfn_t=0; lis_pos=0;
		top[1]=1; pos[1]=lis_pos+mx[1];
		lis_pos=mx[1]*2;
		dfs1(0,1);
		ans=0;
		solve(0,1);
		printf("%lld\n",ans);
	}
}