【转】二叉树、B树、B-树、B+树、B*树

二叉树

1.所有非叶子结点至多拥有两个儿子（Left和Right）；

2.所有结点存储一个关键字；

3.非叶子结点的左指针指向小于其关键字的子树，右指针指向大于其关键字的子树；

如：

二叉树的搜索，从根结点开始，如果查询的关键字与结点的关键字相等，那么就命中；

否则，如果查询关键字比结点关键字小，就进入左儿子；如果比结点关键字大，就进入

右儿子；如果左儿子或右儿子的指针为空，则报告找不到相应的关键字；

如果二叉树的所有非叶子结点的左右子树的结点数目均保持差不多（平衡），那么二叉树

的搜索性能逼近二分查找；但它比连续内存空间的二分查找的优点是，改变二叉树结构

（插入与删除结点）不需要移动大段的内存数据，甚至通常是常数开销；

如：

但二叉树在经过多次插入与删除后，有可能导致不同的结构：

右边也是一个二叉树，但它的搜索性能已经是线性的了；同样的关键字集合有可能导致不同的

树结构索引；所以，使用二叉树还要考虑尽可能让二叉树保持左图的结构，和避免右图的结构，也就

是所谓的“平衡”问题；

实际使用的二叉树都是在原二叉树的基础上加上平衡算法，即“平衡二叉树”；如何保持二叉树

结点分布均匀的平衡算法是平衡二叉树的关键；平衡算法是一种在二叉树中插入和删除结点的

策略；

 B树

1970年，R.Bayer和E.mccreight提出了一种适用于外查找的树，它是一种平衡的多叉树，称为B树（或B-树、B_树）。

一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树。它或者是空树，或者是满足下列性质的树：

1、根结点至少有两个子女；

2、每个非根节点所包含的关键字个数 j 满足：┌m/2┐ - 1 <= j <= m - 1；

3、除根结点以外的所有结点（不包括叶子结点）的度数正好是关键字总数加1，故内部子树个数 k 满足：┌m/2┐ <= k <= m ；

4、所有的叶子结点都位于同一层。

在B-树中，每个结点中关键字从小到大排列，并且当该结点的孩子是非叶子结点时，该k-1个关键字正好是k个孩子包含的关键字的值域的分划。

因为叶子结点不包含关键字，所以可以把叶子结点看成在树里实际上并不存在外部结点，指向这些外部结点的指针为空，叶子结点的数目正好等于树中所包含的关键字总个数加1。

B-树中的一个包含n个关键字，n+1个指针的结点的一般形式为： （n,P0,K1,P1,K2,P2,…,Kn,Pn）

其中，Ki为关键字，K1<K2<…<Kn, Pi 是指向包括Ki到Ki+1之间的关键字的子树的指针。

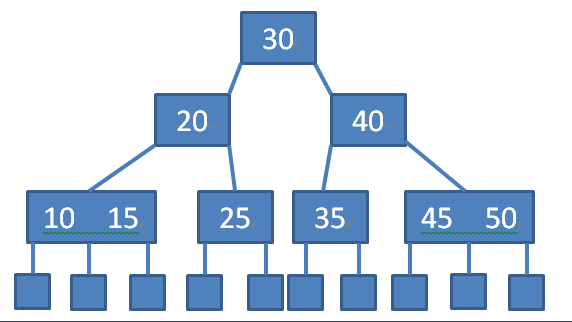
B-树

是一种多路搜索树（并不是二叉的）：

1.定义任意非叶子结点最多只有M个儿子；且M>2；

2.根结点的儿子数为[2, M]；

3.除根结点以外的非叶子结点的儿子数为[M/2, M]；

4.每个结点存放至少M/2-1（取上整）和至多M-1个关键字；（至少2个关键字）

5.非叶子结点的关键字个数=指向儿子的指针个数-1；

6.非叶子结点的关键字：K[1], K[2], …, K[M-1]；且K[i] < K[i+1]；

7.非叶子结点的指针：P[1], P[2], …, P[M]；其中P[1]指向关键字小于K[1]的

子树，P[M]指向关键字大于K[M-1]的子树，其它P[i]指向关键字属于(K[i-1], K[i])的子树；

8.所有叶子结点位于同一层；

如：（M=3）

B-树的搜索，从根结点开始，对结点内的关键字（有序）序列进行二分查找，如果

命中则结束，否则进入查询关键字所属范围的儿子结点；重复，直到所对应的儿子指针为

空，或已经是叶子结点；

B-树的特性：

1.关键字集合分布在整颗树中；

2.任何一个关键字出现且只出现在一个结点中；

3.搜索有可能在非叶子结点结束；

4.其搜索性能等价于在关键字全集内做一次二分查找；

5.自动层次控制；

由于限制了除根结点以外的非叶子结点，至少含有M/2个儿子，确保了结点的至少

利用率，其最底搜索性能为：

其中，M为设定的非叶子结点最多子树个数，N为关键字总数；

所以B-树的性能总是等价于二分查找（与M值无关），也就没有B树平衡的问题；

由于M/2的限制，在插入结点时，如果结点已满，需要将结点分裂为两个各占

M/2的结点；删除结点时，需将两个不足M/2的兄弟结点合并；

B+树

B+树是B-树的变体，也是一种多路搜索树：

1.其定义基本与B-树同，除了：

2.非叶子结点的子树指针与关键字个数相同；

3.非叶子结点的子树指针P[i]，指向关键字值属于[K[i], K[i+1])的子树

（B-树是开区间）；

5.为所有叶子结点增加一个链指针；

6.所有关键字都在叶子结点出现；

如：（M=3）

B+的搜索与B-树也基本相同，区别是B+树只有达到叶子结点才命中（B-树可以在

非叶子结点命中），其性能也等价于在关键字全集做一次二分查找；

B+的特性：

1.所有关键字都出现在叶子结点的链表中（稠密索引），且链表中的关键字恰好

是有序的；

2.不可能在非叶子结点命中；

3.非叶子结点相当于是叶子结点的索引（稀疏索引），叶子结点相当于是存储

（关键字）数据的数据层；

4.更适合文件索引系统；

B*树

是B+树的变体，在B+树的非根和非叶子结点再增加指向兄弟的指针；

B*树定义了非叶子结点关键字个数至少为(2/3)*M，即块的最低使用率为2/3

（代替B+树的1/2）；

B+树的分裂：当一个结点满时，分配一个新的结点，并将原结点中1/2的数据

复制到新结点，最后在父结点中增加新结点的指针；B+树的分裂只影响原结点和父

结点，而不会影响兄弟结点，所以它不需要指向兄弟的指针；

B*树的分裂：当一个结点满时，如果它的下一个兄弟结点未满，那么将一部分

数据移到兄弟结点中，再在原结点插入关键字，最后修改父结点中兄弟结点的关键字

（因为兄弟结点的关键字范围改变了）；如果兄弟也满了，则在原结点与兄弟结点之

间增加新结点，并各复制1/3的数据到新结点，最后在父结点增加新结点的指针；

所以，B*树分配新结点的概率比B+树要低，空间使用率更高；

小结

二叉树：二叉树，每个结点只存储一个关键字，等于则命中，小于走左结点，大于

走右结点；

B-树：多路搜索树，每个结点存储M/2到M个关键字，非叶子结点存储指向关键

字范围的子结点；

所有关键字在整颗树中出现，且只出现一次，非叶子结点可以命中；

B+树：在B-树基础上，为叶子结点增加链表指针，所有关键字都在叶子结点

中出现，非叶子结点作为叶子结点的索引；B+树总是到叶子结点才命中；

B*树：在B+树基础上，为非叶子结点也增加链表指针，将结点的最低利用率

从1/2提高到2/3；

【转自】http://blog.csdn.net/nashouat/article/details/8494946