STL标准库-容器-rb_tree

技术在于交流、沟通，本文为博主原创文章转载请注明出处并保持作品的完整性

红黑树,关联式容器底层实现(map set),在使用中基本运用不到,但是还是想了解一下他的运作方式

Red_Black tree是平衡二分搜寻树(balanced binary search tree),它是高度平衡的二叉树,这样有利于search和insert.

红黑树提供遍历,如果如果按正常规则(++iter)遍历,便能获得排序状态

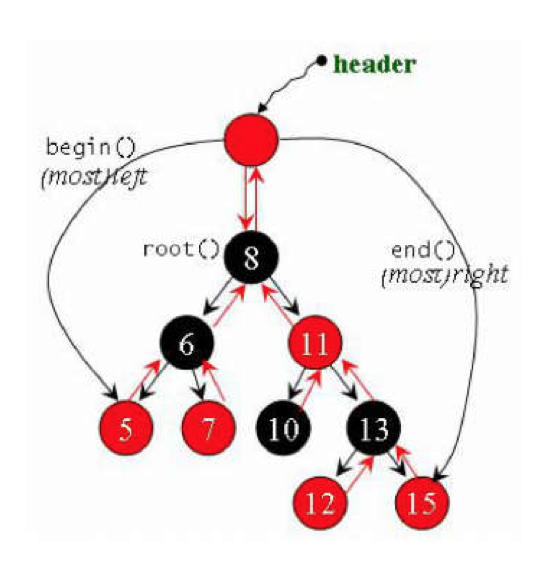
如上图,你会发现返回迭代器头的begin()函数指向的是"5"这个点.end()记录着最大点"15",它永远先走左边后走右边.

如果你遍历上面的红黑树就会得到 5,6,7,8,10,11,12,13,15

但是我们不应该使用红黑树的迭代器改变其元素,如果改变就会破坏原树的结构,但是编程的层面没有禁止(是可以改,但是我们不应该改).

因为rb_tree是为了实现set和map,而map允许元素data的改变,但是map的key不能够改变.

rb_tree提供两种insertion操作:insert_unique()[插入的key是第一无二的,否则插入失败]. insert_equal()[允许key重复] .

先说一下红黑数的基本性质

红黑树的性质：

a.每个节点或是红的,或是黑的

b.根节点是黑色的

c.每个叶节点(NULL)是黑色的

d.如果一个节点是红色的,则它的两个子节点都是黑色的

e.对每个节点,从该节点到其所有后代叶节点的简单路径上,均含有相同数目的黑色节点

---

Source Code

介绍rb_tree的部分源码

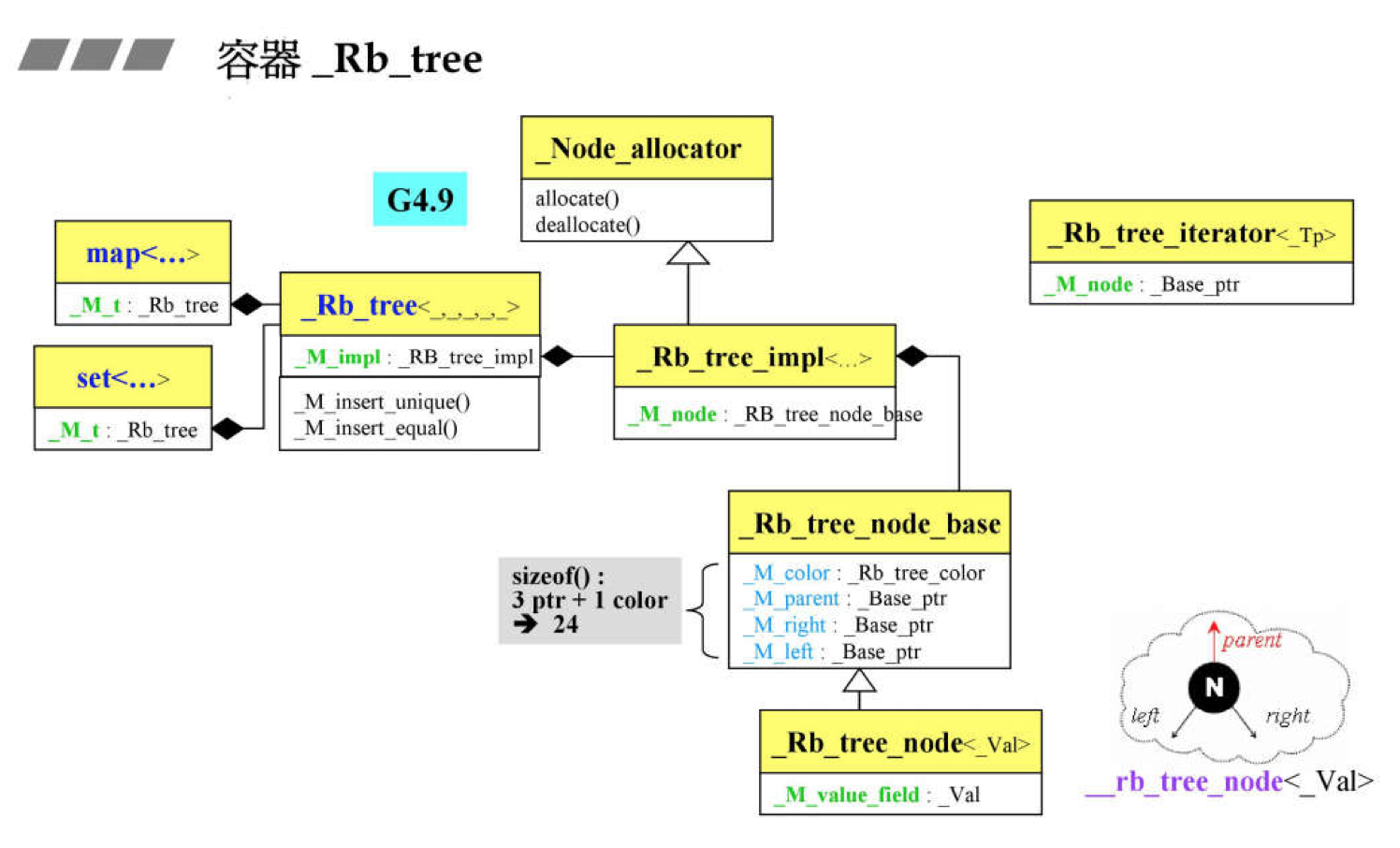
一 数据类

先看红黑树的数据类 _Rb_tree_node_base

    enum _Rb_tree_color { _S_red = false, _S_black = true };//红黑树的颜色 红色0 黑色1

    struct _Rb_tree_node_base
    {
        typedef _Rb_tree_node_base* _Base_ptr; //节点指针
        typedef const _Rb_tree_node_base* _Const_Base_ptr;//const节点指针

        _Rb_tree_color    _M_color;//颜色
        _Base_ptr        _M_parent;//父节点
        _Base_ptr        _M_left;//左节点
        _Base_ptr        _M_right;//右节点

        static _Base_ptr//最小节点,即最左节点
        _S_minimum(_Base_ptr __x) _GLIBCXX_NOEXCEPT
        {
            while (__x->_M_left != ) __x = __x->_M_left;//只要左节点不为空就一直向左走,取得最小节点
            return __x;
        }

        static _Const_Base_ptr
        _S_minimum(_Const_Base_ptr __x) _GLIBCXX_NOEXCEPT
        {
            while (__x->_M_left != ) __x = __x->_M_left;
            return __x;
        }

        static _Base_ptr//最大节点,即最右节点
        _S_maximum(_Base_ptr __x) _GLIBCXX_NOEXCEPT
        {
            while (__x->_M_right != ) __x = __x->_M_right;
            return __x;
        }

        static _Const_Base_ptr
        _S_maximum(_Const_Base_ptr __x) _GLIBCXX_NOEXCEPT
        {
            while (__x->_M_right != ) __x = __x->_M_right;
            return __x;
        }
    };

其子类_Rb_tree_node

    template<typename _Val>//红黑树的节点结构
    struct _Rb_tree_node : public _Rb_tree_node_base
    {
        typedef _Rb_tree_node<_Val>* _Link_type;//节点指针 指向数据节点

#if __cplusplus < 201103L
        _Val _M_value_field;//数据类型

        _Val*
        _M_valptr()
        { return std::__addressof(_M_value_field); }　

        const _Val*
        _M_valptr() const
        { return std::__addressof(_M_value_field); }
#else
        __gnu_cxx::__aligned_buffer<_Val> _M_storage;//对齐处理后数据

        _Val*
        _M_valptr() //返回对应数据的指针
        { return _M_storage._M_ptr(); }

        const _Val*
        _M_valptr() const
        { return _M_storage._M_ptr(); }
#endif
    };

std::_addressof()的实现在 move.h中找到其实现 用于取变量和函数的内存地址　

  template<typename _Tp>
    inline _Tp*
    __addressof(_Tp& __r) _GLIBCXX_NOEXCEPT
    {
      return reinterpret_cast<_Tp*>
    (&const_cast<char&>(reinterpret_cast<const volatile char&>(__r)));
    }

volatitle是一种类型修饰符，用它声明的类型变量表示可以被某些编译器未知的因素更改.

比如：操作系统、硬件或者其它线程等。遇到这个关键字声明的变量，编译器对访问该变量的代码就不再进行优化，从而可以提供对特殊地址的稳定访问。

声明时语法：int volatile vInt; 当要求使用 volatile 声明的变量的值的时候，系统总是重新从它所在的内存读取数据，即使它前面的指令刚刚从该处读取过数据。而且读取的数据立刻被保存

---

二 迭代器 _Rb_tree_iterator

template<typename _Tp>
    struct _Rb_tree_iterator
    {
        typedef _Tp  value_type;
        typedef _Tp& reference;
        typedef _Tp* pointer;

        typedef bidirectional_iterator_tag iterator_category; //迭代器类型
        typedef ptrdiff_t                  difference_type; //两个迭代器间距离

        typedef _Rb_tree_iterator<_Tp>        _Self;
        typedef _Rb_tree_node_base::_Base_ptr _Base_ptr;//节点指针
        typedef _Rb_tree_node<_Tp>*           _Link_type;//节点指针
        //ctor
        _Rb_tree_iterator() _GLIBCXX_NOEXCEPT
        : _M_node() { }

        explicit
        _Rb_tree_iterator(_Link_type __x) _GLIBCXX_NOEXCEPT
        : _M_node(__x) { }

        reference
        operator*() const _GLIBCXX_NOEXCEPT
        { return *static_cast<_Link_type>(_M_node)->_M_valptr(); }
        //操作符重载返回节点指针
        pointer
        operator->() const _GLIBCXX_NOEXCEPT
        { return static_cast<_Link_type> (_M_node)->_M_valptr(); }

        _Self&
        operator++() _GLIBCXX_NOEXCEPT
        {
            _M_node = _Rb_tree_increment(_M_node);//这个函数的实现在4.9中没有找到 用一下其他版本的 其实现原理基本相似
            return *this;
        }

        _Self
        operator++(int) _GLIBCXX_NOEXCEPT
        {
            _Self __tmp = *this;
            _M_node = _Rb_tree_increment(_M_node);//++操作
            return __tmp;
        }

        _Self&
        operator--() _GLIBCXX_NOEXCEPT//--也没找到
        {
            _M_node = _Rb_tree_decrement(_M_node);
            return *this;
        }

        _Self
        operator--(int) _GLIBCXX_NOEXCEPT
        {
            _Self __tmp = *this;
            _M_node = _Rb_tree_decrement(_M_node);
            return __tmp;
        }

        bool
        operator==(const _Self& __x) const _GLIBCXX_NOEXCEPT
        { return _M_node == __x._M_node; }

        bool
        operator!=(const _Self& __x) const _GLIBCXX_NOEXCEPT
        { return _M_node != __x._M_node; }

        _Base_ptr _M_node;
    };

operator++

//RB-Tree的后继点
   void _M_increment()
  {
    //the right subtree of node x is not empty
      //存在右子树，则找出右子树的最小节点
    if (_M_node->_M_right != ) {//如果有右子树
      _M_node = _M_node->_M_right;//向右边走
      while (_M_node->_M_left != )//往右子树中的左边一直走到底
        _M_node = _M_node->_M_left;//最左节点就是后继结点
    }
    //the right subtree of node x is empty,and the node of x has a successor node y
    //没有右子树，但是RB-Tree中节点node存在后继结点
    else {
      _Base_ptr __y = _M_node->_M_parent;//沿其父节点向上查找
      while (_M_node == __y->_M_right) { //若节点是其父节点的右孩子,则向上查找,
        _M_node = __y;                    //一直向上查找,直到“某节点不是其父节点的右孩子”为止
        __y = __y->_M_parent;
      }

      if (_M_node->_M_right != __y)//若此时的右子节点不等于此时的父节点
        _M_node = __y;//此时的父节点即为解答
                        //否则此时的node为解答
    }
  }

operator--

//RB-Tree的前驱节点
  void _M_decrement()
  {
    if (_M_node->_M_color == _S_rb_tree_red &&// 如果是红节点，且
        _M_node->_M_parent->_M_parent == _M_node)// 父节点的父节点等于自己
      _M_node = _M_node->_M_right;             //右子节点即为解答。
    /*
      以上情况发生于node为header时（亦即node为end()时）。注意，header之右孩子即
      mostright，指向整棵树的max节点。
      */
    else if (_M_node->_M_left != ) {//若有左孩子节点。左子树的最大值即为前驱节点
      _Base_ptr __y = _M_node->_M_left;//向左边走,即令y指向左孩子
      while (__y->_M_right != )//y存在右孩子,
        __y = __y->_M_right;//一直往右走到底
      _M_node = __y;//最后即为解答
    }
    else {//即非根节点,且没有左孩子节点
      _Base_ptr __y = _M_node->_M_parent;//找出父节点
      while (_M_node == __y->_M_left) {//node节点是其父节点的左孩子
        _M_node = __y;//一直交替上溯
        __y = __y->_M_parent;//直到不为左孩子结点
      }
      _M_node = __y;//此时父节点即为解答
    }
  }
};

---

_Rb_tree_impl

template<typename _Key, typename _Val, typename _KeyOfValue,
typename _Compare, typename _Alloc = allocator<_Val> >
class _Rb_tree
{
//先说一下说这五个参数
/*
参数1 key key类型
参数2 val value和key的数据包
参数3 在数据包中取key得方法
参数4 key的排序方法
参数5 分配器
*/
...
protected:
    template<typename _Key_compare,
    bool _Is_pod_comparator = __is_pod(_Key_compare)>
    struct _Rb_tree_impl : public _Node_allocator
    {
      _Key_compare        _M_key_compare;
      _Rb_tree_node_base     _M_header;
      size_type         _M_node_count; // Keeps track of size of tree.

      _Rb_tree_impl()
      : _Node_allocator(), _M_key_compare(), _M_header(),
            _M_node_count()
      { _M_initialize(); }

      _Rb_tree_impl(const _Key_compare& __comp, const _Node_allocator& __a)
      : _Node_allocator(__a), _M_key_compare(__comp), _M_header(),
            _M_node_count()
      { _M_initialize(); }

#if __cplusplus >= 201103L
      _Rb_tree_impl(const _Key_compare& __comp, _Node_allocator&& __a)
      : _Node_allocator(std::move(__a)), _M_key_compare(__comp),
            _M_header(), _M_node_count()
      { _M_initialize(); }
#endif

        private:
      void
      _M_initialize()
      {
          this->_M_header._M_color = _S_red;
          this->_M_header._M_parent = ;
          this->_M_header._M_left = &this->_M_header;
          this->_M_header._M_right = &this->_M_header;
      }
        };

        _Rb_tree_impl<_Compare> _M_impl;
...
}

4.9的红黑树源码封装的比较严密,导致我没找到一些函数的实现,那么下面的源码分析,我就以我的学习笔记代替了

// 以下都是全域函式：__rb_tree_rotate_left(), __rb_tree_rotate_right(),
// __rb_tree_rebalance(), __rb_tree_rebalance_for_erase()  

//新节点必须为红色节点。如果安插处的父节点为红色，就违反了红黑色规则
//此时要旋转和改变颜色 

//左旋转
//节点x为左旋转点
inline void
_Rb_tree_rotate_left(_Rb_tree_node_base* __x, _Rb_tree_node_base*& __root)
{
  _Rb_tree_node_base* __y = __x->_M_right;//获取左旋转节点x的右孩子y
  __x->_M_right = __y->_M_left;//把y节点的左孩子作为旋转节点x的右孩子
  if (__y->_M_left !=)
    __y->_M_left->_M_parent = __x;//更新节点y左孩子父节点指针，指向新的父节点x
  __y->_M_parent = __x->_M_parent;//y节点替换x节点的位置

  //令y完全顶替x的地位（必须将x对其父节点的关系完全接收过来）
  if (__x == __root)//若原始位置节点x是根节点
    __root = __y;//则y为新的根节点
  //否则，若x节点是其父节点的左孩子
  else if (__x == __x->_M_parent->_M_left)
    __x->_M_parent->_M_left = __y;//则更新节点y为原始x父节点的左孩子
  else//若x节点是其父节点的右孩子
    __x->_M_parent->_M_right = __y;//则更新节点y为原始x父节点的右孩子
  __y->_M_left = __x;//旋转后旋转节点x作为节点y的左孩子
  __x->_M_parent = __y;//更新x节点的父节点指针
}

//右旋转
//节点x为右旋转点
inline void
_Rb_tree_rotate_right(_Rb_tree_node_base* __x, _Rb_tree_node_base*& __root)
{
  _Rb_tree_node_base* __y = __x->_M_left;//获取右旋转节点x的左孩子y
  __x->_M_left = __y->_M_right;//把y节点的右孩子作为旋转节点x的左孩子
  if (__y->_M_right != )
    __y->_M_right->_M_parent = __x;//更新节点y右孩子父节点指针，指向新的父节点x
  __y->_M_parent = __x->_M_parent;//y节点替换x节点的位置

  //令y完全顶替x的地位（必须将x对其父节点的关系完全接收过来）
  if (__x == __root)//若原始位置节点x是根节点
    __root = __y;//则y为新的根节点
  //否则，若x节点是其父节点的右孩子
  else if (__x == __x->_M_parent->_M_right)
    __x->_M_parent->_M_right = __y;//则更新节点y为原始x父节点的右孩子
  else//若x节点是其父节点的左孩子
    __x->_M_parent->_M_left = __y;//则更新节点y为原始x父节点的左孩子
  __y->_M_right = __x;//旋转后旋转节点x作为节点y的右孩子
  __x->_M_parent = __y;//更新x节点的父节点指针
}

//重新令RB-tree平衡（改变颜色和旋转）
//参数一为新增节点x，参数二为root节点
inline void
_Rb_tree_rebalance(_Rb_tree_node_base* __x, _Rb_tree_node_base*& __root)
{
  __x->_M_color = _S_rb_tree_red;//新插入的节点必须为红色,这样不会违反性质5.
  //若新插入节点不是为RB-Tree的根节点，且其父节点color属性也是红色,即违反了性质4.
  //则进入while循环.
  //此时根据节点x的父节点x->parent是其祖父节点x->parent->parent的左孩子还是右孩子进行讨论,
  //但是左右孩子之间是对称的，所以思想是类似的.
  while (__x != __root && __x->_M_parent->_M_color == _S_rb_tree_red) {
    //case1：节点x的父节点x->parent是其祖父节点x->parent->parent的左孩子
    if (__x->_M_parent == __x->_M_parent->_M_parent->_M_left) {
        //节点y为x节点的叔叔节点,即是节点x父节点x->parent的兄弟
      _Rb_tree_node_base* __y = __x->_M_parent->_M_parent->_M_right;
      if (__y && __y->_M_color == _S_rb_tree_red) {//情况1：若其叔叔节点y存在,且为红色
          /*
          此时x->parent和y都是红色的，解决办法是将x的父节点x->parent和叔叔结点y都着为黑色，
          而将x的祖父结点x->parent->parent着为红色，
          然后从祖父结点x->parent->parent继续向上判断是否破坏红黑树的性质。
          */
        __x->_M_parent->_M_color = _S_rb_tree_black;//将其父节点x->parent改变成黑色
        __y->_M_color = _S_rb_tree_black;//将其叔叔节点y改变成黑色
        __x->_M_parent->_M_parent->_M_color = _S_rb_tree_red;//将其祖父节点变成红色
        //把祖父节点作为当前节点,一直上溯,继续判断是否破坏RB-Tree性质.
        __x = __x->_M_parent->_M_parent;
      }
      else {//若无叔叔节点或者其叔叔节点y为黑色
          /*
          情况2：x的叔叔节点y是黑色且x是一个右孩子
          情况3：x的叔叔节点y是黑色且x是一个左孩子

         情况2和情况3中y都是黑色的，通过x是parent[x]的左孩子还是右孩子进行区分的。
         情况2中x是右孩子，可以在parent[x]结点将情况2通过左旋转为情况3，使得x变为左孩子。
         无论是间接还是直接的通过情况2进入到情况3，x的叔叔y总是黑色的。
         在情况3中，将parent[x]着为黑色，parent[parent[x]]着为红色，然后从parent[parent[x]]处进行一次右旋转。
         情况2、3修正了对性质4的违反，修正过程不会导致其他的红黑性质被破坏。
          */
        if (__x == __x->_M_parent->_M_right) {//若节点x为其父节点x->parent的右孩子
            //则以其父节点作为旋转节点
            //进行一次左旋转
          __x = __x->_M_parent;
          _Rb_tree_rotate_left(__x, __root);
          //旋转之后,节点x变成其父节点的左孩子
        }
        __x->_M_parent->_M_color = _S_rb_tree_black;//改变其父节点x->parent颜色
        __x->_M_parent->_M_parent->_M_color = _S_rb_tree_red;//改变其祖父节点x->parent->parent颜色
        _Rb_tree_rotate_right(__x->_M_parent->_M_parent, __root);//对其祖父节点进行一次右旋转
      }
    }
    //case2：节点x的父节点x->parent是其祖父节点x->parent->parent的右孩子
    //这种情况是跟上面的情况(父节点为其祖父节点的左孩子)是对称的.
    else {
        //节点y为x节点的叔叔节点,即是节点x父节点x->parent的兄弟
      _Rb_tree_node_base* __y = __x->_M_parent->_M_parent->_M_left;
      if (__y && __y->_M_color == _S_rb_tree_red) {//若叔叔节点存在,且为红色
        __x->_M_parent->_M_color = _S_rb_tree_black;//改变父节点颜色
        __y->_M_color = _S_rb_tree_black;//改变叔叔节点颜色
        __x->_M_parent->_M_parent->_M_color = _S_rb_tree_red;//改变祖父节点颜色
        __x = __x->_M_parent->_M_parent;//上溯祖父节点,判断是否违背RB-Tree的性质
      }
      else {//若叔叔节点不存在或叔叔节点为黑色
        if (__x == __x->_M_parent->_M_left) {//新节点x为其父节点的左孩子
            //对其父节点进行一次右旋转
          __x = __x->_M_parent;
          _Rb_tree_rotate_right(__x, __root);
        }
        __x->_M_parent->_M_color = _S_rb_tree_black;//改变父节点颜色
        __x->_M_parent->_M_parent->_M_color = _S_rb_tree_red;//改变祖父节点颜色
        _Rb_tree_rotate_left(__x->_M_parent->_M_parent, __root);//进行一次左旋转
      }
    }
  }
  //若新插入节点为根节点,则违反性质2
  //只需将其重新赋值为黑色即可
  __root->_M_color = _S_rb_tree_black;
}

//删除节点
inline _Rb_tree_node_base*
_Rb_tree_rebalance_for_erase(_Rb_tree_node_base* __z,
                             _Rb_tree_node_base*& __root,
                             _Rb_tree_node_base*& __leftmost,
                             _Rb_tree_node_base*& __rightmost)
{
  _Rb_tree_node_base* __y = __z;
  _Rb_tree_node_base* __x = ;
  _Rb_tree_node_base* __x_parent = ;
  if (__y->_M_left == )     // __z has at most one non-null child. y == z.
    __x = __y->_M_right;     // __x might be null.
  else
    if (__y->_M_right == )  // __z has exactly one non-null child. y == z.
      __x = __y->_M_left;    // __x is not null.
    else {                   // __z has two non-null children.  Set __y to
      __y = __y->_M_right;   //   __z's successor.  __x might be null.
      while (__y->_M_left != )
        __y = __y->_M_left;
      __x = __y->_M_right;
    }
  if (__y != __z) {          // relink y in place of z.  y is z's successor
    __z->_M_left->_M_parent = __y;
    __y->_M_left = __z->_M_left;
    if (__y != __z->_M_right) {
      __x_parent = __y->_M_parent;
      if (__x) __x->_M_parent = __y->_M_parent;
      __y->_M_parent->_M_left = __x;      // __y must be a child of _M_left
      __y->_M_right = __z->_M_right;
      __z->_M_right->_M_parent = __y;
    }
    else
      __x_parent = __y;
    if (__root == __z)
      __root = __y;
    else if (__z->_M_parent->_M_left == __z)
      __z->_M_parent->_M_left = __y;
    else
      __z->_M_parent->_M_right = __y;
    __y->_M_parent = __z->_M_parent;
    __STD::swap(__y->_M_color, __z->_M_color);
    __y = __z;
    // __y now points to node to be actually deleted
  }
  else {                        // __y == __z
    __x_parent = __y->_M_parent;
    if (__x) __x->_M_parent = __y->_M_parent;
    if (__root == __z)
      __root = __x;
    else
      if (__z->_M_parent->_M_left == __z)
        __z->_M_parent->_M_left = __x;
      else
        __z->_M_parent->_M_right = __x;
    if (__leftmost == __z)
      if (__z->_M_right == )        // __z->_M_left must be null also
        __leftmost = __z->_M_parent;
    // makes __leftmost == _M_header if __z == __root
      else
        __leftmost = _Rb_tree_node_base::_S_minimum(__x);
    if (__rightmost == __z)
      if (__z->_M_left == )         // __z->_M_right must be null also
        __rightmost = __z->_M_parent;
    // makes __rightmost == _M_header if __z == __root
      else                      // __x == __z->_M_left
        __rightmost = _Rb_tree_node_base::_S_maximum(__x);
  }
  if (__y->_M_color != _S_rb_tree_red) {
    while (__x != __root && (__x ==  || __x->_M_color == _S_rb_tree_black))
      if (__x == __x_parent->_M_left) {
        _Rb_tree_node_base* __w = __x_parent->_M_right;
        if (__w->_M_color == _S_rb_tree_red) {
          __w->_M_color = _S_rb_tree_black;
          __x_parent->_M_color = _S_rb_tree_red;
          _Rb_tree_rotate_left(__x_parent, __root);
          __w = __x_parent->_M_right;
        }
        if ((__w->_M_left ==  ||
             __w->_M_left->_M_color == _S_rb_tree_black) &&
            (__w->_M_right ==  ||
             __w->_M_right->_M_color == _S_rb_tree_black)) {
          __w->_M_color = _S_rb_tree_red;
          __x = __x_parent;
          __x_parent = __x_parent->_M_parent;
        } else {
          if (__w->_M_right ==  ||
              __w->_M_right->_M_color == _S_rb_tree_black) {
            if (__w->_M_left) __w->_M_left->_M_color = _S_rb_tree_black;
            __w->_M_color = _S_rb_tree_red;
            _Rb_tree_rotate_right(__w, __root);
            __w = __x_parent->_M_right;
          }
          __w->_M_color = __x_parent->_M_color;
          __x_parent->_M_color = _S_rb_tree_black;
          if (__w->_M_right) __w->_M_right->_M_color = _S_rb_tree_black;
          _Rb_tree_rotate_left(__x_parent, __root);
          break;
        }
      } else {                  // same as above, with _M_right <-> _M_left.
        _Rb_tree_node_base* __w = __x_parent->_M_left;
        if (__w->_M_color == _S_rb_tree_red) {
          __w->_M_color = _S_rb_tree_black;
          __x_parent->_M_color = _S_rb_tree_red;
          _Rb_tree_rotate_right(__x_parent, __root);
          __w = __x_parent->_M_left;
        }
        if ((__w->_M_right ==  ||
             __w->_M_right->_M_color == _S_rb_tree_black) &&
            (__w->_M_left ==  ||
             __w->_M_left->_M_color == _S_rb_tree_black)) {
          __w->_M_color = _S_rb_tree_red;
          __x = __x_parent;
          __x_parent = __x_parent->_M_parent;
        } else {
          if (__w->_M_left ==  ||
              __w->_M_left->_M_color == _S_rb_tree_black) {
            if (__w->_M_right) __w->_M_right->_M_color = _S_rb_tree_black;
            __w->_M_color = _S_rb_tree_red;
            _Rb_tree_rotate_left(__w, __root);
            __w = __x_parent->_M_left;
          }
          __w->_M_color = __x_parent->_M_color;
          __x_parent->_M_color = _S_rb_tree_black;
          if (__w->_M_left) __w->_M_left->_M_color = _S_rb_tree_black;
          _Rb_tree_rotate_right(__x_parent, __root);
          break;
        }
      }
    if (__x) __x->_M_color = _S_rb_tree_black;
  }
  return __y;
}

// Base class to encapsulate the differences between old SGI-style
// allocators and standard-conforming allocators.  In order to avoid
// having an empty base class, we arbitrarily move one of rb_tree's
// data members into the base class.

//以下是对内存分配的管理
#ifdef __STL_USE_STD_ALLOCATORS

// _Base for general standard-conforming allocators.
template <class _Tp, class _Alloc, bool _S_instanceless>
class _Rb_tree_alloc_base {
public:
  typedef typename _Alloc_traits<_Tp, _Alloc>::allocator_type allocator_type;
  allocator_type get_allocator() const { return _M_node_allocator; }//空间配置器的类型

  _Rb_tree_alloc_base(const allocator_type& __a)
    : _M_node_allocator(__a), _M_header() {}

protected:
  typename _Alloc_traits<_Rb_tree_node<_Tp>, _Alloc>::allocator_type
           _M_node_allocator;
  _Rb_tree_node<_Tp>* _M_header;//定义头指针，指向Rb_tree的根节点

  _Rb_tree_node<_Tp>* _M_get_node() //分配一个节点空间
    { return _M_node_allocator.allocate(); }
  void _M_put_node(_Rb_tree_node<_Tp>* __p) //释放一个节点空间
    { _M_node_allocator.deallocate(__p, ); }
};

// Specialization for instanceless allocators.
template <class _Tp, class _Alloc>
class _Rb_tree_alloc_base<_Tp, _Alloc, true> {
public:
  typedef typename _Alloc_traits<_Tp, _Alloc>::allocator_type allocator_type;
  allocator_type get_allocator() const { return allocator_type(); }

  _Rb_tree_alloc_base(const allocator_type&) : _M_header() {}

protected:
  _Rb_tree_node<_Tp>* _M_header;

  typedef typename _Alloc_traits<_Rb_tree_node<_Tp>, _Alloc>::_Alloc_type
          _Alloc_type;

  _Rb_tree_node<_Tp>* _M_get_node()
    { return _Alloc_type::allocate(); }
  void _M_put_node(_Rb_tree_node<_Tp>* __p)
    { _Alloc_type::deallocate(__p, ); }
};

//RB-Tree基本结构,即基类,继承_Rb_tree_alloc_base
template <class _Tp, class _Alloc>
struct _Rb_tree_base
  : public _Rb_tree_alloc_base<_Tp, _Alloc,
                               _Alloc_traits<_Tp, _Alloc>::_S_instanceless>
{
  typedef _Rb_tree_alloc_base<_Tp, _Alloc,
                              _Alloc_traits<_Tp, _Alloc>::_S_instanceless>
          _Base;
  typedef typename _Base::allocator_type allocator_type;

  _Rb_tree_base(const allocator_type& __a)
    : _Base(__a) { _M_header = _M_get_node(); }
  ~_Rb_tree_base() { _M_put_node(_M_header); }

};

#else /* __STL_USE_STD_ALLOCATORS */

//RB-Tree基本结构,即基类,没有继承_Rb_tree_alloc_base
template <class _Tp, class _Alloc>
struct _Rb_tree_base
{
  typedef _Alloc allocator_type;
  allocator_type get_allocator() const { return allocator_type(); }

  _Rb_tree_base(const allocator_type&)
    : _M_header() { _M_header = _M_get_node(); }
  ~_Rb_tree_base() { _M_put_node(_M_header); }

protected:
  _Rb_tree_node<_Tp>* _M_header;//定义头指针节点，指向根节点

  typedef simple_alloc<_Rb_tree_node<_Tp>, _Alloc> _Alloc_type;

  _Rb_tree_node<_Tp>* _M_get_node()
    { return _Alloc_type::allocate(); }
  void _M_put_node(_Rb_tree_node<_Tp>* __p)
    { _Alloc_type::deallocate(__p, ); }
};

#endif /* __STL_USE_STD_ALLOCATORS */

//RB-Tree类的定义,继承基类_Rb_tree_base
template <class _Key, class _Value, class _KeyOfValue, class _Compare,
          class _Alloc = __STL_DEFAULT_ALLOCATOR(_Value) >
class _Rb_tree : protected _Rb_tree_base<_Value, _Alloc> {
  typedef _Rb_tree_base<_Value, _Alloc> _Base;
protected:
  typedef _Rb_tree_node_base* _Base_ptr;
  typedef _Rb_tree_node<_Value> _Rb_tree_node;
  typedef _Rb_tree_Color_type _Color_type;
public:
  typedef _Key key_type;
  typedef _Value value_type;
  typedef value_type* pointer;
  typedef const value_type* const_pointer;
  typedef value_type& reference;
  typedef const value_type& const_reference;
  typedef _Rb_tree_node* _Link_type;
  typedef size_t size_type;
  typedef ptrdiff_t difference_type;

  typedef typename _Base::allocator_type allocator_type;
  allocator_type get_allocator() const { return _Base::get_allocator(); }

protected:
#ifdef __STL_USE_NAMESPACES
  using _Base::_M_get_node;
  using _Base::_M_put_node;
  using _Base::_M_header;//这里是指向根节点的节点指针
#endif /* __STL_USE_NAMESPACES */

protected:

//创建节点并对其初始化为x
_Link_type _M_create_node(const value_type& __x)
  {
    _Link_type __tmp = _M_get_node();//分配一个节点空间
    __STL_TRY {
      construct(&__tmp->_M_value_field, __x);//构造对象
    }
    __STL_UNWIND(_M_put_node(__tmp));
    return __tmp;
  }

//复制节点的值和颜色
  _Link_type _M_clone_node(_Link_type __x)
  {
    _Link_type __tmp = _M_create_node(__x->_M_value_field);
    __tmp->_M_color = __x->_M_color;
    __tmp->_M_left = ;
    __tmp->_M_right = ;
    return __tmp;
  }

  //释放节点
  void destroy_node(_Link_type __p)
  {
    destroy(&__p->_M_value_field);//析构对象
    _M_put_node(__p);//释放节点空间
  }

protected:
  size_type _M_node_count; // keeps track of size of tree
  _Compare _M_key_compare;    //节点键值比较准则

  //下面三个函数是用来获取header的成员
  _Link_type& _M_root() const
    { return (_Link_type&) _M_header->_M_parent; }
  _Link_type& _M_leftmost() const
    { return (_Link_type&) _M_header->_M_left; }
  _Link_type& _M_rightmost() const
    { return (_Link_type&) _M_header->_M_right; }

  //下面六个函数获取节点x的成员
  static _Link_type& _S_left(_Link_type __x)
    { return (_Link_type&)(__x->_M_left); }
  static _Link_type& _S_right(_Link_type __x)
    { return (_Link_type&)(__x->_M_right); }
  static _Link_type& _S_parent(_Link_type __x)
    { return (_Link_type&)(__x->_M_parent); }
  static reference _S_value(_Link_type __x)
    { return __x->_M_value_field; }
  static const _Key& _S_key(_Link_type __x)
    { return _KeyOfValue()(_S_value(__x)); }
  static _Color_type& _S_color(_Link_type __x)
    { return (_Color_type&)(__x->_M_color); }

  //跟上面六个函数功能相同，不同的是参数类型不同，一个是基类指针，一个是派生类指针
  static _Link_type& _S_left(_Base_ptr __x)
    { return (_Link_type&)(__x->_M_left); }
  static _Link_type& _S_right(_Base_ptr __x)
    { return (_Link_type&)(__x->_M_right); }
  static _Link_type& _S_parent(_Base_ptr __x)
    { return (_Link_type&)(__x->_M_parent); }
  static reference _S_value(_Base_ptr __x)
    { return ((_Link_type)__x)->_M_value_field; }
  static const _Key& _S_key(_Base_ptr __x)
    { return _KeyOfValue()(_S_value(_Link_type(__x)));}
  static _Color_type& _S_color(_Base_ptr __x)
    { return (_Color_type&)(_Link_type(__x)->_M_color); }

  //RB-Tree的极小值
  static _Link_type _S_minimum(_Link_type __x)
    { return (_Link_type)  _Rb_tree_node_base::_S_minimum(__x); }

   //RB-Tree的极大值
  static _Link_type _S_maximum(_Link_type __x)
    { return (_Link_type) _Rb_tree_node_base::_S_maximum(__x); }

public:
    //迭代器
  typedef _Rb_tree_iterator<value_type, reference, pointer> iterator;
  typedef _Rb_tree_iterator<value_type, const_reference, const_pointer>
          const_iterator;

#ifdef __STL_CLASS_PARTIAL_SPECIALIZATION
  typedef reverse_iterator<const_iterator> const_reverse_iterator;
  typedef reverse_iterator<iterator> reverse_iterator;
#else /* __STL_CLASS_PARTIAL_SPECIALIZATION */
  typedef reverse_bidirectional_iterator<iterator, value_type, reference,
                                         difference_type>
          reverse_iterator;
  typedef reverse_bidirectional_iterator<const_iterator, value_type,
                                         const_reference, difference_type>
          const_reverse_iterator;
#endif /* __STL_CLASS_PARTIAL_SPECIALIZATION */ 

private:
    //类的私有成员函数,在后面定义
  iterator _M_insert(_Base_ptr __x, _Base_ptr __y, const value_type& __v);
  _Link_type _M_copy(_Link_type __x, _Link_type __p);
  void _M_erase(_Link_type __x);

public:
                                // allocation/deallocation
  _Rb_tree()
    : _Base(allocator_type()), _M_node_count(), _M_key_compare()
    { _M_empty_initialize(); }

  _Rb_tree(const _Compare& __comp)
    : _Base(allocator_type()), _M_node_count(), _M_key_compare(__comp)
    { _M_empty_initialize(); }

  _Rb_tree(const _Compare& __comp, const allocator_type& __a)
    : _Base(__a), _M_node_count(), _M_key_compare(__comp)
    { _M_empty_initialize(); }

  _Rb_tree(const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __x)
    : _Base(__x.get_allocator()),
      _M_node_count(), _M_key_compare(__x._M_key_compare)
  {
    if (__x._M_root() == )
      _M_empty_initialize();
    else {
      _S_color(_M_header) = _S_rb_tree_red;
      _M_root() = _M_copy(__x._M_root(), _M_header);
      _M_leftmost() = _S_minimum(_M_root());
      _M_rightmost() = _S_maximum(_M_root());
    }
    _M_node_count = __x._M_node_count;
  }
  ~_Rb_tree() { clear(); }
  _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>&
  operator=(const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __x);

private:
    //初始化header
  void _M_empty_initialize() {
    _S_color(_M_header) = _S_rb_tree_red; // used to distinguish header from
                                          // __root, in iterator.operator++
    _M_root() = ;
    _M_leftmost() = _M_header;
    _M_rightmost() = _M_header;
  }

public:
                                // accessors:
  _Compare key_comp() const { return _M_key_compare; }
  iterator begin() { return _M_leftmost(); }//RB-Tree的起始迭代器为最小节点
  const_iterator begin() const { return _M_leftmost(); }
  iterator end() { return _M_header; }//RB-Tree的结束迭代器为header
  const_iterator end() const { return _M_header; }
  reverse_iterator rbegin() { return reverse_iterator(end()); }
  const_reverse_iterator rbegin() const {
    return const_reverse_iterator(end());
  }
  reverse_iterator rend() { return reverse_iterator(begin()); }
  const_reverse_iterator rend() const {
    return const_reverse_iterator(begin());
  }
  //RB-Tree是否为空
  bool empty() const { return _M_node_count == ; }
  //RB-Tree节点数
  size_type size() const { return _M_node_count; }
  size_type max_size() const { return size_type(-); }

  //交换两棵RB-Tree的内容
  //RB-tree只有三个表现成员，所以两棵RB-Tree交换内容时，只需互换这3个成员
  void swap(_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __t) {
    __STD::swap(_M_header, __t._M_header);
    __STD::swap(_M_node_count, __t._M_node_count);
    __STD::swap(_M_key_compare, __t._M_key_compare);
  }

public:
                                // insert/erase
    //插入节点,但是节点值必须唯一
  pair<iterator,bool> insert_unique(const value_type& __x);
  //插入节点,节点值可以与当前RB-Tree节点值相等
  iterator insert_equal(const value_type& __x);

  //在指定位置插入节点
  iterator insert_unique(iterator __position, const value_type& __x);
  iterator insert_equal(iterator __position, const value_type& __x);

#ifdef __STL_MEMBER_TEMPLATES
  template <class _InputIterator>
  void insert_unique(_InputIterator __first, _InputIterator __last);
  template <class _InputIterator>
  void insert_equal(_InputIterator __first, _InputIterator __last);
#else /* __STL_MEMBER_TEMPLATES */
  void insert_unique(const_iterator __first, const_iterator __last);
  void insert_unique(const value_type* __first, const value_type* __last);
  void insert_equal(const_iterator __first, const_iterator __last);
  void insert_equal(const value_type* __first, const value_type* __last);
#endif /* __STL_MEMBER_TEMPLATES */

  //删除节点
  void erase(iterator __position);
  size_type erase(const key_type& __x);
  void erase(iterator __first, iterator __last);
  void erase(const key_type* __first, const key_type* __last);
  //清除RB-Tree
  void clear() {
    if (_M_node_count != ) {
      _M_erase(_M_root());
      _M_leftmost() = _M_header;
      _M_root() = ;
      _M_rightmost() = _M_header;
      _M_node_count = ;
    }
  }      

public:
                                // set operations:
  iterator find(const key_type& __x);
  const_iterator find(const key_type& __x) const;
  size_type count(const key_type& __x) const;
  iterator lower_bound(const key_type& __x);
  const_iterator lower_bound(const key_type& __x) const;
  iterator upper_bound(const key_type& __x);
  const_iterator upper_bound(const key_type& __x) const;
  pair<iterator,iterator> equal_range(const key_type& __x);
  pair<const_iterator, const_iterator> equal_range(const key_type& __x) const;

public:
                                // Debugging.
  bool __rb_verify() const;
};

//以下是操作符重载
//重载operator==运算符，使用的是STL泛型算法
template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
inline bool
operator==(const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __x,
           const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __y)
{
  return __x.size() == __y.size() &&
      //STL的算法equal(__x.begin(), __x.end(), __y.begin());
         equal(__x.begin(), __x.end(), __y.begin());
}
 //重载operator<运算符，使用的是STL泛型算法
template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
inline bool
operator<(const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __x,
          const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __y)
{
  return lexicographical_compare(__x.begin(), __x.end(),
                                 __y.begin(), __y.end());
}

#ifdef __STL_FUNCTION_TMPL_PARTIAL_ORDER

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
inline bool
operator!=(const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __x,
           const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __y) {
  return !(__x == __y);
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
inline bool
operator>(const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __x,
          const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __y) {
  return __y < __x;
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
inline bool
operator<=(const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __x,
           const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __y) {
  return !(__y < __x);
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
inline bool
operator>=(const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __x,
           const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __y) {
  return !(__x < __y);
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
inline void
swap(_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __x,
     _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __y)
{
  __x.swap(__y);
}

#endif /* __STL_FUNCTION_TMPL_PARTIAL_ORDER */

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>&
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::operator=(const _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>& __x)
{
  if (this != &__x) {
                                // Note that _Key may be a constant type.
    clear();
    _M_node_count = ;
    _M_key_compare = __x._M_key_compare;
    if (__x._M_root() == ) {
      _M_root() = ;
      _M_leftmost() = _M_header;
      _M_rightmost() = _M_header;
    }
    else {
      _M_root() = _M_copy(__x._M_root(), _M_header);
      _M_leftmost() = _S_minimum(_M_root());
      _M_rightmost() = _S_maximum(_M_root());
      _M_node_count = __x._M_node_count;
    }
  }
  return *this;
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::_M_insert(_Base_ptr __x_, _Base_ptr __y_, const _Value& __v)
{//参数x_为新值插入点，参数y_为插入点之父节点，参数v 为新值
  _Link_type __x = (_Link_type) __x_;
  _Link_type __y = (_Link_type) __y_;
  _Link_type __z;

  if (__y == _M_header || __x !=  ||
      _M_key_compare(_KeyOfValue()(__v), _S_key(__y))) {
    __z = _M_create_node(__v);//创建值为v的节点z
    _S_left(__y) = __z;               // also makes _M_leftmost() = __z
                                      //    when __y == _M_header
    if (__y == _M_header) {
      _M_root() = __z;
      _M_rightmost() = __z;
    }
    else if (__y == _M_leftmost())//若y为最左节点
      _M_leftmost() = __z;   // maintain _M_leftmost() pointing to min node
  }
  else {
    __z = _M_create_node(__v);
    _S_right(__y) = __z;
    if (__y == _M_rightmost())
      _M_rightmost() = __z;  // maintain _M_rightmost() pointing to max node
  }
  _S_parent(__z) = __y;//设定新节点的父节点
  _S_left(__z) = ;//设定新节点的左孩子
  _S_right(__z) = ;//设定新节点的右孩子
  _Rb_tree_rebalance(__z, _M_header->_M_parent);//调整RB-Tree使其满足性质
  ++_M_node_count;//节点数增加1
  return iterator(__z);//返回新节点迭代器
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::insert_equal(const _Value& __v)
{
  _Link_type __y = _M_header;
  _Link_type __x = _M_root();//从根节点开始
  while (__x != ) {//从根节点开始,往下寻找合适插入点
    __y = __x;
    //判断新插入节点值与当前节点x值的大小,以便判断往x的左边走还是往右边走
    __x = _M_key_compare(_KeyOfValue()(__v), _S_key(__x)) ?
            _S_left(__x) : _S_right(__x);
  }
  return _M_insert(__x, __y, __v);
}

// 安插新值；节点键值不允许重复，若重复则安插无效。
// 注意，传回值是个pair，第一元素是个 RB-tree 迭代器，指向新增节点，
// 第二元素表示安插成功与否。
template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
pair<typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator,
     bool>
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::insert_unique(const _Value& __v)
{
  _Link_type __y = _M_header;
  _Link_type __x = _M_root();//从根节点开始
  bool __comp = true;
  while (__x != ) {//从根节点开始,往下寻找合适插入点
    __y = __x;
    //判断新插入节点值与当前节点x值的大小,以便判断往x的左边走还是往右边走
    __comp = _M_key_compare(_KeyOfValue()(__v), _S_key(__x));
    __x = __comp ? _S_left(__x) : _S_right(__x);
  }
  //离开while循环之后，y所指即为安插点的父节点，x必为叶子节点
  iterator __j = iterator(__y);//令迭代器j指向插入节点之父节点y
  if (__comp)//若为真
    if (__j == begin())//若插入点之父节点为最左节点
      return pair<iterator,bool>(_M_insert(__x, __y, __v), true);
    else//否则(插入点之父节点不在最左节点)
      --__j;//调整j
   // 小于新值（表示遇「小」，将安插于右侧）
  if (_M_key_compare(_S_key(__j._M_node), _KeyOfValue()(__v)))
    return pair<iterator,bool>(_M_insert(__x, __y, __v), true);
  //若运行到这里，表示键值有重复，不应该插入
  return pair<iterator,bool>(__j, false);
}

template <class _Key, class _Val, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>::iterator
_Rb_tree<_Key, _Val, _KeyOfValue, _Compare, _Alloc>
  ::insert_unique(iterator __position, const _Val& __v)
{
  if (__position._M_node == _M_header->_M_left) { // begin()
    if (size() >  &&
        _M_key_compare(_KeyOfValue()(__v), _S_key(__position._M_node)))
      return _M_insert(__position._M_node, __position._M_node, __v);
    // first argument just needs to be non-null
    else
      return insert_unique(__v).first;
  } else if (__position._M_node == _M_header) { // end()
    if (_M_key_compare(_S_key(_M_rightmost()), _KeyOfValue()(__v)))
      return _M_insert(, _M_rightmost(), __v);
    else
      return insert_unique(__v).first;
  } else {
    iterator __before = __position;
    --__before;
    if (_M_key_compare(_S_key(__before._M_node), _KeyOfValue()(__v))
        && _M_key_compare(_KeyOfValue()(__v), _S_key(__position._M_node))) {
      if (_S_right(__before._M_node) == )
        return _M_insert(, __before._M_node, __v);
      else
        return _M_insert(__position._M_node, __position._M_node, __v);
    // first argument just needs to be non-null
    } else
      return insert_unique(__v).first;
  }
}

template <class _Key, class _Val, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Val,_KeyOfValue,_Compare,_Alloc>::iterator
_Rb_tree<_Key,_Val,_KeyOfValue,_Compare,_Alloc>
  ::insert_equal(iterator __position, const _Val& __v)
{
  if (__position._M_node == _M_header->_M_left) { // begin()
    if (size() >  &&
        !_M_key_compare(_S_key(__position._M_node), _KeyOfValue()(__v)))
      return _M_insert(__position._M_node, __position._M_node, __v);
    // first argument just needs to be non-null
    else
      return insert_equal(__v);
  } else if (__position._M_node == _M_header) {// end()
    if (!_M_key_compare(_KeyOfValue()(__v), _S_key(_M_rightmost())))
      return _M_insert(, _M_rightmost(), __v);
    else
      return insert_equal(__v);
  } else {
    iterator __before = __position;
    --__before;
    if (!_M_key_compare(_KeyOfValue()(__v), _S_key(__before._M_node))
        && !_M_key_compare(_S_key(__position._M_node), _KeyOfValue()(__v))) {
      if (_S_right(__before._M_node) == )
        return _M_insert(, __before._M_node, __v);
      else
        return _M_insert(__position._M_node, __position._M_node, __v);
    // first argument just needs to be non-null
    } else
      return insert_equal(__v);
  }
}

#ifdef __STL_MEMBER_TEMPLATES  

template <class _Key, class _Val, class _KoV, class _Cmp, class _Alloc>
  template<class _II>
void _Rb_tree<_Key,_Val,_KoV,_Cmp,_Alloc>
  ::insert_equal(_II __first, _II __last)
{
  for ( ; __first != __last; ++__first)
    insert_equal(*__first);
}

template <class _Key, class _Val, class _KoV, class _Cmp, class _Alloc>
  template<class _II>
void _Rb_tree<_Key,_Val,_KoV,_Cmp,_Alloc>
  ::insert_unique(_II __first, _II __last) {
  for ( ; __first != __last; ++__first)
    insert_unique(*__first);
}

#else /* __STL_MEMBER_TEMPLATES */

template <class _Key, class _Val, class _KoV, class _Cmp, class _Alloc>
void
_Rb_tree<_Key,_Val,_KoV,_Cmp,_Alloc>
  ::insert_equal(const _Val* __first, const _Val* __last)
{
  for ( ; __first != __last; ++__first)
    insert_equal(*__first);
}

template <class _Key, class _Val, class _KoV, class _Cmp, class _Alloc>
void
_Rb_tree<_Key,_Val,_KoV,_Cmp,_Alloc>
  ::insert_equal(const_iterator __first, const_iterator __last)
{
  for ( ; __first != __last; ++__first)
    insert_equal(*__first);
}

template <class _Key, class _Val, class _KoV, class _Cmp, class _Alloc>
void
_Rb_tree<_Key,_Val,_KoV,_Cmp,_Alloc>
  ::insert_unique(const _Val* __first, const _Val* __last)
{
  for ( ; __first != __last; ++__first)
    insert_unique(*__first);
}

template <class _Key, class _Val, class _KoV, class _Cmp, class _Alloc>
void _Rb_tree<_Key,_Val,_KoV,_Cmp,_Alloc>
  ::insert_unique(const_iterator __first, const_iterator __last)
{
  for ( ; __first != __last; ++__first)
    insert_unique(*__first);
}

#endif /* __STL_MEMBER_TEMPLATES */

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
inline void _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::erase(iterator __position)
{
  _Link_type __y =
    (_Link_type) _Rb_tree_rebalance_for_erase(__position._M_node,
                                              _M_header->_M_parent,
                                              _M_header->_M_left,
                                              _M_header->_M_right);
  destroy_node(__y);
  --_M_node_count;
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::size_type
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::erase(const _Key& __x)
{
  pair<iterator,iterator> __p = equal_range(__x);
  size_type __n = ;
  distance(__p.first, __p.second, __n);
  erase(__p.first, __p.second);
  return __n;
}

template <class _Key, class _Val, class _KoV, class _Compare, class _Alloc>
typename _Rb_tree<_Key, _Val, _KoV, _Compare, _Alloc>::_Link_type
_Rb_tree<_Key,_Val,_KoV,_Compare,_Alloc>
  ::_M_copy(_Link_type __x, _Link_type __p)
{
                        // structural copy.  __x and __p must be non-null.
  _Link_type __top = _M_clone_node(__x);
  __top->_M_parent = __p;

  __STL_TRY {
    if (__x->_M_right)
      __top->_M_right = _M_copy(_S_right(__x), __top);
    __p = __top;
    __x = _S_left(__x);

    while (__x != ) {
      _Link_type __y = _M_clone_node(__x);
      __p->_M_left = __y;
      __y->_M_parent = __p;
      if (__x->_M_right)
        __y->_M_right = _M_copy(_S_right(__x), __y);
      __p = __y;
      __x = _S_left(__x);
    }
  }
  __STL_UNWIND(_M_erase(__top));

  return __top;
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
void _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::_M_erase(_Link_type __x)
{
                                // erase without rebalancing
  while (__x != ) {
    _M_erase(_S_right(__x));
    _Link_type __y = _S_left(__x);
    destroy_node(__x);
    __x = __y;
  }
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
void _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::erase(iterator __first, iterator __last)
{
  if (__first == begin() && __last == end())
    clear();
  else
    while (__first != __last) erase(__first++);
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
void _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::erase(const _Key* __first, const _Key* __last)
{
  while (__first != __last) erase(*__first++);
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::find(const _Key& __k)
{
  _Link_type __y = _M_header;      // Last node which is not less than __k.
  _Link_type __x = _M_root();      // Current node. 

  while (__x != )
    if (!_M_key_compare(_S_key(__x), __k))
      __y = __x, __x = _S_left(__x);
    else
      __x = _S_right(__x);

  iterator __j = iterator(__y);
  return (__j == end() || _M_key_compare(__k, _S_key(__j._M_node))) ?
     end() : __j;
}

//查找RB树中是否有键值为k的节点
template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::const_iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::find(const _Key& __k) const
{
  _Link_type __y = _M_header; /* Last node which is not less than __k. */
  _Link_type __x = _M_root(); /* Current node. */

  while (__x != ) {
    if (!_M_key_compare(_S_key(__x), __k))//若k比当前节点x键值小
      __y = __x, __x = _S_left(__x);
    else
      __x = _S_right(__x);
  }
  const_iterator __j = const_iterator(__y);
  return (__j == end() || _M_key_compare(__k, _S_key(__j._M_node))) ?
    end() : __j;
}

//计算RB树中键值为k的节点的个数
template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::size_type
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::count(const _Key& __k) const
{
  pair<const_iterator, const_iterator> __p = equal_range(__k);
  size_type __n = ;
  distance(__p.first, __p.second, __n);
  return __n;
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::lower_bound(const _Key& __k)
{
  _Link_type __y = _M_header; /* Last node which is not less than __k. */
  _Link_type __x = _M_root(); /* Current node. */

  while (__x != )
    if (!_M_key_compare(_S_key(__x), __k))
      __y = __x, __x = _S_left(__x);
    else
      __x = _S_right(__x);

  return iterator(__y);
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::const_iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::lower_bound(const _Key& __k) const
{
  _Link_type __y = _M_header; /* Last node which is not less than __k. */
  _Link_type __x = _M_root(); /* Current node. */

  while (__x != )
    if (!_M_key_compare(_S_key(__x), __k))
      __y = __x, __x = _S_left(__x);
    else
      __x = _S_right(__x);

  return const_iterator(__y);
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::upper_bound(const _Key& __k)
{
  _Link_type __y = _M_header; /* Last node which is greater than __k. */
  _Link_type __x = _M_root(); /* Current node. */

   while (__x != )
     if (_M_key_compare(__k, _S_key(__x)))
       __y = __x, __x = _S_left(__x);
     else
       __x = _S_right(__x);

   return iterator(__y);
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::const_iterator
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::upper_bound(const _Key& __k) const
{
  _Link_type __y = _M_header; /* Last node which is greater than __k. */
  _Link_type __x = _M_root(); /* Current node. */

   while (__x != )
     if (_M_key_compare(__k, _S_key(__x)))
       __y = __x, __x = _S_left(__x);
     else
       __x = _S_right(__x);

   return const_iterator(__y);
}

template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
inline
pair<typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator,
     typename _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::iterator>
_Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>
  ::equal_range(const _Key& __k)
{
  return pair<iterator, iterator>(lower_bound(__k), upper_bound(__k));
}

template <class _Key, class _Value, class _KoV, class _Compare, class _Alloc>
inline
pair<typename _Rb_tree<_Key, _Value, _KoV, _Compare, _Alloc>::const_iterator,
     typename _Rb_tree<_Key, _Value, _KoV, _Compare, _Alloc>::const_iterator>
_Rb_tree<_Key, _Value, _KoV, _Compare, _Alloc>
  ::equal_range(const _Key& __k) const
{
  return pair<const_iterator,const_iterator>(lower_bound(__k),
                                             upper_bound(__k));
}

//计算从 node 至 root路径中的黑节点数量
inline int
__black_count(_Rb_tree_node_base* __node, _Rb_tree_node_base* __root)
{
  if (__node == )
    return ;
  else {
    int __bc = __node->_M_color == _S_rb_tree_black ?  : ;//若节点node为黑色,则bc为1
    if (__node == __root)//判断node是否为根节点
      return __bc;
    else
      return __bc + __black_count(__node->_M_parent, __root);//递归调用
  }
}

//验证己生这棵树是否符合RB树条件
template <class _Key, class _Value, class _KeyOfValue,
          class _Compare, class _Alloc>
bool _Rb_tree<_Key,_Value,_KeyOfValue,_Compare,_Alloc>::__rb_verify() const
{
    //空树
  if (_M_node_count ==  || begin() == end())
    return _M_node_count ==  && begin() == end() &&
      _M_header->_M_left == _M_header && _M_header->_M_right == _M_header;

  //最左节点到根节点的黑色节点数
  int __len = __black_count(_M_leftmost(), _M_root());
  //一下走访整个RB树，针对每个节点（从最小到最大）……
  for (const_iterator __it = begin(); __it != end(); ++__it) {
    _Link_type __x = (_Link_type) __it._M_node;
    _Link_type __L = _S_left(__x);
    _Link_type __R = _S_right(__x);

    if (__x->_M_color == _S_rb_tree_red)//违背性质4
        //如果一个节点是红色的，则它的两个孩子节点都是黑色的。
      if ((__L && __L->_M_color == _S_rb_tree_red) ||
          (__R && __R->_M_color == _S_rb_tree_red))
        return false;

    //以下是违背二叉查找树性质
    //节点的左孩子节点键值小于该节点键值
    //节点的右孩子节点键值大于该节点键值
    if (__L && _M_key_compare(_S_key(__x), _S_key(__L)))
      return false;
    if (__R && _M_key_compare(_S_key(__R), _S_key(__x)))
      return false;

    //[叶子结点到root]路径内的黑色节点数，与[最左节点至root]路径内的黑色节点不同。不符合RB树要求
    //违背性质5
    if (!__L && !__R && __black_count(__x, _M_root()) != __len)
      return false;
  }

  if (_M_leftmost() != _Rb_tree_node_base::_S_minimum(_M_root()))
    return false; // 最左节点不为最小节点，不符合二叉查找树的要求
  if (_M_rightmost() != _Rb_tree_node_base::_S_maximum(_M_root()))
    return false;// 最右节点不为最大节点，不符不符合二叉查找树的要求

  return true;
} 

参考<<侯捷STL源码剖析>>