codevs 1080 线段树点修改

先来介绍一下线段树。

线段树是一个把线段，或者说一个区间储存在二叉树中。如图所示的就是一棵线段树，它维护一个区间的和。

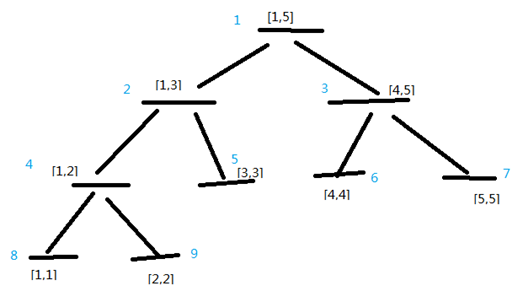
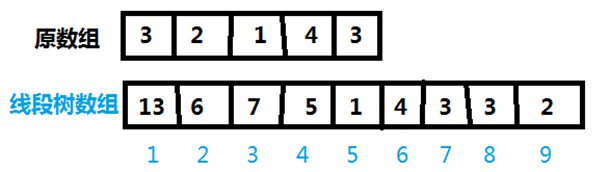
蓝色数字的是线段树的节点在数组中的位置，它表示的区间已经在图上标出，它的值就是这段区间的和。

比如说线段树1号节点表示[1,5]区间，它的值是13，也就是原数组1号位到5号位所有数字加起来的和。

不难发现线段树的下标有这样的性质：

1. 设一个节点的下号是o，那么它的左子树是o*2，右子树是o*2+1。

2. 线段树的大小是原数组的大小*2-1。

3. 线段树叶节点表示区间的长度为1，也就是一个数字，此时区间的左边界=区间的右边界。

但是我们实际使用的时候，线段树是用一个长度为原数组大小4倍的数组储存的，因为方便处理，防止访问叶节点时下标越界。

它支持几种操作：

1. 修改一个点的值

2. 将一个区间加上或减去某个数

3. 查询一个区间的和（乘积也可以），最大/最小值

4. 将一个区间值改变成某个大于0的数

以上时间复杂度都是logn。

建立线段树：

这里我采用递归的方式。在函数内设3个参数，这个线段树节点的下标o，它表示的左区间L，又区间R。从根节点开始递归，如果L=R，就是走到了叶节点（根据性质3），那么该点就是原数组第L（或R）位的值，否则分成两个区间，递归它的左右子树。

代码如下：

 void init(int o,int L,int R)
 {
     if(L==R) sumv[o]=A[L];  //A[]是原数组，sumv[]是线段树数组
     else
     {
         int M=(L+R)/;
         init(o*,L,M);
         init(o*+,M+,R);
         sumv[o]=sumv[o*]+sumv[o*+];
     }
 }

这里的sumv是求和线段树数组，我以这个为例。当然如果是维护区间最大/最小，那么第9行的代码应该是左右子树的最大/最小值。

调用：

init（1,1,n）;

// 1，n是总区间。

点修改：

与建树的过程类似，从根节点开始，一直递归到叶节点，然后直接修改，完成之后，更新sumv值就可以了。

如果把修改原数组p号位的值修改为v。

代码：

 int p,v;
 
 void update(int o,int L,int R)
 {
     if(L==R) sumv[o]=v;
     else
     {
         int M=(L+R)/;
         if(p<=M) update(o*,L,M); else update(o*+,M+,R);
         sumv[o]=sumv[o*]+sumv[o*+];
     }
 }

调用：

先把p，和v赋值好，然后直接调用即可

p=x,v=y;//x,y是你要赋的值

update(1,1,n);

查询区间的和：

还是与上面类似。从根节点开始递归。如果这一层的区间[L,R]包含于要求的区间[y1,y2]，那么就把这一层的值累加，否则就访问它的子树，把这个区间一份为二。

如果它的子树表示的区间与要求的区间有交集，就说明有需要访问，否则就不用。

代码：

 int y1,y2,ans;
 void query(int o,int L,int R)
 {
     if(y1<=L && R<=y2)     ans+=sumv[o];
     else
     {
         int M=(L+R)/;
         if(y1<=M) query(o*,L,M);
         if(y2>M) query(o*+,M+,R);
     }
 }

调用：

把要查找的区间y1,y2赋值好，并把存储答案的ans清0，,再调用即可

y1=x,y2=y,ans=0;//注意ans一定要初始化，最后查出来的答案是保存在ans里面的。

query(1,1,n);

点修改的说明就到此。

测试的题目：codevs 1080 线段树练习

链接：http://codevs.cn/problem/1080/

附代码：

 #include<cstdio>
 #include<iostream>
 using namespace std;
 const int maxn=;
 
 int A[maxn],sumv[maxn*],n,m;
 
 void init(int o,int L,int R)
 {
     if(L==R) sumv[o]=A[L];
     else
     {
         int M=(L+R)/;
         init(o*,L,M);
         init(o*+,M+,R);
         sumv[o]=sumv[o*]+sumv[o*+];
     }
 }
 
 int p,v;
 void update(int o,int L,int R)
 {
     if(L==R) sumv[o]=v;
     else
     {
         int M=(L+R)/;
         if(p<=M) update(o*,L,M); else update(o*+,M+,R);
         sumv[o]=sumv[o*]+sumv[o*+];
     }
 }
 
 int y1,y2,ans;
 void query(int o,int L,int R)
 {
     if(y1<=L && R<=y2)     ans+=sumv[o];
     else
     {
         int M=(L+R)/;
         if(y1<=M) query(o*,L,M);
         if(y2>M) query(o*+,M+,R);
     }
 }
 
 int main()
 {
     cin>>n;
     for(int i=;i<=n;i++) cin>>A[i];
     init(,,n);
     cin>>m;
     for(int i=,k,x,y;i<=m;i++)
     {
         cin>>k>>x>>y;
         if(k==)
         {
             p=x,v=A[p]+y;
             A[p]=v;
             update(,,n);
         }
         else
         {
             y1=x,y2=y,ans=;
             query(,,n);
             cout<<ans<<endl;
         }
     }
     return ;
 }