【NOIP2015提高组】 Day2 T3 运输计划

题目描述

L 国有 n 个星球,还有 n-1 条双向航道,每条航道建立在两个星球之间,这 n-1 条航道连通了 L 国的所有星球。

小 P 掌管一家物流公司,该公司有很多个运输计划,每个运输计划形如:有一艘物

流飞船需要从 ui 号星球沿最快的宇航路径飞行到 vi 号星球去。显然,飞船驶过一条航道是需要时间的,对于航道 j,任意飞船驶过它所花费的时间为 tj,并且任意两艘飞船之间不会产生任何干扰。

为了鼓励科技创新,L 国国王同意小 P 的物流公司参与 L 国的航道建设,即允许小 P 把某一条航道改造成虫洞,飞船驶过虫洞不消耗时间。

在虫洞的建设完成前小 P 的物流公司就预接了 m 个运输计划。在虫洞建设完成后, 这 m 个运输计划会同时开始,所有飞船一起出发。当这 m 个运输计划都完成时,小 P 的物流公司的阶段性工作就完成了。

如果小 P 可以自由选择将哪一条航道改造成虫洞,试求出小 P 的物流公司完成阶段性工作所需要的最短时间是多少?

输入输出格式

输入格式：

输入文件名为 transport.in。

第一行包括两个正整数 n、m,表示 L 国中星球的数量及小 P 公司预接的运输计划的数量,星球从 1 到 n 编号。

接下来 n-1 行描述航道的建设情况,其中第 i 行包含三个整数 ai, bi 和 ti,表示第

i 条双向航道修建在 ai 与 bi 两个星球之间,任意飞船驶过它所花费的时间为 ti。

接下来 m 行描述运输计划的情况,其中第 j 行包含两个正整数 uj 和 vj,表示第 j个运输计划是从 uj 号星球飞往 vj 号星球。

输出格式：

输出共1行,包含1个整数,表示小P的物流公司完成阶段性工作所需要的最短时间。

输入输出样例

输入样例#1：

输出样例#1：

说明

所有测试数据的范围和特点如下表所示

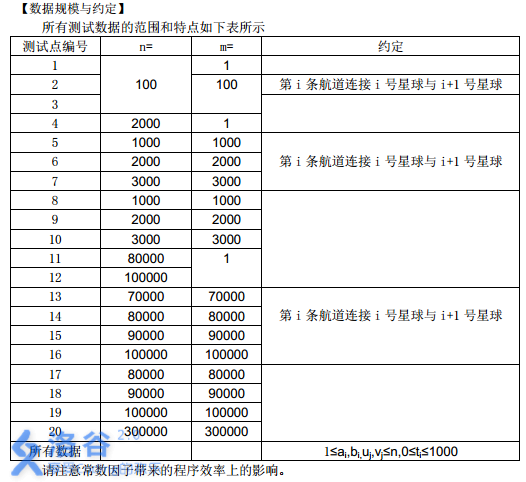
请注意常数因子带来的程序效率上的影响。

自测考场上因为时间被T1卡了时间，结果代码出了偏差，只剩下5分.....

首先，先用倍增处理出每个任务的耗时，将所有的任务按耗时排序。然后二分，假设删除一条边后所有任务中最大耗时≤mid，随后在不删除任何边的条件下找出这n个任务中耗时＞mid的所有任务，若要使这些任务的耗时降低至mid同时使最终答案尽可能地小，则所删除的那条边必满足其同时在这些任务的路径中且最长。若不存在符合条件的边或(最长耗时-符合条件最长边长度)>mid 则l=mid+1,否则r=mid，最终输出l即可。

 #pragma comment(linker, "/STACK:102400000,102400000")

 #include<iostream>

 #include<cstdio>

 #include<cstring>

 #include<algorithm>

 #define M 310000

 using namespace std;

 struct edge{int u,v,next;}e[M*]={}; int use=,head[M]={};

 void add(int x,int y,int z){use++;e[use].u=y; e[use].v=z; e[use].next=head[x]; head[x]=use;}

 int dep[M]={},dis[M][]={},f[M][]={};

 void dfs(int x,int fa,int v){

     dep[x]=dep[fa]+; dis[x][]=v; f[x][]=fa;

     for(int i=;i<;i++) f[x][i]=f[f[x][i-]][i-],dis[x][i]=dis[x][i-]+dis[f[x][i-]][i-];

     for(int i=head[x];i;i=e[i].next) if(e[i].u!=fa) dfs(e[i].u,x,e[i].v);

 }

 int getlca(int x,int y){

     if(dep[x]<dep[y]) swap(x,y); int cha=(dep[x]-dep[y]);

     for(int i=;i>=;i--) if((<<i)&cha) x=f[x][i];

     for(int i=;i>=;i--) if(f[x][i]!=f[y][i]) x=f[x][i],y=f[y][i];

     if(x!=y) return f[x][]; return x;

 }

 int getdis(int x,int y){

     int lca=getlca(x,y),ans=;

     int cha=dep[x]-dep[lca];

     for(int i=;i>=;i--) if((<<i)&cha) ans+=dis[x][i],x=f[x][i];

     cha=dep[y]-dep[lca];

     for(int i=;i>=;i--) if((<<i)&cha) ans+=dis[y][i],y=f[y][i];

     return ans;

 }

 struct ask{

     int x,y,lca,dis; ask(){x=y=dis=;}

     ask(int xx,int yy){x=xx; y=yy; lca=getlca(x,y); dis=getdis(x,y);}

     friend bool operator <(ask a,ask b){return a.dis<b.dis;}

 }p[M];

 int tag[M]={},smp=,maxn=;

 int dfs(int x,int fa){

     int sum=;

     for(int i=head[x];i;i=e[i].next) if(e[i].u!=fa){

         int cnt=dfs(e[i].u,x);

         if(cnt==smp) maxn=max(maxn,e[i].v);

         sum+=cnt;

     }

     return sum+tag[x];

 }

 int main(){

     //freopen("transport.in","r",stdin);

     //freopen("transport.out","w",stdout);

     int n,m; scanf("%d%d",&n,&m);

     for(int i=;i<n;i++){

         int x,y,z; scanf("%d%d%d",&x,&y,&z);

         add(x,y,z); add(y,x,z);

     }

     dfs(,,);

     for(int i=;i<=m;i++){

         int x,y; scanf("%d%d",&x,&y);

         p[i]=ask(x,y);

     }

     sort(p+,p+m+);

     int l=,r=1e9;

     while(l<r){

         int mid=(l+r)>>; smp=maxn=;

         ask op; op.dis=mid;

         int k=upper_bound(p+,p+m+,op)-p;// k--;

         smp=m-k+;

         if(smp==){r=mid; continue;}

         for(int i=k;i<=m;i++){

             tag[p[i].x]++; tag[p[i].y]++;

             tag[p[i].lca]-=;

         }

         dfs(,);

         for(int i=k;i<=m;i++){

             tag[p[i].x]--; tag[p[i].y]--;

             tag[p[i].lca]+=;

         }

         if(p[m].dis-maxn<=mid) r=mid;

         else l=mid+;

     }

     cout<<l<<endl;

 }