【ural1297】 Palindrome

http://acm.timus.ru/problem.aspx?space=1&num=1297 (题目链接)

题意

　　求最长回文子串

Solution

　　后缀数组论文题

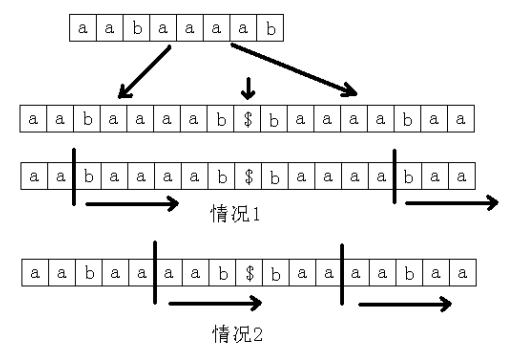
　　穷举每一位，然后计算以这个字符为中心的最长回文子串。注意这里要分两种情况，一是回文子串的长度为奇数，二是长度为偶数。两种情况都可以转化为 求一个后缀和一个反过来写的后缀的最长公共前缀。具体的做法是：将整个字符串反过来写在原字符串后面，中间用一个特殊的字符隔开。这样就把问题变为了求这个新的字符串的某两个后缀的最长公共前缀。如图：

　　感觉后缀数组好像就两个比较有用的操作，一是对height分组，二是将两个串相接并用分隔符隔开。

细节

　　想清楚再写，ST表调了半天。。

代码

// ural1297
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<vector>
#include<cstdio>
#include<cmath>
#include<set>
#define LL long long
#define inf 1<<30
#define Pi acos(-1.0)
#define free(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
using namespace std;

const int maxn=2010;
int rank[maxn],sa[maxn],height[maxn];
int bin[30],st[maxn][30],Log[maxn];
char s[maxn];

namespace Suffix {
	int wa[maxn],wb[maxn],ww[maxn];
	bool cmp(int *r,int a,int b,int l) {
		return r[a]==r[b] && r[a+l]==r[b+l];
	}
	void da(char *r,int *sa,int n,int m) {
		int i,j,p,*x=wa,*y=wb;
		for (i=0;i<=m;i++) ww[i]=0;
		for (i=1;i<=n;i++) ww[x[i]=r[i]]++;
		for (i=1;i<=m;i++) ww[i]+=ww[i-1];
		for (i=n;i>=1;i--) sa[ww[x[i]]--]=i;
		for (p=0,j=1;p<n;j*=2,m=p) {
			for (p=0,i=n-j+1;i<=n;i++) y[++p]=i;
			for (i=1;i<=n;i++) if (sa[i]>j) y[++p]=sa[i]-j;
			for (i=0;i<=m;i++) ww[i]=0;
			for (i=1;i<=n;i++) ww[x[y[i]]]++;
			for (i=1;i<=m;i++) ww[i]+=ww[i-1];
			for (i=n;i>=1;i--) sa[ww[x[y[i]]]--]=y[i];
			for (swap(x,y),p=x[sa[1]]=1,i=2;i<=n;i++)
				x[sa[i]]=cmp(y,sa[i-1],sa[i],j) ? p : ++p;
		}
	}
	void calheight(char *r,int *sa,int n) {
		for (int i=1;i<=n;i++) rank[sa[i]]=i;
		for (int k=0,i=1;i<=n;i++) {
			if (k) k--;
			int j=sa[rank[i]-1];
			while (r[i+k]==r[j+k]) k++;
			height[rank[i]]=k;
		}
	}
}
int query(int x,int y) {
	if (x>y) swap(x,y);x++;
	int k=Log[y-x+1];
	return min(st[x][k],st[y-bin[k]+1][k]);
}
int main() {
	bin[0]=1;for (int i=1;i<=20;i++) bin[i]=bin[i-1]<<1;
	scanf("%s",s+1);
	int n=strlen(s+1);
	s[n+1]='#';
	for (int i=1;i<=n;i++) s[n+i+1]=s[n-i+1];
	n+=n+1;
	Suffix::da(s,sa,n,300);
	Suffix::calheight(s,sa,n);
	for (int i=1;i<=n;i++) st[i][0]=height[i];
	for (int j=1;j<=20;j++)
		for (int i=1;i+bin[j]<=n+1;i++)
			st[i][j]=min(st[i][j-1],st[i+bin[j-1]][j-1]);
	for (int i=2;i<=n;i++) Log[i]=Log[i>>1]+1;
	int l=1,r=1;
	for (int i=1;i<=n/2;i++) {
		int l1=query(rank[i],rank[n-i+1]);
		int l2=query(rank[i+1],rank[n-i+1]);
		if (r-l+1<l1*2-1) l=i-l1+1,r=i+l1-1;
		if (r-l+1<l2*2) l=i-l2+1,r=i+l2;
	}
	for (int i=l;i<=r;i++) printf("%c",s[i]);
    return 0;
}

---

Solution

　　manacher板子题

细节

　　注意数组开两倍，以及刚开始的开始符。下标要想清楚。

代码

// ural1297
#include<algorithm>
#include<iostream>
#include<cstdlib>
#include<cstring>
#include<cstdio>
#include<cmath>
#define LL long long
#define inf 1ll<<60
#define Pi acos(-1.0)
#define free(a) freopen(a".in","r",stdin),freopen(a".out","w",stdout);
using namespace std;

const int maxn=100010;
char s[maxn],st[maxn];
int p[maxn],n;

int Manachar() {
	int len=2;
	st[1]='$';st[2]='#';
	for (int i=1;i<=n;i++) {
		st[++len]=s[i];
		st[++len]='#';
	}
	st[++len]='\0';
	int mx=0,pos=0,id;
	for (int i=1;i<=len;i++) {
		if (i<mx) p[i]=min(p[2*id-i],mx-i);
		else p[i]=1;
		while (st[i-p[i]]==st[i+p[i]]) p[i]++;
		if (mx<i+p[i]) id=i,mx=i+p[i];
		if (p[pos]<p[i]) pos=i;
	}
	return pos;
}
int main() {
	scanf("%s",s+1);
	n=strlen(s+1);
	int k=Manachar();
	for (int i=k-p[k]+1;i<=k+p[k]-1;i++) if (st[i]!='#') printf("%c",st[i]);
	return 0;
}