丽泽普及2022交流赛day17 社论

http://zhengruioi.com/contest/1088

SoyTony 重新 rk1 .

stO SoyTony Orz

省流：俩计数 .

目录

目录

• A
  • 题面
  • 题解
    • Key
    • 算法 1（SoyTony）
    • 算法 2（he_____he）
    • 算法 3
• B
  • 题面
  • 题解
    • 乱搞（artalter）
    • 算法
• C
  • 题面
  • 题解
    • 算法
• D
  • 题面
  • 题解
    • dp
    • Bonus

时间复杂度瞎算的 .

A

题面

一个 \(n\times m\) 的字符矩阵，从左上走到右下，只能往右往下走，问经过路径字典序最小是啥 .

题解

Key

每个字符贪心地走，当且仅当往右和往下字符相同时可能有两种后继状态

算法 1（SoyTony）

BFS .

算法 2（he_____he）

提交记录 .

口胡一下，可能理解错了 .

考虑 dp，由于字符串显然存不下（会 MLE），于是考虑维护排名 .

动态维护排名即可，因为合法的排名不会很多 .

算法 3

等价于 算法 1

按照走的步数枚举算贡献并标记转移点即可 .

B

题面

有 \(n\) 个玻璃杯，每杯里都有水 .

把这 \(n\) 杯里的水互相倒，最终使得只有 \(k\) 个杯子里有水。

易知从把水从第 \(i\) 个玻璃杯倒到第 \(j\) 个花费是 \(c_{i,j}\)，求最小花费。

题解

乱搞（artalter）

首先这个玩意可以按最小生成树走 .

但是这个贪心显然是错的，于是我们钦定两条边然后暴力算最小生成树答案取最优 .

然后……就过了？（

算法

状压 dp，令 \(dp_S\) 表示 \(S\) 集合有水的最小花费，枚举一次倒水即可 .

时间复杂度 \(O(2^nn^2)\) .

C

题面

一张 \(n\) 个点的无向完全图，问边权范围 \(1\sim L\)，且 \(1\to n\) 最短路为 \(k\) 的图数量 .

（BZOJ3868）

题解

算法

显然最短路大于 \(k\) 就没用了，可以直接设为 \(k+1\) .

枚举最短路为 \(s\) 的点数量 \(t_s\)，于是可以钦定一个顺序算一下每个点到 \(1\) 的最短路 \(d\) .

考虑算边权的取值：

• 若 \(d_u=d_v\)，显然 \(w(u,v)\) 取啥都行 .
• 若 \(d_u<d_v\)，则边权不能小于 \(d_v-d_u\)，要不然会破坏最短路 .
• 若 \(d_u>d_v\)，和上面类似 .

那么边权就有 \(L-(d_u-d_v)+1\) 种可能（\(d_u>d_v\)）

但是发现 \(d_u\) 的最短路性质必须要有一个至少一个 \(v\) 来保证 \(d_v + w(v,u) = d_u\)（能取到最短路）.

然而使得那个柿子成立的边权 \(w\) 有 \(L-(d_u-d_v)\) 种可能（如果 \(d_u\ge k\) 这玩意就没贡献了，要丢掉）.

于是目前的总方案数就是

\[ans = \prod(L-(d_u-d_v)+1) - \prod(L-(d_u-d_v))
\]

然而我们枚举的是最短路为 \(s\) 的点数量 \(t_s\)，没有顺序（注意相同数）所以要再乘一个 \((n-2)!/\)，然后因为重复要除以一个 \(\prod a_i\) .

时间复杂度 \(O\left(\dbinom nkn^2\log n\right)\)（抄的别的博客的，存疑）

---

这题真的牛逼，，，

似乎可以说是大力枚举题钓鱼/kx

D

题面

一个 \(n\) 个点的无向图，若满足：

1. 无重边自环
2. 删掉一条边或加上一条边后，满足 \(1\) 且存在一条欧拉回路

则称其是可爱的 .

求 \(n\) 个点可爱图个数，对 \(10^9+7\) 取模 .

两个图不同当且仅当某条边 \((u,v)\) 恰好只存在于某一个图中

题解

dp

显然题目等价于 \(n\) 点欧拉图个数乘上 \(\dbinom n2\) .

令 \(f_n\) 表示 \(i\) 个点的欧拉图数量，\(g_n\) 表示 \(n\) 个点度为偶数的无向图数量 .

众所周知图存在欧拉回路当且仅当没有奇点 .

于是考虑加一个点，容斥掉不连通的

如果原图存在一个欧拉子图，那么 \(i\) 必然要连另外一方面，因为要保持性质，\(i\) 必须连奇点，于是就不连通了（\(i\) 连所有奇点） .

\(g_n\) 显然等于 \(2^{\tbinom{n-1}2}\)（钦定 \(n-1\) 个点随便连，剩下那个点用来平衡奇度点），于是递推式就是

\[f_n=g_n-\sum_{i=1}^{n-1}f_ig_{n-i}\dbinom{n-1}{i-1}
\]

Bonus

zero4338 说 \(f\) 的 EGF 是 \(g_{n-1}\) 的 EGF 的 \(\ln\) .

然后由于神秘的模 \(10^9+7\)，分治 ntt 俩 \(\log\)，MTT 一 \(\log\) .

我打不出代码来验证不了正确性，不过 zero 爷说的话哪里会有错呢？/kx

details .

（众所周知这个 \(g\) 可以 \(O(1)\) 求）

---

我草有原题，叫 建设游乐园，百度能搜到 题解 .

\(\ln\) 的结论是对的，等我变强后看看为啥吧 qwq .

---

zero4338 只说了连通图个数 EGF 是随便图个数 EGF 的 \(\ln\) .

但是这玩意和欧拉图个数有啥关系啊 /yun .

upd. 度数都为偶数的图可以分成若干个欧拉图 —— zero4338

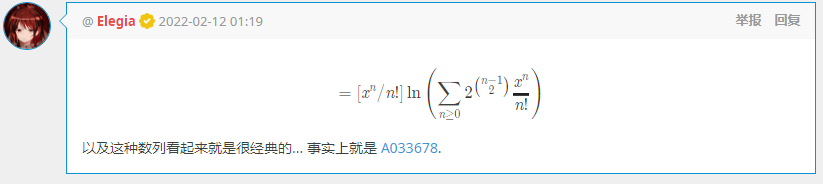
然而 EI 给出了一模一样的式子，并丢了一个 OEIS 序列（我搜不到是因为我第一项错了qwq）：

颤抖，颤抖。