【笔记】CF1251E Voting 及相关

题目传送门

贪心：

一个人 \(i\) 要投票，两种情况：花钱，或当前的人数达到了 \(m_i\)。

而当前达到 \(m_i\) 的话所有 \(m_j \le m_i\) 也就达到要求了。

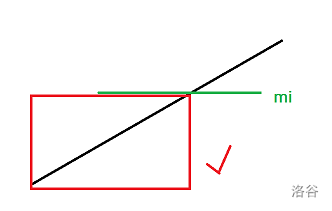
所以考虑将所有人按 \(m\) 从小到大排序。用 \(vetcor\) 当桶。

其次考虑如何贿赂最优。当前如果要达到 \(m_i\)，优先考虑贿赂 \(m\) 更大的。因为贿赂比他小的可以达到的还是 \(m_i\)，贿赂比他大的就可以达到 \(m_i+1\)。同时，后面的要求比前面高，不用再考虑，会更优。

而在比 \(m_i\) 大的所有人中，贪心贿赂 \(p_i\) 更小的显然更好。所以，需要维护比 \(m_i\) 大的所有人中 \(p_i\) 的最小值。考虑用小根堆维护。

堆：

没怎么用过，补

用 \(stl\) 中的优先队列。

小根堆：

priority_queue< 数据类型 ,vector< 数据类型 >,greater< 数据类型 > > q;

大根堆：

priority_queue< 数据类型 > q;

或

priority_queue< 数据类型 ,vector< 数据类型 >,less< 数据类型 > > q;

基本操作：

empty()  //判断一个队列是否为空
pop()  //删除队顶元素
push(x)  //加入一个元素 x
size()  //返回优先队列中拥有的元素个数
top()  //返回优先队列的队顶元素

其存取时间复杂度 \(O(logn)\)

板：

P3378

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,op;
ll x;
priority_queue<ll,vector<ll>,greater<ll> > q;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&op);
		if(op==1){
			scanf("%lld",&x);
			q.push(x);
		}
		else if(op==2) printf("%lld\n",q.top());
		else q.pop();
	}
	return 0;
}

P1334 瑞瑞的木板

将分割看成合成。每次选取两块长度最小的合答案最小。

用小根堆维护当前最小两块板，合完删掉这两块，并加入他们的和。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
int n,a,_1,_2;
ll ans;
priority_queue<int,vector<int>,greater<int> > q;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++){
		scanf("%d",&a);
		q.push(a);
	}
	for(int i=1;i<n;i++){
		_1=q.top(),q.pop();
		_2=q.top(),q.pop();
		q.push(_1+_2);
		ans+=(ll)_1+(ll)_2;
	}
	printf("%lld",ans);
	return 0;
}

双倍经验：合并果子

对顶堆：

对顶堆用于维护第 \(k\) 大的数。

是堆顶相对的一个大根堆和一个小根堆，其中小根堆存较大的一部分数，大根堆存较小的一部分数。大根堆堆顶一般是第 \(k\) 大数。插入：根据需要插到插到大根堆或小根堆，然后调整堆顶。

P1801 黑匣子

用对顶对维护第 \(i\) 大的数。插入到大根堆，若还不到 \(get\) 就把大根堆堆顶调到小根堆。每次 \(get\) 后调整一位堆顶，达到 \(i++\) 的效果。

#include<bits/stdc++.h>
using namespace std;
int n,m,a[200005],u[200005],now;
priority_queue<int> b;
priority_queue<int,vector<int>,greater<int> > s;
int main(){
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<=m;i++) scanf("%d",&u[i]);
	for(int i=1;i<=m;i++){
		while(now<u[i]){
			b.push(a[++now]);
			s.push(b.top());
			b.pop();
		}
		printf("%d\n",s.top());
		b.push(s.top());
		s.pop();
	}
	return 0;
}

P1168 中位数

若当前数 \(>mid\)，则放到小根堆，否则放到大根堆。

每次奇数个都要查询并更新 \(mid\)，所以两个堆的大小差不超过 \(2\)。所以每次奇数个时，判断。若小根堆更大就更新 \(mid\) 为小根堆堆顶，并向大根堆调整。若大根堆更大，就更新 \(mid\) 为大根堆堆顶，并向小根堆调整。若大小相等， \(mid\) 不变。

#include<bits/stdc++.h>
using namespace std;
int n,a,mid;
priority_queue<int> b;
priority_queue<int,vector<int>,greater<int> > s;
int main(){
	scanf("%d%d",&n,&a);
	printf("%d\n",a);
	mid=a;
	for(int i=2;i<=n;i++){
		scanf("%d",&a);
		if(a>mid) s.push(a);
		else b.push(a);
		if(i%2==0) continue;
		if(b.size()>s.size()){
			s.push(mid);
			mid=b.top();
			b.pop();
		}
		else if(b.size()<s.size()){
			b.push(mid);
			mid=s.top();
			s.pop();
		}
		printf("%d\n",mid);
	}
	return 0;
}

重载运算符

用于结构体中的比较。

P1878 舞蹈课

删除后补位，用链表实现。

同时，优先取插值较小的一对，可以用小根堆维护每一对的差值。同时要记录两人的编号，要用结构体。

首先把初始的相邻男女插到堆中，之后每次取堆顶记录答案，取完后标记掉，并更新左右编号（链表）。若出现的新的可行的一对，就再入队，直到队列为空。

重载运算符中，第一关键字为差值，第二关键字为左边人的编号。

#include<bits/stdc++.h>
using namespace std;
int n,a[200005],cnt=0,ans[2][200005];
int l[200005],r[200005],x,y;
bool fl=1,mark[200005];
struct node{
	int w,c,d;
};
bool operator<(node a,node b){
	if(a.w!=b.w) return a.w>b.w;
	else return a.c>b.c;
}
priority_queue<node> q;
string s;
int main(){
	scanf("%d",&n);
	cin>>s;
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<n;i++){
		if(s[i-1]!=s[i]){
			node k;
			k.w=abs(a[i]-a[i+1]),k.c=i,k.d=i+1;
			q.push(k);
		}
	}
	for(int i=1;i<=n;i++) l[i]=i+1,r[i]=i-1;
	while(q.size()){
		node t=q.top();
        q.pop();
		x=t.c,y=t.d;
		if(mark[x]!=0||mark[y]!=0) continue;
		l[r[x]]=l[y];
		r[l[y]]=r[x];
		ans[0][++cnt]=x,ans[1][cnt]=y;
		mark[x]=mark[y]=1;
		if(mark[r[x]]==0&&mark[l[y]]==0){
			if((s[r[x]-1]+s[l[y]-1])==('G'+'B')){
				node k;
				k.w=abs(a[r[x]]-a[l[y]]),k.c=r[x],k.d=l[y];
				q.push(k);
            }
		}
	}
	printf("%d\n",cnt);
	for(int i=1;i<=cnt;i++) printf("%d %d\n",ans[0][i],ans[1][i]);
	return 0;
}

P1631 序列合并

因为两数列按顺序给出，所以可以得到：

不管怎么样，\(A\) 序列中的第一个数绝对要选，那么这个数可能和 \(B\) 序列中的任何一个数组成的数对被选，全部加入优先队列中，这样处理了 \(i,j+1\) 的情况。

还有 \(i+1,j\) 的情况，每次输出一个和之后，将 \(B\) 序列中的第 \(i\) 个数对应的 \(A\) 序列中的第 \(j\) 个数的 \(j++\)，组成数对。

但是这样数对还是容易重复。可以用一个数组记录一下，\(id[i]\) 表示 \(B\) 序列中的第 \(i\) 个数与 \(A\) 序列中的第几个数相加，每次入队的时候累加 \(id\) 数组就不会造成重复了。

用结构体存和与序号。但 priority_queue<node> 是大根堆，而本题需要小根堆。所以重载运算符：

bool operator<(node a,node b){
	return a.v>b.v;
}

将小于强制定义为大于即可。

#include<bits/stdc++.h>
using namespace std;
struct node{
	int v,c;
};
bool operator<(node a,node b){
	return a.v>b.v;
}
priority_queue<node> q;
node k;
int a[100005],b[100005],id[100005],n;
int main(){
	scanf("%d",&n);
	for(int i=1;i<=n;i++) scanf("%d",&a[i]);
	for(int i=1;i<=n;i++){
		scanf("%d",&b[i]);
		id[i]=1;
		k.v=a[1]+b[i],k.c=i;
		q.push(k);
	}
	for(int i=1;i<=n;i++){
		printf("%d ",q.top().v);
		int tmp=q.top().c;
		q.pop();
		k.v=a[++id[tmp]]+b[tmp],k.c=tmp;
		q.push(k);
	}
	return 0;
}

解决：

首先按 \(m\) 的大小，分别放在 \(vector\) 中。

然后 \(i\) 从 \(n-1\) 开始（从大到小），每次先把 \(m\) 值为 \(i\) 的人的贿赂花费放到小根堆中，然后比较堆的大小和 \(n-i\)。若 \(q.size()>n-i\) ，则说明人数不够，就挑堆顶贿赂，直到够了为止。

#include<bits/stdc++.h>
#define ll long long
using namespace std;
ll T,n,p,m,ans;
vector<ll> a[200005];
priority_queue<ll,vector<ll>,greater<ll> > q;
void cl(){
	ans=0;
	for(int i=0;i<=n;i++) a[i].clear();
	while(q.size()) q.pop();
}
void solve(){
	scanf("%lld",&n);
	cl();
	for(int i=1;i<=n;i++){
		scanf("%lld%lld",&m,&p);
		a[m].push_back(p);
	}
	for(int i=n-1;i>=0;i--){
		for(int j=0;j<a[i].size();j++){
			q.push(a[i][j]);
		}
		while(q.size()>n-i){
			ans+=q.top();
			q.pop();
		}
	}
	printf("%lld\n",ans);
	return ;
}
int main(){
	scanf("%lld",&T);
	while(T--) solve();
	return 0;
}