深度学习基础-基于Numpy的多层前馈神经网络（FFN）的构建和反向传播训练

本文是深度学习入门： 基于Python的实现、神经网络与深度学习（NNDL）以及花书的读书笔记。本文将以多分类任务为例，介绍多层的前馈神经网络（Feed Forward Networks，FFN）加上Softmax层和交叉熵CE（Cross Entropy）损失的前向传播和反向传播过程（重点）。本文较长。

一、概述

1.1 多层前馈神经网络

        多层的前馈神经网络又名多层感知机（Multi-Layer Perceptrons, MLP）。MLP只是经验叫法，但实际上FFN不等价于MLP，因为原始的MLP通常使用不可微的阶跃函数，而不是连续的非线性函数。

Figure 1 展示了单层的FFN。当多层的FFN堆叠起来，它就有了深度神经网络的万能近似能力。实际上，两层的FFN或MLP就具备强大的拟合能力。在数据足够多的时候，足够宽的（神经元足够多的）两层网络可以逼近任意连续函数。直观理解，两层的FFN有点类似于一个分段非线性函数， 或者是非线性函数的非线性组合，因而任何连续函数都可以被它表示（值得注意的是，能够表示不一定意味着可以学到这个函数。而且不一定是最优的）。

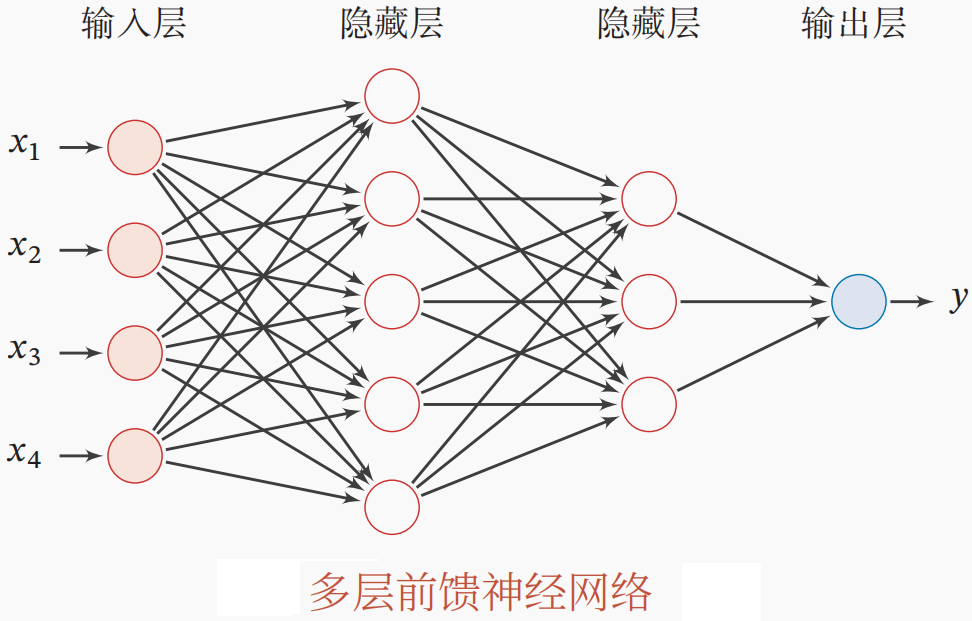
多层的前馈神经网络FFN的结构如上图所示。常用的FFN一般由2层或3层网络构成（不包括输入层）。

此外，单层网络的符号定义和公式如下图所示。一般FFN将采用Relu作为隐藏层的激活函数。

本文中没有给出多层FFN的手动反向传播推导过程。具体可查看NNDL 第93页。手动反向传播主要涉及矩阵求导（本质上是求多变量的偏导数）和链式法则。

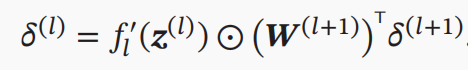
每层FFN中参数的梯度是由当前层的净输入（仿射变换的结果）关于激活函数的梯度、参数关于净输入的梯度（偏导数矩阵-即Jaccobian Matrix）以及上一层传过来的梯度（误差项）连乘所得。值得注意的是，对于深层网络而言，当选用sigmoid或tanh激活函数，由于其容易饱和使梯度较小，而层层的梯度回传会让梯度衰减甚至消失，导致网络难以训练。

多层FFN用于分类的优化目标如下：

1.2 计算图

对于较深的网络，手工推导每一层参数的梯度很繁琐也容易出错。尽管，基于数值微分的自动微分方法（利用泰勒Taylor公式一阶近似，以一阶差分近似微分）可以计算梯度，但此法需要对每一个参数都进行一次前向传播计算，因而十分耗时。在实际中，基于数值微分的梯度计算通常只用于梯度校验。这时就需要利用计算图，依赖链式法则来自动进行梯度反向传播，以求解各个参数的梯度。

计算图中每个输入节点表示变量（标量、向量、矩阵和张量），此外操作也可以表示为节点 （前向传播和反向传播），它详细描绘了每一步的计算过程。计算图可以有效地计算参数的提取，例如重用梯度矩阵。

1、手动实现各个模块的前向和反向计算过程（解耦合），然后把各个模块拼接起来。 缺点就是反向过程也需要手动实现。本文主要介绍此类方法。

2、基于自动计算图的自动微分，可以直接底层实现反向传播，更简便 （这时，可以只专注于网络的搭建）

接下来将，多层FFN和softmax层加loss进行拆分，分别介绍激活函数、仿射变换和softmax-with-loss的计算图，并实现其对应的前向和反向传播。这样，我们就可以将这些层拼接起来，搭建任意深度的神经网络。

1.2.1 激活函数

       1）Sigmoid

Sigmoid激活函数及其计算图如下所示。Sigmoid函数的关于其输入x的梯度可以被简化为y(1-y)。

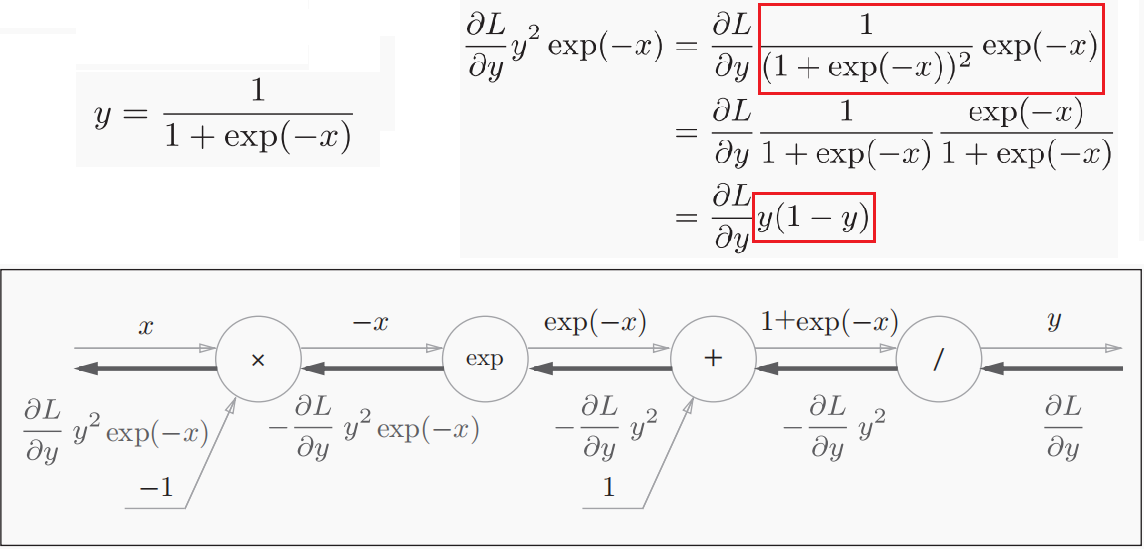
Sigmoid层的代码实现如下。

class Sigmoid:
    def __init__(self):
        self.out = None

    def forward(self, x):
        out = 1 / (1 + np.exp(-x))
        self.out = out
        return out

    def backward(self, dout):
        dx = dout * (1.0 - self.out) * self.out
        return dx

       2）Relu

        如果正向传播时的输入x大于0，则反向传播会将上游的值原封不动地传给下游。反过来，如果正向传播时的x小于等于0，则反向传播中传给下游的信号将停在此处。ReLU层的计算图如下图所示。

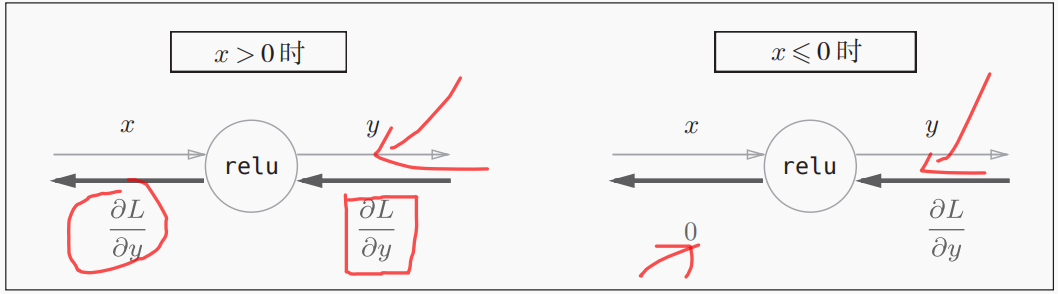
ReLU层的代码实现如下。Relu类有实例变量mask。这个变量mask是由True/False构成的NumPy数组，它会把正向传播时的输入x的元素中小于等于0的地方保存为True，其他地方（大于0的元素）保存为False。dout是上层回传的梯度。

class Relu:
    def __init__(self):
        self.mask = None

    def forward(self, x):
        self.mask = (x <= 0)  # Numpy, True/False
        out = x.copy()
        out[self.mask] = 0
        return out

    def backward(self, dout):
        dout[self.mask] = 0
        dx = dout
        return dx

1.2.2 仿射变换

       神经网络的前向传播中进行的矩阵的乘积运算在几何学领域被称为“仿射变换”，它包括一次线性变换和一次平移，分别对应神经网络的加权和运算与加偏置运算。

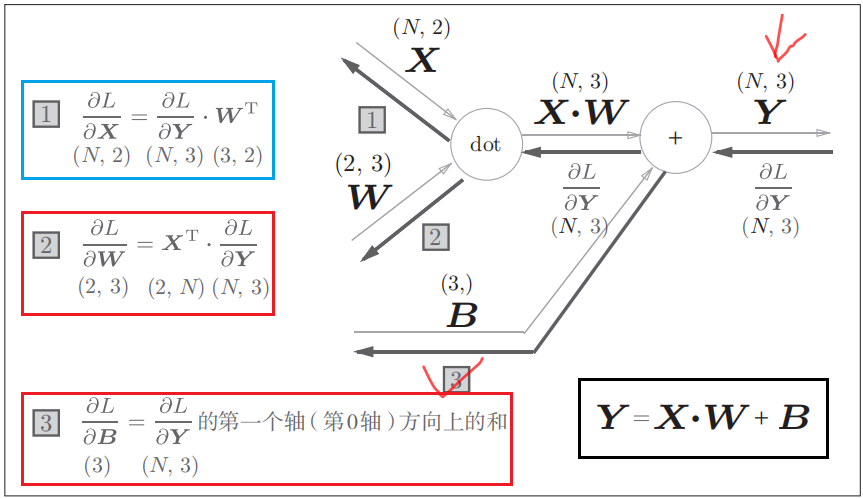
这里我们假设输入是N个样例构成的一个batch。我们可以根据计算图得出仿射变换中关于参数W和偏置B（实际计算中，会对每一个输入加相同的偏置向量，由此构成偏置矩阵。在计算其梯度时，需将每一项梯度求和）。仿射变换层的代码实现如下。

class Affine:
    def __init__(self, W, b):
        self.W = W
        self.b = b
        self.x = None
        self.original_x_shape = None
        self.dW = None # 权重和偏置参数的梯度
        self.db = None

    def forward(self, x):
        self.original_x_shape = x.shape
        x = x.reshape(x.shape[0], -1)
        self.x = x
        out = np.dot(self.x, self.W) + self.b  # Numpy自动广播
        return out

    def backward(self, dout):
        dx = np.dot(dout, self.W.T)  # dout is ∂L/∂Y即上一层的梯度
        self.dW = np.dot(self.x.T, dout)
        self.db = np.sum(dout, axis=0)
        dx = dx.reshape(*self.original_x_shape)  # 还原输入数据的形状（对应张量）
        return dx  # 根据计算图，将当前层的梯度dx向前回传

1.2.3  softmax-with-loss

       例如，在进行手写数字识别时，Softmax层的输出如上图所示。为了便于描述，这里将多分类别数设为3，其计算图如下所示。其中，y代表预测值，而t代表ground truth label。

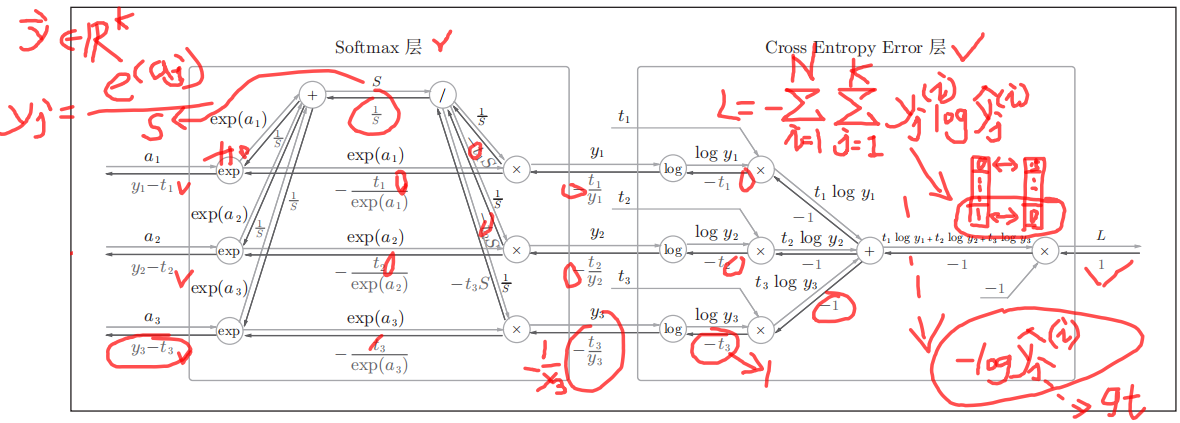
可以看到Softmax层的反向传播得到了（y1 − t1, y2 − t2, y3 − t3）这样“漂亮”的结果。由于（y1, y2, y3）是Softmax层的输出，（t1, t2, t3）是监督数据，所以（y1 − t1, y2 − t2, y3 − t3）是Softmax层的输出和真实标签的差值。神经网络的反向传播会把这个差分表示的误差传递给前面的层，这是神经网络学习中的重要性质。

在多分类中，ground truth label是一个one-hot编码，这意味着真实标签向量中仅有一维为1，而其余维都为0。假设t3为1，而t1、t2皆为0。在基于交叉熵损失优化网络参数时，误差项将以（y1, y2, y3 − 1）反向传播，以调整网络参数。 由上图可知，尽管在实际计算交叉熵损失时，只会计算真实标签向量中真正类别对应维的负对数似然，但是这个损失在反向传播中也会引导网络去调整其他层的参数。

softmax-with-loss层的代码实现如下。

def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T 

    x = x - np.max(x)  # 应对数值溢出的对策，输出与原式等价
    return np.exp(x) / np.sum(np.exp(x))

def cross_entropy_error(y, t):
    if y.ndim == 1:
        t = t.reshape(1, t.size)
        y = y.reshape(1, y.size)

    # 监督数据是one-hot-vector的情况下，转换为正确解标签的索引
    if t.size == y.size:
        t = t.argmax(axis=1)

    batch_size = y.shape[0]
    return -np.sum(np.log(y[np.arange(batch_size), t] + 1e-7)) / batch_size

class SoftmaxWithLoss:
    """ Softmax Layer With Cross Entropy Loss """
    def __init__(self):
        self.loss = None
        self.y = None # softmax的输出
        self.t = None # 监督数据

    def forward(self, x, t):
        self.t = t
        self.y = softmax(x)
        self.loss = cross_entropy_error(self.y, self.t)
        return self.loss

    def backward(self, dout=1):
        batch_size = self.t.shape[0]
        if self.t.size == self.y.size: # 监督数据是one-hot-vector的情况
            dx = (self.y - self.t) / batch_size
        else:
            dx = self.y.copy()
            dx[np.arange(batch_size), self.t] -= 1
            dx = dx / batch_size

        return dx

二、模型构建和训练

依据第一节的实现的激活函数、仿射变换层以及损失，3层FFN的分类模型的前向传播以及反向传播计算梯度的可由如下代码实现。这里可以尝试将Relu替换为Sigmoid函数来查看模型的效果。

import numpy as np
from collections import OrderedDict

class ThreeLayerNet:
    def __init__(self, input_size, hidden_size, output_size, weight_init_std = 0.01):
        print("Build Net")  # 初始化权重
        mid_size = hidden_size // 2
        self.params = {}
        self.params['W1'] = weight_init_std * np.random.randn(input_size, hidden_size)
        self.params['b1'] = np.zeros(hidden_size)
        self.params['W2'] = weight_init_std * np.random.randn(hidden_size, mid_size)
        self.params['b2'] = np.zeros(mid_size)
        self.params['W3'] = weight_init_std * np.random.randn(mid_size, output_size)
        self.params['b3'] = np.zeros(output_size)

        # 生成层
        self.layers = OrderedDict()
        self.layers['Affine1'] = Affine(self.params['W1'], self.params['b1'])
        self.layers['Relu1'] = Relu()
        self.layers['Affine2'] = Affine(self.params['W2'], self.params['b2'])
        self.layers['Relu2'] = Relu()
        self.layers['Affine3'] = Affine(self.params['W3'], self.params['b3'])

        self.lastLayer = SoftmaxWithLoss()

    def predict(self, x):
        for layer in self.layers.values():
            x = layer.forward(x)

        return x

    def loss(self, x, t):
	    # x:输入数据, t:监督数据
        y = self.predict(x)
        return self.lastLayer.forward(y, t)

    def accuracy(self, x, t):
        y = self.predict(x)
        y = np.argmax(y, axis=1)
        if t.ndim != 1 : t = np.argmax(t, axis=1)

        accuracy = np.sum(y == t) / float(x.shape[0])
        return accuracy

    def gradient(self, x, t):
        self.loss(x, t)  # forward

        dout = 1  # backward
        dout = self.lastLayer.backward(dout)

        layers = list(self.layers.values())
        layers.reverse()
        for layer in layers:
            dout = layer.backward(dout)

        grads = {}
        grads['W1'], grads['b1'] = self.layers['Affine1'].dW, self.layers['Affine1'].db
        grads['W2'], grads['b2'] = self.layers['Affine2'].dW, self.layers['Affine2'].db
        grads['W3'], grads['b3'] = self.layers['Affine3'].dW, self.layers['Affine3'].db
        return grads

加载MNIST数据集。

# coding: utf-8
try:
    import urllib.request
except ImportError:
    raise ImportError('You should use Python 3.x')
import os.path
import gzip
import pickle
import os
import numpy as np

url_base = 'http://yann.lecun.com/exdb/mnist/'
key_file = {
    'train_img':'train-images-idx3-ubyte.gz',
    'train_label':'train-labels-idx1-ubyte.gz',
    'test_img':'t10k-images-idx3-ubyte.gz',
    'test_label':'t10k-labels-idx1-ubyte.gz'
}

dataset_dir = os.path.dirname(os.path.abspath(__file__))
save_file = dataset_dir + "/mnist.pkl"

train_num = 60000
test_num = 10000
img_dim = (1, 28, 28)
img_size = 784

def _download(file_name):
    file_path = dataset_dir + "/" + file_name

    if os.path.exists(file_path):
        return

    print("Downloading " + file_name + " ... ")
    urllib.request.urlretrieve(url_base + file_name, file_path)
    print("Done")

def download_mnist():
    for v in key_file.values():
       _download(v)

def _load_label(file_name):
    file_path = dataset_dir + "/" + file_name

    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
            labels = np.frombuffer(f.read(), np.uint8, offset=8)
    print("Done")

    return labels

def _load_img(file_name):
    file_path = dataset_dir + "/" + file_name

    print("Converting " + file_name + " to NumPy Array ...")
    with gzip.open(file_path, 'rb') as f:
            data = np.frombuffer(f.read(), np.uint8, offset=16)
    data = data.reshape(-1, img_size)
    print("Done")

    return data

def _convert_numpy():
    dataset = {}
    dataset['train_img'] =  _load_img(key_file['train_img'])
    dataset['train_label'] = _load_label(key_file['train_label'])
    dataset['test_img'] = _load_img(key_file['test_img'])
    dataset['test_label'] = _load_label(key_file['test_label'])

    return dataset

def init_mnist():
    download_mnist()
    dataset = _convert_numpy()
    print("Creating pickle file ...")
    with open(save_file, 'wb') as f:
        pickle.dump(dataset, f, -1)
    print("Done!")

def _change_one_hot_label(X):
    T = np.zeros((X.size, 10))
    for idx, row in enumerate(T):
        row[X[idx]] = 1

    return T

def load_mnist(normalize=True, flatten=True, one_hot_label=False):
    """读入MNIST数据集

    Parameters
    ----------
    normalize : 将图像的像素值正规化为0.0~1.0
    one_hot_label :
        one_hot_label为True的情况下，标签作为one-hot数组返回
        one-hot数组是指[0,0,1,0,0,0,0,0,0,0]这样的数组
    flatten : 是否将图像展开为一维数组

    Returns
    -------
    (训练图像, 训练标签), (测试图像, 测试标签)
    """
    if not os.path.exists(save_file):
        init_mnist()

    with open(save_file, 'rb') as f:
        dataset = pickle.load(f)

    if normalize:
        for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].astype(np.float32)
            dataset[key] /= 255.0

    if one_hot_label:
        dataset['train_label'] = _change_one_hot_label(dataset['train_label'])
        dataset['test_label'] = _change_one_hot_label(dataset['test_label'])

    if not flatten:
         for key in ('train_img', 'test_img'):
            dataset[key] = dataset[key].reshape(-1, 1, 28, 28)

    return (dataset['train_img'], dataset['train_label']), (dataset['test_img'], dataset['test_label']) 

if __name__ == '__main__':
    init_mnist()

基于SGD对模型进行训练。

import sys, os
sys.path.append(os.pardir)  # 为了导入父目录的文件而进行的设定
import numpy as np
import matplotlib.pyplot as plt
from dataset.mnist import load_mnist

# 读入并划分数据
ratio = 0.1
(x_train, t_train), (x_test, t_test) = load_mnist(normalize=True, one_hot_label=True)
train_size = x_train.shape[0]
valid_size = int(train_size * ratio)
train_size = train_size - valid_size
x_valid = x_train[:valid_size]
t_valid = t_train[:valid_size]
x_train = x_train[valid_size:]
t_train = t_train[valid_size:]

# 构建网络
network = ThreeLayerNet(input_size=784, hidden_size=64, output_size=10)
learning_rate = 0.01

class SGD:
    """随机梯度下降法（Stochastic Gradient Descent）"""
    def __init__(self, lr=0.01):
        self.lr = lr

    def update(self, params, grads):
        for key in params.keys():
            params[key] -= self.lr * grads[key]   # 不同参数W1, ..., Wk有相同学习率

optimizer = SGD(lr=learning_rate)

# 训练和验证
batch_size = 200
iters_num = 5000 # 适当设定循环的次数
iter_per_epoch = max(train_size / batch_size, 1)
train_loss_list, train_acc_list, valid_acc_list = [], [], []
for i in range(iters_num):
    batch_mask = np.random.choice(train_size, batch_size)
    x_batch = x_train[batch_mask]
    t_batch = t_train[batch_mask]
    grad = network.gradient(x_batch, t_batch) # grad = network.numerical_gradient(x_batch, t_batch)
    optimizer.update(network.params, grad)  # 更新参数

    loss = network.loss(x_batch, t_batch)
    train_loss_list.append(loss)
    if i % iter_per_epoch == 0:
        train_acc = network.accuracy(x_train, t_train)
        valid_acc = network.accuracy(x_valid, t_valid)
        train_acc_list.append(train_acc)
        valid_acc_list.append(valid_acc)
        print("train acc, valid acc | " + str(train_acc) + ", " + str(valid_acc))

# 绘制图形 (Train, test)
markers = {'train': 'o', 'valid': 's'}
x = np.arange(len(train_acc_list))
plt.plot(x, train_acc_list, label='train acc')
plt.plot(x, valid_acc_list, label='valid acc', linestyle='--')
plt.xlabel("epochs")
plt.ylabel("accuracy")
plt.ylim(0, 1.0)
plt.legend(loc='lower right')
plt.show()

# 测试
test_acc = network.accuracy(x_test, t_test)
print("test acc | "  + str(test_acc))

　    值得注意的是，可以很容易将上述代码修改为任意深度的前馈神经网络FFN（其代码可参考此处），当然越深并不意味着效果越好。

此外，训练深度神经网络有很多值得注意的Trick，包括初始化网络参数、对激活值进行归一化、正则化、学习率调节、选择合适的优化算法以及设计更好的网络结构（残差连接或跳连接）。