PageRank原理分析

pagerank是将众多网页看成一个有向图，每个页面就是有向图中的节点。计算每个节点的出度和入度。如果一个网站被大量其他的网页引用，那么他就会有更高的pr分数。

原理

对于所有与节点i相连的节点，用他们的pr值除以他们的出度（一个节点可以给多个节点投票，但是投票的权重会被平摊）

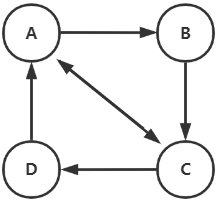
计算转移矩阵。第一列表示A的所有出度 (A->A, A->B, A->C, A->D) ，第一行表示A的所有入度 (A->A, B->A, C->A, D->A) 。

\[M=\left[\begin{array}{llll}
0 & 0 & \frac{1}{2} & 1 \\
\frac{1}{2} & 0 & 0 & 0 \\
\frac{1}{2} & 1 & 0 & 0 \\
0 & 0 & \frac{1}{2} & 0
\end{array}\right]
\]

用矩阵计算来更新pr值：

\[PR_{i}=\sum_{j \in B_{i}} \frac{PR_{j}}{L_{j}}
\]

\[PR(a)=M * P
\]

\[P_{1}=M \cdot P_{0}=\left[\begin{array}{cccc}
0 & 0 & \frac{1}{2} & 1 \\
\frac{1}{2} & 0 & 0 & 0 \\
\frac{1}{2} & 1 & 0 & 0 \\
0 & 0 & \frac{1}{2} & 0
\end{array}\right] \cdot\left[\begin{array}{c}
\frac{1}{4} \\
\frac{1}{4} \\
\frac{1}{4} \\
\frac{1}{4}
\end{array}\right]=\left[\begin{array}{c}
\frac{3}{8} \\
\frac{1}{8} \\
\frac{3}{8} \\
\frac{1}{4}
\end{array}\right]
\]

\(P\)是它们的pr得分， \(L\)是节点的出度。计算下一层pr的方法就是，把相连的节点的pr都拿过来，但是要同时除以他们的出度。pr的默认值就是\(\frac{1}{n}\)

\(0 * \frac{1}{4} + 0 * \frac{1}{4} + \frac{1}{2} * \frac{1}{4} + 1 * \frac{1}{4} = \frac{3}{8}\)

DeadEnds

当一个节点只有入度没有出度，那么他就是DeadEnds。这个节点会导致整个网页的pagerank值趋于0。

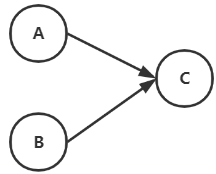
他的转移矩阵M如下，由于他的某一列全为0，导致所有结果都会变成0

\[M=\left[\begin{array}{cccc}
0 & 0 & 0 \\
0 & 0 & 0 \\
1 & 1 & 0 \\
\end{array}\right]
\]

可以看到两轮后就为0了

for i in range(3):
    item = a.dot(item)
    print(item)

# [0. 0. 0.66666667]
# [0. 0. 0.]
# [0. 0. 0.]

修正的方法就是在全为0的那一列加上一个平均值。他的含义就是如果一个页面不链接到任何其他网页，他们他就有可能转换到任何页面。

\[M+a^{T}\left(\frac{e}{n}\right)
\]

• M 是转移矩阵
• a 是 n * n 的向量，如果第i个节点的出度为0，那么a的第i列就全为1，否则就全为0.
• e 是全1的 n * 1 的向量
• 点乘操作（而不是矩阵运算）

其实就是在对应一列加上一个平均值

\[M=\left[\begin{array}{cccc}
0 & 0 & \frac{1}{3} \\
0 & 0 & \frac{1}{3} \\
1 & 1 & \frac{1}{3} \\
\end{array}\right]
\]

SpiderTraps

一个节点只有指向自己的链接，这种节点的权重在迭代的过程中会变成1，而其他的节点会趋于0.

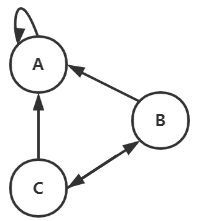
这种节点的转移矩阵如下：

\[M=\left[\begin{array}{cccc}
1 & \frac{1}{2} & \frac{1}{2} \\
0 & 0 & \frac{1}{2} \\
0 & \frac{1}{2} & 0 \\
\end{array}\right]
\]

由于这个节点的对角线元素是1，所以他的pagerank值会不断增加。他的解决方法就是引入一个概率\(\beta\)，用户会有\(\beta\)的概率停留在这个节点，有\(1-\beta\)的概率跳转到其他任何网页。

\[M=\beta M+(1-\beta) \frac{e e^T}{n}
\]

• \(\beta\)是用户留在网页的概率
• e是全一的 n * 1 向量，\(ee^T\)就是全一的 n * n矩阵

这样的话，完整的公式如下所示：

\[PR(a)=\left[\beta\left(M+a^{T}\left(\frac{e}{n}\right)\right)+(1-\beta) \frac{ee^T}{n}\right] * PR
\]

networkx实现

import networkx as nx
import matplotlib.pyplot as plt
import random 

graph = nx.DiGraph()
graph.add_nodes_from(range(0, 100))
for i in range(200):
    m = random.randint(0, 100)
    n = random.randint(0, 100)
    graph.add_edge(m,n)

nx.draw(graph, with_labels=True)
plt.show()

pr = nx.pagerank(graph, max_iter=100, alpha=0.01)
print(pr)