论文解读（GCC）《Graph Contrastive Clustering》

论文信息

论文标题：Graph Contrastive Clustering
论文作者：Huasong Zhong, Jianlong Wu, Chong Chen, Jianqiang Huang, Minghua Deng, Liqiang Nie, Zhouchen Lin, Xian-Sheng Hua
论文来源：2021, ICCV
论文地址：download
论文代码：download

1 Introduction

　　研究方向：解决传统的 URL  没有考虑到类别信息和聚类目标的问题。

　　传统对比学习和本文研究的对比：

　　  

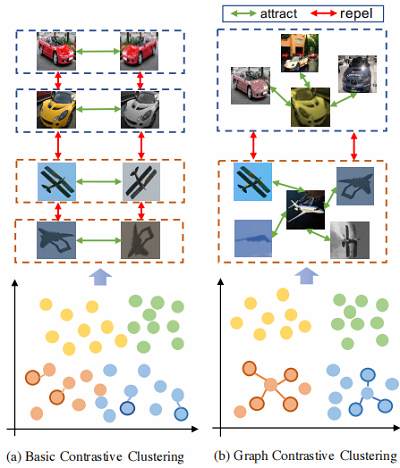
• 传统方式：图及其增强视图为正对；　　
• 本文：一个聚类簇中的视图也应共享相似的特征表示；

2 Method

2.1 Task

　　将 $N$ 个未标记图像通过一个基于CNN 的网络聚类分配为 $K$ 个不同的类：

　　　　$\ell_{i}=\arg  \underset{j}{\text{max}}  \left(p_{i j}\right), 1 \leq j \leq K$

2.2 Graph Contrastive (GC)

　　Symmetric normalized Laplacian：

　　　　$L^{\mathrm{sym}}:=D^{-1 / 2} L D^{-1 / 2}=I-D^{-1 / 2} A D^{-1 / 2}$

　　即：

　　　　$L_{i, j}^{s y m}:=\left\{\begin{array}{ll}1 & \text { if } i=j \text { and } \operatorname{deg}\left(v_{i}\right) \neq 0 \\-\frac{1}{\sqrt{\operatorname{deg}\left(v_{i}\right) \operatorname{deg}\left(v_{j}\right)}} & \text { if } i \neq j \text { and } v_{i} \text { is adjacent to } v_{j} \\0 & \text { otherwise. }\end{array}\right.$

　　【着重观察：$L_{i j}=-\frac{A_{i j}}{\sqrt{d_{i} d_{j}}}, i \neq j$】

　　社区检测中的基本思想： 同一社区中特征表示的相似性应该大于社区之间的相似性。

　　图上的基本思想：邻居之间的表示相似性应该大于非邻居的相似性。

　　社区内（intra-community）的相似性定义为：

　　　　$\mathcal{S}_{i n t r a}=\sum\limits _{L_{i j}<0}-L_{i j} S\left(x_{i}, x_{j}\right)$

　　社区间（inter-community）的相似性定义为：

　　　　$\mathcal{S}_{\text {inter }}=\sum\limits _{L_{i j}=0} S\left(x_{i}, x_{j}\right)$

　　$S\left(x_{i}, x_{j}\right)$ 是相似性函数，本文设置为：

　　　　$S\left(x_{i}, x_{j}\right)=e^{-\left\|x_{i}-x_{j}\right\|_{2}^{2} / \tau} $

　　其中，$\left\|x_{i}-x_{j}\right\|_{2}^{2}=\left\|x_{i}\right\|_{2}^{2}+\left\|x_{j}\right\|_{2}^{2}-2 x_{i} \cdot x_{j}=2-2x_ix_j$          【通常  表示 $\left\|z_{i}\right\|_{2}=1$ (经过正则化)】

　　本文的相似性函数是 $S\left(x_{i}, x_{j}\right)=e^{x_{i} \cdot x_{j} / \tau}$ 。

　　然后，计算 GC 的总损失为：

　　　　$\mathcal{L}_{G C}=-\frac{1}{N} \sum\limits _{i=1}^{N} \log \left(\frac{\sum\limits_{L_{i j}<0}-L_{i j} S\left(x_{i}, x_{j}\right)}{\sum\limits_{L_{i j}=0} S\left(x_{i}, x_{j}\right)}\right)$

　　最小化 $\mathcal{L}_{G C}$ 可以同时增加社区内总相似度，降低社区间总相似度，从而提高可分离性，得到学习得到的特征表示与图结构一致的结果。

2.3 Framework

　　框架如下：

　　

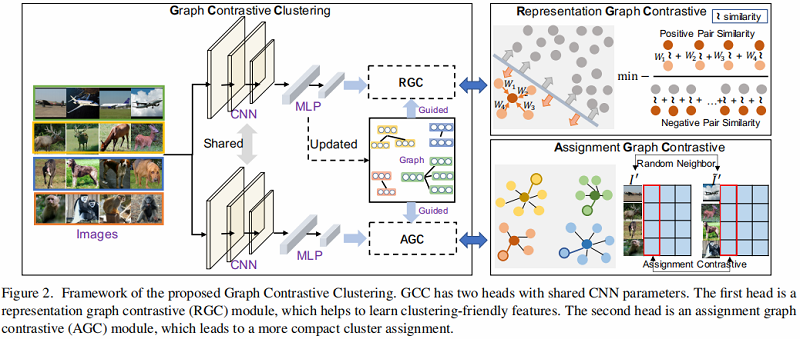
2.3.1 Graph Construction

　　深度模型在训练过程中经常波动，一个 epoch 的特征表示可能有较大的偏差，本文采用移动平均去解决这个问题。

　　假设 $\Phi_{\theta}^{(t)}$ 代表着模型，第 $t$ 个 epoch 的特征表示  $Z^{(t)}=   \left(z_{1}^{(t)}, \cdots, z_{N}^{(t)}\right)=\left(\Phi_{\theta}^{(t)}\left(I_{1}\right), \cdots, \Phi_{\theta}^{(t)}\left(I_{N}\right)\right) $ ，采用的移动平均如下：

　　　　${\large \bar{z}_{i}^{(t)}=\frac{(1-\alpha) \bar{z}_{i}^{(t-1)}+\alpha z_{i}^{(t)}}{\left\|(1-\alpha) \bar{z}_{i}^{(t-1)}+\alpha z_{i}^{(t)}\right\|_{2}}} , i=1, \cdots, N,$

　　其中 $\alpha$ 是权衡参数，$\bar{z}_{i}^{(0)}=z_{i}^{(0)}$ 。

　　然后根据特征表示构造 KNN 图，并计算邻接矩阵：

　　　　$A_{i j}^{(t)}=\left\{\begin{array}{ll}1, & \text { if } \bar{z}_{j}^{(t)} \in \mathcal{N}^{k}\left(\bar{z}_{i}^{(t)}\right) \text { or } \bar{z}_{i}^{(t)} \in \mathcal{N}^{k}\left(\bar{z}_{j}^{(t)}\right) \\0, & \text { otherwise }\end{array}\right. \quad\quad\quad(6)$

　　接着计算其对应的 $L^{\mathrm{sym}}$。

2.3.2 Representation Graph Contrastive

　　在得到 $L^{\mathrm{sym}}$ 后计算 RGC 损失：

　　　　$\mathcal{L}_{R G C}^{(t)}=-\frac{1}{N} \sum\limits _{i=1}^{N} \log {\Large \left(\frac{\sum\limits_{L_{i j}^{(t)}<0}-L_{i j}^{(t)} e^{z_{i}^{\prime} \cdot z_{j}^{\prime} / \tau}}{\sum\limits_{L_{i j}=0} e^{z_{i}^{\prime} \cdot z_{j}^{\prime} / \tau}}\right)} \quad\quad\quad(8)$

2.3.3 Assignment Graph Contrastive

　　传统：image 本身以及其增强 image 应该分配给同一个簇；

　　本文：外加 image 的邻居也应该分配给同一个簇；

　　假设  $I^{\prime}=\left\{I_{1}^{\prime}, \ldots, I_{N}^{\prime}\right\}$  是原始图像 $\mathbf{I}=\left\{I_{1}, \ldots, I_{N}\right\}$ 的随机增强视图。$\tilde{I}^{\prime}=\left\{\tilde{I}_{1}^{\prime}, \ldots, \tilde{I}_{N}^{\prime}\right\} $ 中  $\tilde{I}_{i}^{\prime}$  是  $I_{i}$  根据图邻接矩阵  $A(t)$  选择的随机邻居，$I^{\prime}$  和 $ \tilde{I}^{\prime}$  的概率分配矩阵如下：【行向量角度】

　　　　$\mathbf{p}^{\prime}=\left[\begin{array}{c}p_{1}^{\prime} \\\cdots \\p_{N}^{\prime}\end{array}\right]_{N \times K}$　　　　$\tilde{\mathbf{p}}^{\prime}=\left[\begin{array}{c}p_{\mathrm{RN}\left(I_{1}\right)}^{\prime} \\\cdots \\p_{\mathrm{RN}\left(I_{N}\right)}^{\prime}\end{array}\right]_{N \times K}$

　　其中，$\operatorname{RN}\left(I_{i}\right)$ 表示图像 $I_{i}$ 的一个随机邻居。

　　对上述概率分配矩阵进行转换：【列向量的角度】

　　　　$\mathbf{q}^{\prime}=\left[q_{1}^{\prime}, \quad \ldots \quad, q_{K}^{\prime}\right]_{N \times K}$

　　　　$\tilde{\mathbf{q}}^{\prime}=\left[\tilde{q}_{1}^{\prime}, \quad \cdots \quad, \tilde{q}_{K}^{\prime}\right]_{N \times K}$

　　其中 $q_{i}^{\prime}$ 和 $\tilde{q}_{i}^{\prime}$ 可以告诉我们 $\mathbf{I}^{\prime}$ 和 $\tilde{\mathbf{I}}^{\prime}$ 中的哪些图片将分别被分配给簇 $i$ 。那么我们可以将AGC的学习损失定义为：

　　　　$\mathcal{L}_{A G C}=-\frac{1}{K} \sum\limits _{i=1}^{K} \log \left({\Large \frac{e^{q_{i}^{\prime} \cdot \tilde{q}_{i}^{\prime} / \tau}}{\sum _{j=1}^{K} e^{q_{i}^{\prime} \cdot \tilde{q}_{j}^{\prime} / \tau}} }\right)\quad\quad\quad(9)$

2.3.4 Cluster Regularization Loss

　　在深度聚类中，很容易陷入局部最优解，将大多数样本分配到少数聚类中。为了避免简单的解决方案，我们还添加了一个类似于 PICA[16] 和 SCAN[33] 的聚类正则化损失：

　　　　$\mathcal{L}_{C R}=\log (K)-H(\mathcal{Z})\quad\quad\quad(10)$

　　其中，$H$ 是熵函数，${\large \mathcal{Z}_{i}=\frac{\sum_{j=1}^{N} q_{i j}}{\sum _{i=1}^{K} \sum_{j=1}^{N} q_{i j}}} $，$\mathbf{q}=\left[q_{1}, \cdots, q_{K}\right]_{N \times K}$ 是 $\mathbf{I}$ 的分配概率。

　　那么GCC的总体目标函数可以表述为：

　　　　$\mathcal{L}=\mathcal{L}_{R G C}+\lambda \mathcal{L}_{A G C}+\eta \mathcal{L}_{C R}\quad\quad\quad(11)$

　　其中，$ \lambda$  和 $\eta$  是权重参数。

2.4 Model Training

　　训练过程如下：

　　 

3 Experiments

　　实验结果

　　

相关论文

基于 reconstruction 的深度聚类方法：[39, 28, 8, 11, 40]
基于 self-augmentation 的深度聚类方法：[3, 36, 17, 12, 16, 33, 44]
经典的聚类算法：[43, 10, 2, 35, 37]
谱聚类：[26]
子空间聚类：[24, 9]
深度自适应聚类：[3]
深度综合相关挖掘：[36]
聚类正则化：PICA [16]、SCAN [33]