bzoj1002题解

【题意分析】

　　给你一张特殊的，被称为“轮状基”的无向图，求其生成树个数。

【解题思路】

引理：

　　基尔霍夫矩阵：

基尔霍夫矩阵=度数矩阵-邻接矩阵（邻接矩阵权=两点连边数）

　　Matrix-Tree定理：

对于任意一个无向图，其生成树个数为其基尔霍夫矩阵的任意一个余子式的行列式值。

算法一：

　　直接暴力构图，用Matrix-Tree定理算出生成树个数，复杂度O(n³)，理论可过，但考虑到高精度。。

　　附上一个算矩阵行列式的小公举工具。

算法二：

　　听说这个图很特殊，那一定有一些特殊性质？

　　先写出这个基尔霍夫矩阵的一般形态：

　　答案就是他的任意一个代数余子式的行列式值，为了最简化问题，我们可以去掉第一行第一列：

　　那么只要求这个矩阵的行列式值就可以了。

　　我们先初等变换一下：

　　这样答案就等于这个矩阵的行列式值前面加个符号，即乘上(-1)^n-1

　　寻找这个矩阵行列式计算的规律，发现对倒数第二行进行高斯消元：

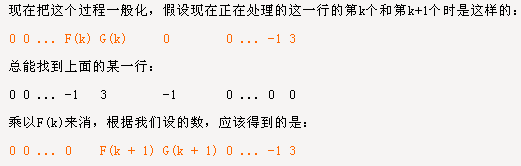
　　可得递推式组：

F_i=G_i-1+3*F_i-1
G_i=-F_i-1

　　整理后即F_i=3*F_i-1-F_i-2(边界F₁=-1,F₂=-3)

　　于是可以矩阵可以变换为这种形式：

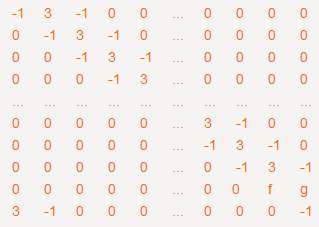
　　同理，对倒数第一行进行高斯消元，矩阵最终变为：

　　其行列式为：(-1)^n-2*f*(i-g*h/f)=(-1)^n-2*(f*i-g*h)

　　则原行列式值为：(-1)^2n-3*(f*i-g*h)=g*h-f*i

　　带入各函数，结合关于行列式的FH定理，展开得：H_n+F_n-1-2

　　设原式=R_n，可得递推式：R_n=3*R_n-1-R_n-2+2(R₁=2,R₂=5)

　　这就是答案递推式了，复杂度O(n)。

　　恩，更详尽的证明，让vfk带你飞！

算法三：

　　打表找规律！（听说这就是我当初把这题当成高精度练习题的理由）

　　设F_i=3*F_i-2-F_i-4，则当i为奇数时，ans_i=F_i²，当i为偶数时，ans_i=5*F_i²

　　复杂度O(n)

【参考程序】

//听说我写这题时我还没有听说过一个叫做Py的东西。。QAQ

//这个板子还有可能是错的。。QAQ

 #include<cstdio>

 #include<iostream>

 #include<cstring>

 #include<string>

 #include<algorithm>

 #include<stack>

 #define REP(I,start,end) for(int I=start;I<=end;I++)

 #define PER(I,start,end) for(int I=start;I>=end;I--)

 using namespace std;

 long long digiter=100000000ll;

 inline void init(long long initer)

 {

     digiter=initer;

 }

 struct bigNumber

 {

     int len;

     long long num[];

     inline void operator =(long long T)

     {

         memset(num,,sizeof(num));

         len=;

         while(T)

         {

             num[++len]=T%digiter;

             T/=digiter;

         }

     }

     bool positive()

     {

         return len&&num[len]>;

     }

     bool odd()

     {

         return num[]&;

     }

     inline bool operator ==(const bigNumber& T)const

     {

         if(len!=T.len)

             return false;

         REP(i,,len)

             if(num[i]!=T.num[i])

                 return false;

         return true;

     }

     inline bool operator >(const bigNumber& T)const

     {

         if(len<T.len)

             return false;

         if(len>T.len)

             return true;

         PER(i,len,)

         {

             if(num[i]<T.num[i])

                 return false;

             if(num[i]>T.num[i])

                 return true;

         }

         return false;

     }

     inline bool operator >=(const bigNumber& T)const

     {

         if(len<T.len)

             return false;

         if(len>T.len)

             return true;

         PER(i,len,)

         {

             if(num[i]<T.num[i])

                 return false;

             if(num[i]>T.num[i])

                 return true;

         }

         return true;

     }

     inline bool operator <(const bigNumber& T)const

     {

         if(len>T.len)

             return false;

         if(len<T.len)

             return true;

         PER(i,len,)

         {

             if(num[i]>T.num[i])

                 return false;

             if(num[i]<T.num[i])

                 return true;

         }

         return false;

     }

     inline bool operator <=(const bigNumber& T)const

     {

         if(len>T.len)

             return false;

         if(len<T.len)

             return true;

         PER(i,len,)

         {

             if(num[i]>T.num[i])

                 return false;

             if(num[i]<T.num[i])

                 return true;

         }

         return true;

     }

     inline void operator +=(const long long TT)

     {

         long long T=TT;

         int i=;

         while(T)

         {

             num[i]+=T%digiter;

             T/=digiter;

             i++;

         }

         REP(i,,len)

         {

             num[i+]+=num[i]/digiter;

             num[i]%=digiter;

         }

         while(num[len+])

             len++;

     }

     inline void operator -=(const long long TT)

     {

         long long T=TT;

         int i=;

         while(T)

         {

             num[i]-=T%digiter;

             T/=digiter;

             i++;

         }

         REP(i,,len)

             while(num[i]<0ll)

             {

                 num[i+]--;

                 num[i]+=digiter;

             }

         while(len&&num[len]==0ll)

             len--;

     }

     inline void operator *=(const long long T)

     {

         REP(i,,len)

             num[i]*=T;

         REP(i,,len)

         {

             num[i+]+=num[i]/digiter;

             num[i]%=digiter;

         }

         while(num[len+])

         {

             len++;

             num[len+]+=num[len]/digiter;

             num[len]%=digiter;

         }

     }

     inline void operator /=(const long long T)

     {

         long long rest=0ll;

         PER(i,len,)

         {

             rest=rest*digiter+num[i];

             num[i]=rest/T;

             rest%=T;

         }

         while(len&&num[len]==0ll)

             len--;

     }

 }f[],three;

 inline bigNumber operator +(const bigNumber A,const bigNumber B)

 {

     bigNumber C;

     memset(C.num,,sizeof(C.num));

     C.len=max(A.len,B.len);

     REP(i,,C.len)

         C.num[i]=A.num[i]+B.num[i];

     REP(i,,C.len)

     {

         C.num[i+]+=C.num[i]/digiter;

         C.num[i]%=digiter;

     }

     while(C.num[C.len+])

     {

         C.len++;

         C.num[C.len+]+=C.num[C.len]/digiter;

         C.num[C.len]%=digiter;

     }

     return C;

 }

 inline bigNumber operator -(const bigNumber A,const bigNumber B)

 {

     bigNumber C;

     memset(C.num,,sizeof(C.num));

     C.len=max(A.len,B.len);

     REP(i,,C.len)

         C.num[i]=A.num[i]-B.num[i];

     REP(i,,C.len)

         while(C.num[i]<)

         {

             C.num[i+]--;

             C.num[i]+=digiter;

         }

     while(C.len&&C.num[C.len]==)

         C.len--;

     return C;

 }

 inline bigNumber operator *(const bigNumber A,const bigNumber B)

 {

     bigNumber C;

     memset(C.num,,sizeof(C.num));

     C.len=A.len+B.len-;

     REP(i,,A.len)

         REP(j,,B.len)

         {

             C.num[i+j-]+=A.num[i]*B.num[j];

             C.num[i+j]+=C.num[i+j-]/digiter;

             C.num[i+j-]%=digiter;

         }

     while(C.num[C.len+])

     {

         C.len++;

         C.num[C.len+]+=C.num[C.len]/digiter;

         C.num[C.len]%=digiter;

     }

     while(C.num[C.len]==)

         C.len--;

     return C;

 }

 inline long long operator %(const bigNumber A,const long long B)

 {

     long long T=;

     PER(i,A.len,)

         T=(T*digiter+A.num[i])%B;

     return T;

 }

 inline bigNumber gcd(const bigNumber AA,const bigNumber BB)

 {

     bigNumber C,A=AA,B=BB;

     while(B.positive())

     {

         C=A;

         while(C>=B)

             C=C-B;

         A=B;

         B=C;

     }

     return A;

 }

 inline bigNumber sqr(const bigNumber T)

 {

     return T*T;

 }

 inline bigNumber power(const bigNumber A,const int B)

 {

     stack<bool> isODD;

     while(!isODD.empty())

         isODD.pop();

     int tmp=B;

     while(tmp)

     {

         isODD.push(tmp&);

         tmp>>=;

     }

     bigNumber C;

     C=1ll;

     while(!isODD.empty())

     {

         C=sqr(C);

         if(isODD.top())

             C=C*A;

         isODD.pop();

     }

     return C;

 }

 inline bigNumber fact(int n)

 {

     bigNumber ans;

     ans=1ll;

     REP(i,,n)

         ans*=i;

     return ans;

 }

 inline bigNumber max(const bigNumber A,const bigNumber B)

 {

     if(A>B)

         return A;

     return B;

 }

 inline bigNumber min(const bigNumber A,const bigNumber B)

 {

     if(A<B)

         return A;

     return B;

 }

 inline void scan(bigNumber& T)

 {

     memset(T.num,,sizeof(T.num));

     if(digiter==10ll)

     {

         T.len=;

         char ch=getchar();

         while(ch<''||ch>'')

             ch=getchar();

         while(ch>=''&&ch<='')

         {

             T.num[++T.len]=ch-'';

             ch=getchar();

         }

         REP(i,,T.len>>)

             swap(T.num[i],T.num[T.len-i+]);

     }

     else

     {

         string st;

         cin>>st;

         T.len=;

         long long tmp=1ll;

         PER(i,st.length()-,)

         {

             T.num[T.len]+=(st[i]-'')*tmp;

             tmp*=10ll;

             if(tmp==digiter)

             {

                 T.len++;

                 tmp=1ll;

             }

         }

         if(tmp==1ll)

             T.len--;

     }

 }

 inline void print(const bigNumber T)

 {

     if(T.len==)

     {

         putchar('');

         return;

     }

     if(digiter==10ll)

         PER(i,T.len,)

             putchar(char(T.num[i])+'');

     else

     {

         printf("%lld",T.num[T.len]);

         PER(i,T.len-,)

         {

             long long tmp=digiter/10ll;

             while(tmp)

             {

                 printf("%lld",T.num[i]/tmp%10ll);

                 tmp/=10ll;

             }

         }

     }

 }

 int n;

 int main()

 {

     scanf("%d",&n);

     f[]=1ll;

     f[]=1ll;

     f[]=4ll;

     f[]=3ll;

     three=3ll;

     REP(i,,n)

         f[i]=f[i-]*three-f[i-];

     f[n]=sqr(f[n]);

     if(~n&)

         f[n]*=5ll;

     print(f[n]);

     return ;

 }

　　和Py比较一下。。

 if __name__=="__main__":

     n,last,ans=input(),1,5

     if n<2:

         print 2

     else:

         for i in xrange(n-2):

             ans,last=3*ans-last+2,ans

         print ans

QAQ

bzoj1002题解的更多相关文章

【BZOJ1002】[ZJOI2006]轮状病毒
[BZOJ1002]轮状病毒题面 bzoj 题解统计个数显然直接矩阵树定理,找规律截这里打标如下: #include <iostream> #include <cstdlib& ...
BZOJ1002【FJOI2007】轮状病毒
1002: [FJOI2007]轮状病毒 Time Limit: 1 Sec Memory Limit: 162 MBSubmit: 6917 Solved: 3777[Submit][Statu ...
bzoj1002 生成树计数找规律
这道题第一眼是生成树计数,n是100,是可以用O(n^3)的求基尔霍夫矩阵的n-1阶的子矩阵的行列式求解的,但是题目中并没有说取模之类的话,就不好办了. 用高精度?有分数出现. 用辗转相除的思想,让它 ...
2016 华南师大ACM校赛 SCNUCPC 非官方题解
我要举报本次校赛出题人的消极出题!!! 官方题解请戳:http://3.scnuacm2015.sinaapp.com/?p=89(其实就是一堆代码没有题解) A. 树链剖分数据结构板题题目大意:我 ...
noip2016十连测题解
以下代码为了阅读方便,省去以下头文件: #include <iostream> #include <stdio.h> #include <math.h> #incl ...
BZOJ-2561-最小生成树题解（最小割）
2561: 最小生成树(题解) Time Limit: 10 Sec Memory Limit: 128 MBSubmit: 1628 Solved: 786 传送门:http://www.lyd ...
Codeforces Round #353 (Div. 2) ABCDE 题解 python
Problems # Name A Infinite Sequence standard input/output 1 s, 256 MB x3509 B Restoring P ...
哈尔滨理工大学ACM全国邀请赛（网络同步赛）题解
题目链接提交连接:http://acm-software.hrbust.edu.cn/problemset.php?page=5 1470-1482 只做出来四道比较水的题目,还需要加强中等题的训练 ...
2016ACM青岛区域赛题解
A.Relic Discovery_hdu5982 Time Limit: 2000/1000 MS (Java/Others) Memory Limit: 65536/65536 K (Jav ...

随机推荐

在三台服务器，搭建redis三主三从集群
一.资源准备 1.准备三台服务器H1.H2.H3 172.26.237.83 H1 172.26.237.84 H2 172.26.237.85 H3 二.配置服务器 1.在H1服务器设置SSH免密登 ...
php获取微信openid
使用微信接口,无论是自动登录还是微信支付我们首先需要获取的就是openid,获取openid的方式有两种,一种是在关注的时候进行获取,这种订阅号就可以获取的到,第二种是通过网页授权获取,这种获取需要的 ...
bzoj 2084
传送门:http://www.lydsy.com/JudgeOnline/problem.php?id=2084 这道题很容易想到就是一个变种的最长回文字串, 不过回文的规则变成了s[i + p[i] ...
WarUtil
/** *包名:cn.yufu.utils *描述:package cn.yufu.utils; */ package cn.yufu.utils; import java.io.File; impo ...
数据结构和算法设计专题之---二分查找(Java版)
1.前提:二分查找的前提是需要查找的数组必须是已排序的,我们这里的实现默认为升序 2.原理:将数组分为三部分,依次是中值(所谓的中值就是数组中间位置的那个值)前,中值,中值后:将要查找的值和数组的中值 ...
Hbase集群类型|集群配置|服务器选型|磁盘容量规划
HBase和Hadoop的集群类型 1.单机模式主要用于开发工作,一台机器上运行所有的守护进程,或者一台机器运行多个虚拟机.一般用于评估和测试. 2.小型集群 20台机器以内的集群,不同的机器运行不 ...
（转）OpenFire源码学习之七：组（用户群）与花名册（用户好友）
转:http://blog.csdn.net/huwenfeng_2011/article/details/43413651 Group 在openfire中的gorop——组,也可以理解为共享组.什 ...
STM32嵌入式开发学习笔记（七）：串口通信（下）
下面我们进行几个串口通信的实际应用. 实验一:发信实验,让开发板通过串口向电脑发送信息: #include <stdio.h> #include <stm32f10x.h> # ...
ASP.NET Core学习——5
日志(Logging)ASP.NET Core内建支持日志,也允许开发人员轻松切换为他们想用的其他日志框架. 通过dependency-injection请求ILoggerFactory或ILogge ...
vscode eslint插件对vue文件无效
vscode配置好了之后,只对.js文件提示 vue文件没有效果改成如下配置就好了. "eslint.validate": [ "javascript", & ...

bzoj1002题解

bzoj1002题解的更多相关文章

随机推荐

热门专题