The Preliminary Contest for ICPC Asia Shanghai 2019 C Triple（FFT+暴力）

The Preliminary Contest for ICPC Asia Shanghai 2019 C Triple（FFT+暴力）

传送门：https://nanti.jisuanke.com/t/41400

题意：

给你三个数组a，b，c，要你求有多少个三元组（i，j，k），使得

\[\begin{array}{l}{\left|A_{i}-B_{j}\right| \leq C_{k}, \text { and }} \\ {\left|B_{j}-C_{k}\right| \leq A_{i}, \text { and }} \\ {\left|A_{i}-C_{k}\right| \leq B_{j}}\end{array}
\]

题解：

上面的不等式经过化简，我们可以得到

我们需要求有多少个三元组，使得\(A_i,B_j,C_k\)可以组成一个三角形

这样组成三角形的题目类似于HDU4609 (https://www.cnblogs.com/buerdepepeqi/p/11236100.html)

但是不同的是 我们需要从三个数组中选择

所以这里就涉及到了选择重复的问题，我们考虑去重

假设拿a+b做一遍卷积，得到长度为a+b的木棍的数量，

我们假设 c是三角形的最长边，那么a，b，c三根木棍不能组成三角形的情况就是c的长度大于a+b的数量

我们枚举（a+b）这个长度，那么不能组成三角形的数量就是 可以组成当前长度的（a，b）的方案数*大于这个长度的c的数量

所以按照这样来说 我们就可以得到 做三遍卷积，分别枚举c为最长边时，b为最长边时， a为最长边时 不和法的数量，然后用所有的三元组的数量减去不合法的三元组的数量就是合法的三元组的数量

这里有一个小技巧，就是小范围暴力？？如果小范围不暴力你就会T

（留恋一下机房惨案

我们来分析一下为什么？

我们假设FFT的Complex类带了一个常数 x

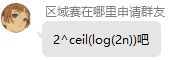
在T是100的情况下，我们单纯的跑三遍FFT，那么就是三遍正的FFT，三遍IDFT，那么就是6的一个常数

复杂度最后就是

\[T*2^{log(2n)}*log(2n)*6*x\\
=100*2^{18}*18*6=2,831,155,200‬
\]

然而暴力的复杂度是n2

假设有20组大数据 80组小数据（1000）

那么复杂度就是

\[20*18*2^{18}*6+1000*1000*80=646,231,040
\]

所以 小范围暴力 大范围FFT的复杂度是比较优秀滴

（感谢NE大佬对于复杂度的分析

代码：

/**
 *　　　　　　　　┏┓　　 　┏┓
 * 　　　　　　　┏┛┗━━━━━━━┛┗━━━┓
 * 　　　　　　　┃　　　　　　　┃ 　
 * 　　　　　　　┃　　　━　　 　┃
 * 　　　　　　　┃　＞　　　＜　┃
 * 　　　　　　　┃　　　　　　　┃
 * 　　　　　　　┃...　⌒　... 　┃
 * 　　　　　　　┃　　　　　　　┃
 * 　　　　　　　┗━┓　　　┏━┛
 * 　　　　　　　　　┃　　　┃　Code is far away from bug with the animal protecting　　　　　　　　　　
 * 　　　　　　　　　┃　　　┃   神兽保佑,代码无bug
 * 　　　　　　　　　┃　　　┃　　　　　　　　　　　
 * 　　　　　　　　　┃　　　┃  　　　　　　
 * 　　　　　　　　　┃　　　┃
 * 　　　　　　　　　┃　　　┃　　　　　　　　　　　
 * 　　　　　　　　　┃　　　┗━━━┓
 * 　　　　　　　　　┃　　　　　　　┣┓
 * 　　　　　　　　　┃　　　　　　　┏┛
 * 　　　　　　　　　┗┓┓┏━┳┓┏┛
 * 　　　　　　　　　　┃┫┫　┃┫┫
 * 　　　　　　　　　　┗┻┛　┗┻┛
 */
// warm heart, wagging tail,and a smile just for you!
//
//                            _ooOoo_
//                           o8888888o
//                           88" . "88
//                           (| -_- |)
//                           O\  =  /O
//                        ____/`---'\____
//                      .'  \|     |//  `.
//                     /  \|||  :  |||//  \
//                    /  _||||| -:- |||||-  \
//                    |   | \  -  /// |   |
//                    | \_|  ''\---/''  |   |
//                    \  .-\__  `-`  ___/-. /
//                  ___`. .'  /--.--\  `. . __
//               ."" '<  `.___\_<|>_/___.'  >'"".
//              | | :  `- \`.;`\ _ /`;.`/ - ` : | |
//              \  \ `-.   \_ __\ /__ _/   .-` /  /
//         ======`-.____`-.___\_____/___.-`____.-'======
//                            `=---='
//        ^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^^
//                     佛祖保佑      永无BUG
#include <set>
#include <map>
#include <stack>
#include <cmath>
#include <queue>
#include <cstdio>
#include <string>
#include <vector>
#include <cstring>
#include <iostream>
#include <algorithm>
using namespace std;
typedef long long LL;
typedef pair<int, int> pii;
typedef unsigned long long uLL;
#define ls rt<<1
#define rs rt<<1|1
#define lson l,mid,rt<<1
#define rson mid+1,r,rt<<1|1
#define bug printf("*********\n")
#define FIN freopen("input.txt","r",stdin);
#define FON freopen("output.txt","w+",stdout);
#define IO ios::sync_with_stdio(false),cin.tie(0)
#define debug1(x) cout<<"["<<#x<<" "<<(x)<<"]\n"
#define debug2(x,y) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<"]\n"
#define debug3(x,y,z) cout<<"["<<#x<<" "<<(x)<<" "<<#y<<" "<<(y)<<" "<<#z<<" "<<z<<"]\n"
const int maxn = 5e5 + 5;
const int INF = 0x3f3f3f3f;
const int mod = 1e9 + 7;
const double Pi = acos(-1);
LL gcd(LL a, LL b) {
    return b ? gcd(b, a % b) : a;
}
LL lcm(LL a, LL b) {
    return a / gcd(a, b) * b;
}
double dpow(double a, LL b) {
    double ans = 1.0;
    while(b) {
        if(b % 2)ans = ans * a;
        a = a * a;
        b /= 2;
    } return ans;
}
LL quick_pow(LL x, LL y) {
    LL ans = 1;
    while(y) {
        if(y & 1) {
            ans = ans * x % mod;
        } x = x * x % mod;
        y >>= 1;
    } return ans;
}

LL res[maxn << 2], len;
struct Complex {
    double r, i;

    Complex(double r = 0, double i = 0) : r(r), i(i) {};

    Complex operator+(const Complex &rhs) {
        return Complex(r + rhs.r, i + rhs.i);
    }

    Complex operator-(const Complex &rhs) {
        return Complex(r - rhs.r, i - rhs.i);
    }

    Complex operator*(const Complex &rhs) {
        return Complex(r * rhs.r - i * rhs.i, i * rhs.r + r * rhs.i);
    }
} va[maxn << 2], vb[maxn << 2];

void rader(Complex F[], int len) { //len = 2^M,reverse F[i] with  F[j] j为i二进制反转
    int j = len >> 1;
    for (int i = 1; i < len - 1; ++i) {
        if (i < j) swap(F[i], F[j]);  // reverse
        int k = len >> 1;
        while (j >= k) {
            j -= k;
            k >>= 1;
        }
        if (j < k) j += k;
    }
}

void FFT(Complex F[], const int &len, const int &t) {
    rader(F, len);
    for (int h = 2; h <= len; h <<= 1) {
        Complex wn(cos(-t * 2 * Pi / h), sin(-t * 2 * Pi / h));
        for (int j = 0; j < len; j += h) {
            Complex E(1, 0); //旋转因子
            for (int k = j; k < j + h / 2; ++k) {
                Complex u = F[k];
                Complex v = E * F[k + h / 2];
                F[k] = u + v;
                F[k + h / 2] = u - v;
                E = E * wn;
            }
        }
    }
    if (t == -1)   //IDFT
        for (int i = 0; i < len; ++i)
            F[i].r /= len;
}

void Conv(Complex a[], Complex b[], const int &len) { //求卷积
    FFT(a, len, 1);
    FFT(b, len, 1);
    for (int i = 0; i < len; ++i) a[i] = a[i] * b[i];
    FFT(a, len, -1);
}

void work() {
    Conv(va, vb, len);
    for (int i = 0; i < len; ++i)res[i] = va[i].r + 0.5;
}
int a[maxn], b[maxn], c[maxn];
int numa[maxn], numb[maxn], numc[maxn];
int suma[maxn], sumb[maxn], sumc[maxn];//长度为i的数量
LL resab[maxn], resbc[maxn], resac[maxn];//长度为i的 a，b的个数
int main() {
#ifndef ONLINE_JUDGE
    FIN
#endif
    int T;
    int cas = 1;
    scanf("%d", &T);
    while(T--) {
        int n;
        scanf("%d", &n);
        int maxlena = 0, maxlenb = 0, maxlenc = 0;
        for(int i = 1; i <= n; i++) {
            scanf("%d", &a[i]);
            numa[a[i]]++;
            maxlena = max(maxlena, a[i]);
        }
        for(int i = 1; i <= n; i++) {
            scanf("%d", &b[i]);
            numb[b[i]]++;
            maxlenb = max(maxlenb, b[i]);

        }
        for(int i = 1; i <= n; i++) {
            scanf("%d", &c[i]);
            numc[c[i]]++;
            maxlenc = max(maxlenc, c[i]);
        }
        LL ans = 1ll * n * n * n;
        if(n <= 1000) {
            for(int i = 1; i <= maxlena; i++) {
                suma[i] = suma[i - 1] + numa[i];
            }
            for(int i = 1; i <= maxlenb; i++) {
                sumb[i] = sumb[i - 1] + numb[i];
            }
            for(int i = 1; i <= maxlenc; i++) {
                sumc[i] = sumc[i - 1] + numc[i];
            }
            for(int i = 1; i <= n; i++) {
                for(int j = 1; j <= n; j++) {
                    resab[a[i] + b[j]]++;
                    resbc[b[i] + c[j]]++;
                    resac[a[i] + c[j]]++;
                }
            }
            int mx = max(maxlena, max(maxlenb, maxlenc));
            for(int i = 1; i <= mx; i++) {
                if(i <= maxlenc) ans -= resab[i] * (sumc[maxlenc] - sumc[i]);
                if(i <= maxlenb) ans -= resac[i] * (sumb[maxlenb] - sumb[i]);
                if(i <= maxlena) ans -= resbc[i] * (suma[maxlena] - suma[i]);
            }
            memset(suma, 0, sizeof(int) * (maxlena + 2));
            memset(sumb, 0, sizeof(int) * (maxlenb + 2));
            memset(sumc, 0, sizeof(int) * (maxlenc + 2));
            memset(numa, 0, sizeof(int) * (maxlena + 2));
            memset(numb, 0, sizeof(int) * (maxlenb + 2));
            memset(numc, 0, sizeof(int) * (maxlenc + 2));
            memset(resac, 0, sizeof(LL) * (mx * 2 + 2));
            memset(resab, 0, sizeof(LL) * (mx * 2 + 2));
            memset(resbc, 0, sizeof(LL) * (mx * 2 + 2));
        } else {
            maxlena++, maxlenb++, maxlenc++;
            len = 1;
            int mxab = max(maxlena, maxlenb);
            while(len < 2 * mxab) len <<= 1;
            for(int i = 0; i < len; i++) {
                if (i < mxab) {
                    va[i] = Complex(numa[i], 0);
                    vb[i] = Complex(numb[i], 0);
                } else
                    va[i] = vb[i] = Complex(0, 0);
            }
            work();
            for (int i = 0; i < len; i++) resab[i] = res[i];

            len = 1;
            int mxac = max(maxlena, maxlenc);
            while(len < 2 * mxac) len <<= 1;
            for(int i = 0; i < len; i++) {
                if (i < mxac) {
                    va[i] = Complex(numa[i], 0);
                    vb[i] = Complex(numc[i], 0);
                } else
                    va[i] = vb[i] = Complex(0, 0);
            }
            work();
            for (int i = 0; i < len; i++) resac[i] = res[i];

            len = 1;
            int mxbc = max(maxlenb, maxlenc);
            while(len < 2 * mxbc) len <<= 1;
            for(int i = 0; i < len; i++) {
                if (i < mxbc) {
                    va[i] = Complex(numb[i], 0);
                    vb[i] = Complex(numc[i], 0);
                } else
                    va[i] = vb[i] = Complex(0, 0);
            }
            work();
            for (int i = 0; i < len; i++) resbc[i] = res[i];

            for(int i = 1; i <= maxlena; i++) {
                suma[i] = suma[i - 1] + numa[i];
            }
            for(int i = 1; i <= maxlenb; i++) {
                sumb[i] = sumb[i - 1] + numb[i];
            }
            for(int i = 1; i <= maxlenc; i++) {
                sumc[i] = sumc[i - 1] + numc[i];
            }

            for (int i = 1; i <= 2 * mxab; ++i) {
                if (i > maxlenc) break;
                ans -= resab[i] * (sumc[maxlenc] - sumc[i]);
            }
            for (int i = 1; i <= 2 * mxbc; ++i) {
                if (i > maxlena) break;
                ans -= resbc[i] * (suma[maxlena] - suma[i]);
            }
            for (int i = 1; i <= 2 * mxac; ++i) {
                if (i > maxlenb) break;
                ans -= resac[i] * (sumb[maxlenb] - sumb[i]);
            }
            memset(suma, 0, sizeof(int) * (maxlena + 2));
            memset(sumb, 0, sizeof(int) * (maxlenb + 2));
            memset(sumc, 0, sizeof(int) * (maxlenc + 2));
            memset(numa, 0, sizeof(int) * (maxlena + 2));
            memset(numb, 0, sizeof(int) * (maxlenb + 2));
            memset(numc, 0, sizeof(int) * (maxlenc + 2));
            memset(resac, 0, sizeof(LL) * (mxac * 2 + 2));
            memset(resab, 0, sizeof(LL) * (mxab * 2 + 2));
            memset(resbc, 0, sizeof(LL) * (mxbc * 2 + 2));
        }
        printf("Case #%d: %lld\n", cas++, ans);
    }
    return 0;
}