HDU 6631 line symmetric 计算几何

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=6631

题意：共\(T\)组数据，每组数据给出\(n\)个点的坐标，这\(n\)个点按顺序给出，相邻的点相连后构成一个简单多边形。询问能否在最多移动一个点的情况下新构成的图形为轴对称图形。

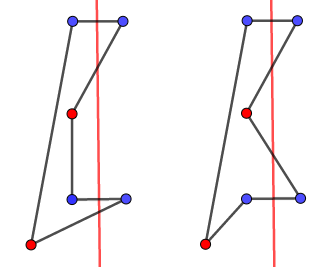
分析：如下图所示，一个轴对称图形的对称轴仅存在两种情况，一是相邻两点的中垂线，二是相隔一点的中垂线。

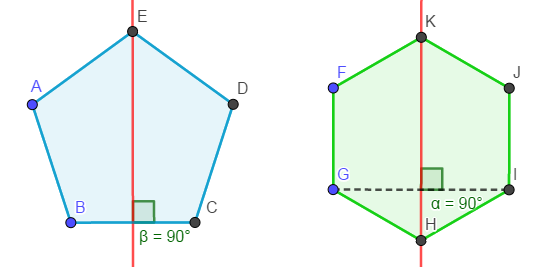
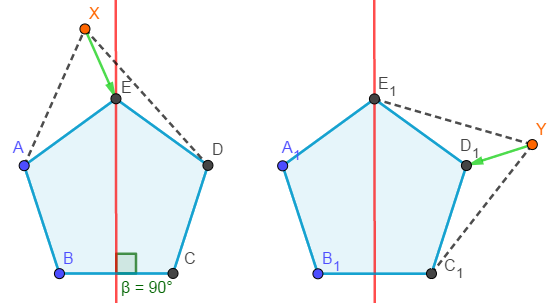
因此我们只需要对相邻点和相隔一点的点对求中垂线，分别判断是否能够仅移动一个点使得图形成为轴对称图形即可。如下图，多边形\(ABCDX\)可以转变为\(ABCDE\)，多边形\(A_1B_1C_1YE_1\)可以转变为\(A_1B_1C_1D_1E_1\)。因此判定能否构成轴对称图形的条件即为轴线两侧的对应点对不关于轴线对称的数量是否\(<2\)。如下图的\(ABCDX\)仅具有一组点对\((X,X)\)不对称。

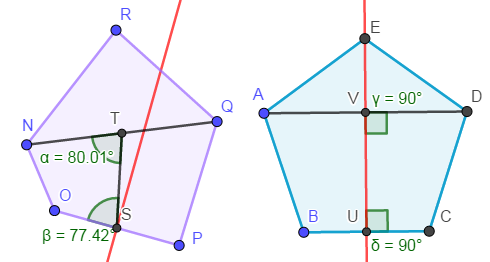
接下来我们需要解决的问题就是如何快速判定点对关于中垂线对称。如下图，若点对关于轴线对称，则必有两组点对的中点连线与这两组点的连线相互垂直。如下图若点\(N,Q\)关于点\(O,P\)形成的中垂线对称，则应有\(ST\bot NQ\)以及\(TS\bot OP\)（\(T\)，\(S\)分别为中点）。

于是我们就得到了一个\(o(n^2)\)的解法，本题就轻松解决了。（大雾）

事实上这样是无法通过的，因为我们忽略了图形有可能自交的情况。如下图样例。

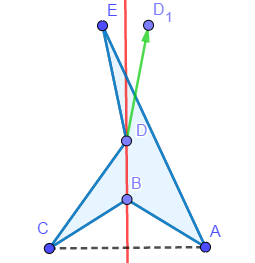
如图，\((D, E)\)点对不构成对称，若将\(D\)点移至\(D_1\)点，则该多边形自交，不再构成简单多边形。因此我们在点对不对称时需要加上特判。特判的方法可由下图观察得到：

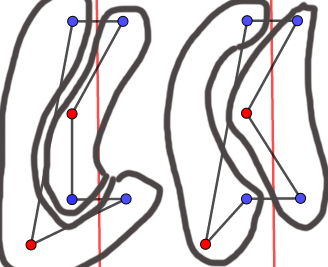
我们以对称轴为界将多边形分成两部分。观察不对称的点对（红点），并且将红点与它相邻的两个点看作一个整体，当且仅当这两组点都跨过对称轴时多边形自交（跨过对称轴包括红点落在对称轴上的情况）。

　

AC代码：

#include <bits/stdc++.h>
#define SIZE 1007
#define rep(i, a, b) for(int i = a; i <= b; ++i)
using namespace std;
typedef long long ll;
int t, n;
struct Point {
	double x, y;
}p[SIZE], a, b, tp, mid, mx, mid2, nullp;
void io() {
	ios::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);
}
double cross(Point a, Point b, Point c) { return (b.x - a.x) * (c.y - b.y) - (b.y - a.y) * (c.x - b.x); }
double cdot(Point a, Point b, Point c) { return (b.x - a.x) * (b.x - c.x) + (b.y - c.y) * (b.y - a.y); }
int spjudge(int j, int k, Point mid, Point mid2) {
	bool f1 = false, f2 = false; int num = 0;
	if (cross(mid, p[j], mid2)) {
		int pre = j - 1, post = j + 1;
		if (pre < 1) pre += n;
		if (post > n) post -= n;
		if (cross(mid, p[pre], mid2)*cross(mid, p[post], mid2) < 0) f1 = true;
		if (cross(mid, p[pre], mid2)*cross(mid, p[j], mid2) < 0) f1 = true;
		if (cross(mid, p[post], mid2)*cross(mid, p[j], mid2) < 0) f1 = true;
	}
	else f1 = true;
	if (cross(mid, p[k], mid2)) {
		int pre = k + 1, post = k - 1;
		if (pre < 1) pre += n;
		if (post > n) post -= n;
		if (cross(mid, p[pre], mid2)*cross(mid, p[post], mid2) < 0) f2 = true;
		if (cross(mid, p[pre], mid2)*cross(mid, p[j], mid2) < 0) f2 = true;
		if (cross(mid, p[post], mid2)*cross(mid, p[j], mid2) < 0) f2 = true;
	}
	else f2 = true;
	if (f1&&f2) return 1;
	else return 0;
}
bool judge1() {
	rep(i, 1, n) {
		int num = 0;
		a = p[i]; b = p[i % n + 1];
		mid.x = (a.x + b.x) / 2; mid.y = (a.y + b.y) / 2;
		mid2.x = mid.x + (a.y - mid.y); mid2.y = mid.y + (mid.x - a.x);
		int tt = n / 2 - 1;
		if (n % 2) {
			tp = p[(i + n / 2) % n + 1];
			if (cross(mid, tp, mid2)) ++num;
		}
		int j = i - 1, k = i + 2;
		while (tt--) {
			if (j < 1) j += n;
			if (k > n) k -= n;
			mx.x = (p[j].x + p[k].x) / 2;
			mx.y = (p[j].y + p[k].y) / 2;
			if ((cdot(p[i], mid, mx) != 0) || (cdot(mid, mx, p[j]) != 0)) {
				++num;
				num += spjudge(j, k, mid, mid2);
			}
			--j, ++k;
		}
		if (num <= 1) return true;
	}
	return false;
}
bool judge2() {
	rep(i, 1, n) {
		int num = 0;
		a = p[i]; b = p[(i + 1) % n + 1];
		mid.x = (a.x + b.x) / 2; mid.y = (a.y + b.y) / 2;
		mid2.x = mid.x + (a.y - mid.y); mid2.y = mid.y + (mid.x - a.x);
		int tt = n / 2 - 1;
		tp = p[i % n + 1];
		if (cross(mid, tp, mid2)) ++num;
		if (n % 2 == 0) {
			tp = p[(i + n / 2) % n + 1];
			if (cross(mid, tp, mid2)) ++num;
		}
		int j = i - 1, k = i + 3;
		while (tt--) {
			if (j < 1) j += n;
			if (k > n) k -= n;
			mx.x = (p[j].x + p[k].x) / 2;
			mx.y = (p[j].y + p[k].y) / 2;
			if ((cdot(p[i], mid, mx) != 0) || (cdot(mid, mx, p[j]) != 0)) {
				++num;
				num += spjudge(j, k, mid, mid2);
			}
			--j, ++k;
		}
		if (num <= 1) return true;
	}
	return false;
}
int main() {
	io(); cin >> t;
	while (t--) {
		cin >> n;
		rep(i, 0, 1000) p[i] = nullp;
		rep(i, 1, n) cin >> p[i].x >> p[i].y;
		if (n < 5) { cout << "Y\n"; continue; }
		if (judge1()) cout << "Y\n";
		else if (judge2()) cout << "Y\n";
		else cout << "N\n";
	}
}