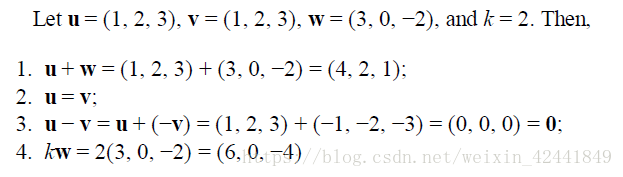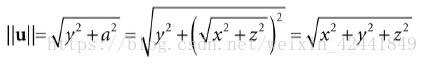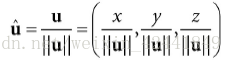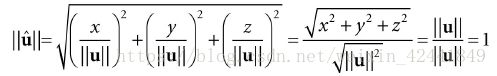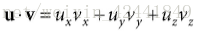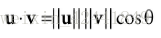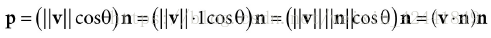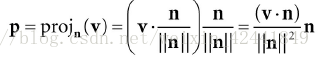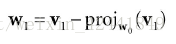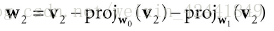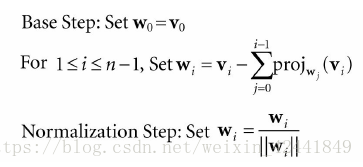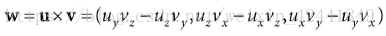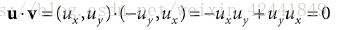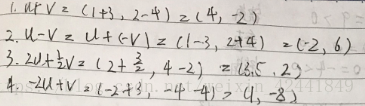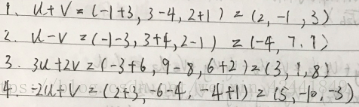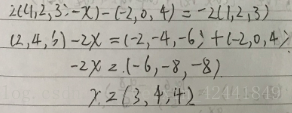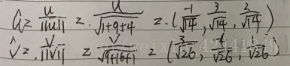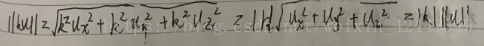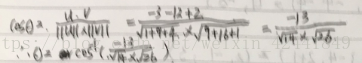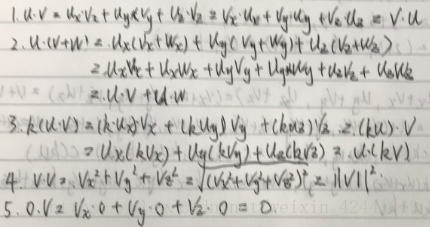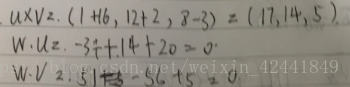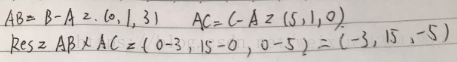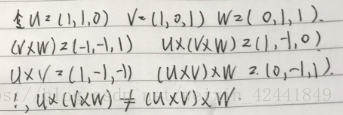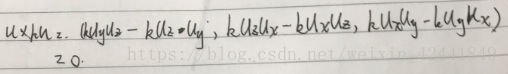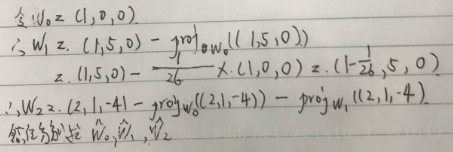Introduction to 3D Game Programming with DirectX 12 学习笔记之 --- 第一章：向量代数

原文:Introduction to 3D Game Programming with DirectX 12 学习笔记之 --- 第一章：向量代数

学习目标:

学习如何使用几何学和数字描述 Vector；
学习 Vector 的运算方法及其在几何学上的应用；
熟悉在 DirectXMath library 中的 Vector 相关的类和函数。

1 向量

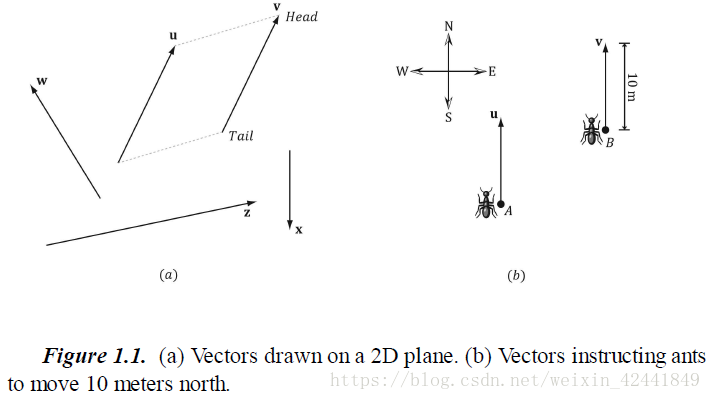
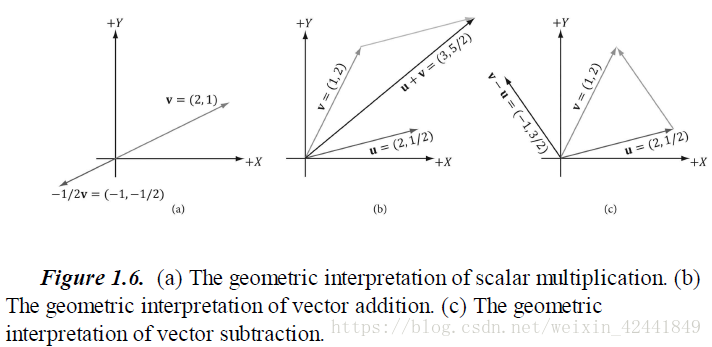
一个向量代表的是一个拥有大小和方向的量。类似力（拥有力的大小和方向）、位移（移动的方向和距离）、速度（速度的大小和方向）等，例如下图（图 1.1）：

绘制向量的位置和向量本身无关，所以当且仅当两个向量的大小和方形相等时，两个向量相等；所以上图中a和b中的向量u和向量v相等。

1.1 向量和坐标系统

我们现在可以定义各种向量几何运算来解决对应的问题，但是因为计算机无法直接通过几何学计算向量，所以我们需要用数字来描述向量；

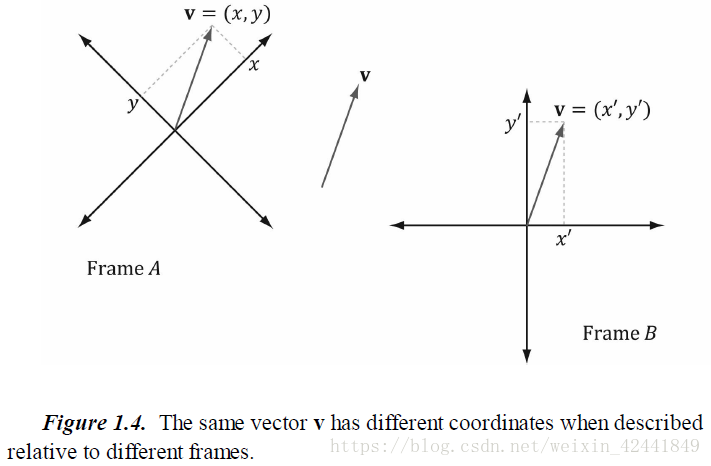
考虑到下图中的情况（图1.4），同一个向量在不同坐标系中会有不同的坐标变现：

在计算机3D图形学中我们需要使用多个坐标系，我们要知道当前在哪一个坐标系下，并且熟悉坐标系之间的转换。

1.2 左手坐标系 VS 右手坐标系

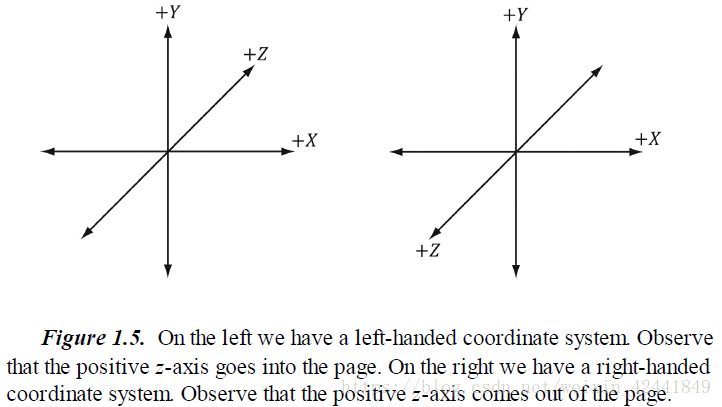
Direct3D 使用的是左手坐标系：如果你使用你的左手指向 X轴正方向，然后向Y轴正方向弯曲你的手指，此时你的大拇指指向的就是Z轴正方向，如图1.5 所示（右手坐标系类似，只不过替换为右手）

1.3 基本向量运算

我们也可以在坐标系中使用绘制的方法来表示：

2 长度和单位向量

向量长度计算公式：

单位向量计算公式：

为了证明单位向量计算公式，我们可以计算单位向量的长度：

3 向量的点积

向量的点积是一种结果为数量值的乘法形式，其定义和计算公式为：

向量的点积的定义并没有提出明显的几何定义，利用余弦定理，我们可以找到几何关系：

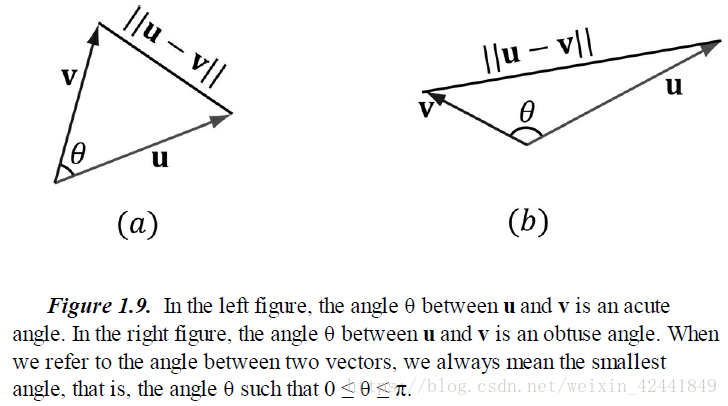
如图1.9，θ是向量v和u的夹角，再根据上面的公式，我们可以得出向量点积的一些有用的几何属性：

当两个向量点积为0时，两个向量垂直；
当两个向量点积大于0时，两个向量夹角小于90度；
当两个向量点积小于0时，两个向量夹角大于90度。

3.1 向量的分解

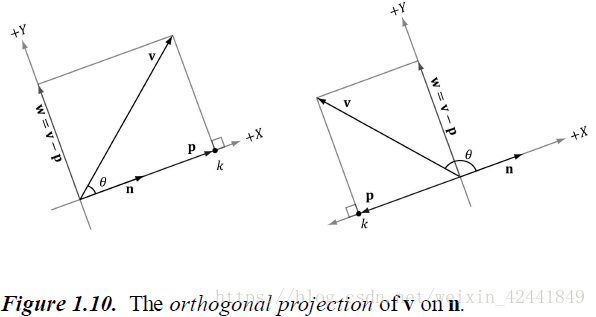
如图1.10

给出向量v和单位向量n，使用点积公式求出向量p：

向量p也可以表示为：p=projn(v)p = proj_n(v)p=projn(v)，那么向量w = v - p

所以向量v就可以分解为：v=p+w=projn(v)+perpn(v)v = p + w = proj_n(v) + perp_n(v)v=p+w=projn(v)+perpn(v)

如果向量n不是单位向量，那么可以提前把n标准化：

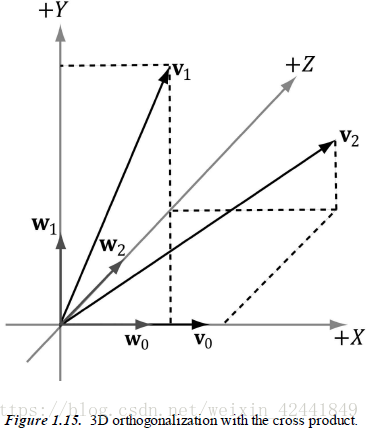
3.2 正交化

当一组向量相互之间都垂直，并且都是单位向量时，我们称他们为标准正交。在3D计算机图形学中，我们刚开始可能会有一组标准正交的向量，但是由于变量精度的问题，这些向量会在进行一系列计算后开始变得相互不垂直。所以我们的目标就是主要考虑在3D和2D情况下手动正交化。

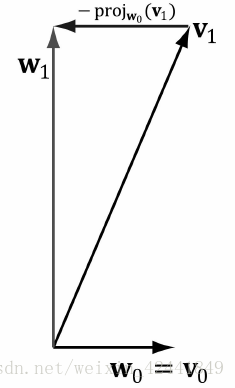
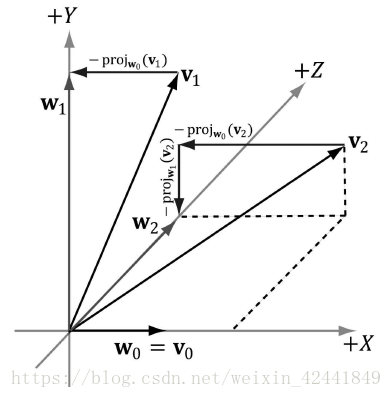
我们先从2D开始，假设拥有向量v0v_0v0和v1v_1v1，我们要将他们正交化为标准正交集w0w_0w0和w1w_1w1；首先我们使w0=v0w_0=v_0w0=v0，然后修改v1v_1v1让它垂直于w0w_0w0：

在3D情况下，我们继续然后修改v2v_2v2让它同时垂直于w0w_0w0和w1w_1w1：

最后一步是标准化每一个向量为单位向量。

这套正交化流程我们统一称之为 施密特正交化（Gram-Schmidt Orthogonalization）。

4 向量的叉积

两个向量的叉积（叉积不支持2D）结果为另外一个同时垂直于他俩的向量，叉积的运算公式为：

叉积不支持交换律，其交换后的结果是相反的，即：u * v = - v * u。

4.1 伪2D叉积

在2D情况下，如果已知u=(ux,uy)u = (u_x, u_y)u=(ux,uy)，找出垂直于u的向量v=(−uy,ux)v = (-u_y, u_x)v=(−uy,ux)，该公式的证明如下：

4.2 使用叉积正交化

使用叉积正交化会造成一些误差

首先设置 w0=v0∣∣v0∣∣w_0 = \frac{v_0}{||v_0||}w0=∣∣v0∣∣v0；
设置 w2=w0×v1∣∣w0×v1∣∣w_2 = \frac{w_0 \times v_1}{||w_0 \times v_1||}w2=∣∣w0×v1∣∣w0×v1；
最后 w1=w2×w0w_1 = w_2 \times w_0w1=w2×w0，因为w2w_2w2和w0w_0w0都已经是单位向量，所以不需要对w1w_1w1做标准化。

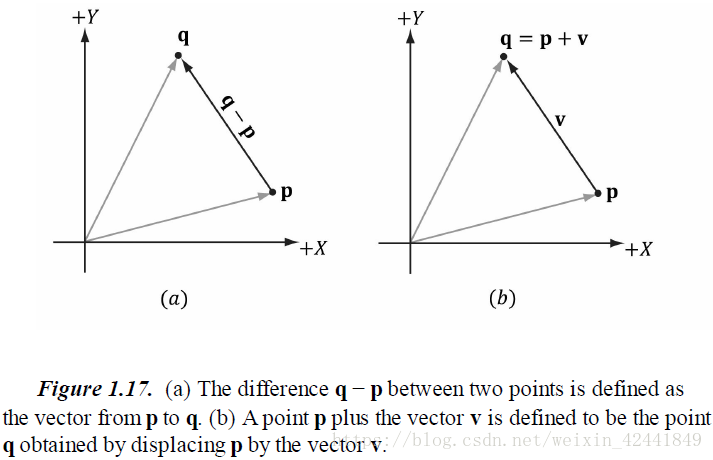
5 点

点在3D图形学中要来表示位置，在坐标系中，一个向量可以表示一个位置。

一方面，我们对向量的运算不能应用到点上（比如两个点相加是没有意义的）；另一方面，我们可以把这些运算扩展到点上。

6 DIRECTX MATH 中的向量

Direct Math是Direct3D应用中的一个数学库，并且已经内置到了Window 8以上的操作系统。

该数学库使用 SSE2(Streaming SIMD Extensions 2) 系统指令，支持128位的 SIMD(single instruction multiple data) 寄存器。SIMD 指令可以在一条指令中运算4个32位的浮点数和整数。这对于向量的计算非常有用。

比如做4D向量的相加，我们不需要使用4条标量相加指令，而是1条SIMD指令即可，对于2D和3D向量也可以使用SIMD，我们可以无视不使用的坐标系。

如果想要了解DirectX Math的全部细节，推荐阅读DirectX Math的在线文档；

如果想要知道SIMD向量库如何优化开发，或者了解它为何如此设计，推荐阅读文章：Designing Fast Cross-Platform SIMD Vector Libraries by [Oliveira2010]。

使用DirectX Math时，需要的所有头文件：

#include <DirectXMath.h>			// namespace: DirectX    			DirectX 数学库

#include <DirectXPackedVector.h>	// namespace: DirectX::PackedVector	一些额外附加数据类型

对于X86系统，需要开启SSE2(Project Properties > Configuration Properties > C/C++ > Code Generation > Enable Enhanced Instruction Set)；

对于所有系统，还需要开启快速浮点数模式**(Project Properties > Configuration Properties > C/C++ > Code Generation > Floating Point Model**)；

对于64位系统不需要开启SSE2，因为所有64位CPU都支持SSE2(http://en.wikipedia.org/wiki/SSE2)。

6.1 向量的类型

DirectX Math 的核心类型是映射到SIMD硬件寄存器的 XMVECTOR，它是一个128位，可以使用单个指令计算4个32位浮点数的类型。对于X86和64位系统中，它的定义如下：

typedef __m128 XMVECTOR;

__m128是SIMD专用的类型。当我们计算的时候，向量必须声明位该类型才能利用SIMD的优点。

XMVECTOR的局部和全部变量会自动被16位对其；对于类的成员变量，使用XMFLOAT2 (2D)，XMFLOAT3 (3D)，和XMFLOAT4 (4D) 来替换；

struct XMFLOAT2

{

	float x;

	float y;

	XMFLOAT2() {}

	XMFLOAT2(float _x, float _y) : x(_x), y(_y) {}

	explicit XMFLOAT2(_In_reads_(2) const float *pArray) : x(pArray[0]), y(pArray[1]) {}

	XMFLOAT2& operator= (const XMFLOAT2& Float2) { x = Float2.x; y = Float2.y; return *this; }

};

struct XMFLOAT3

{

	float x;

	float y;

	float z;

	XMFLOAT3() {}

	XMFLOAT3(float _x, float _y, float _z) : x(_x), y(_y), z(_z) {}

	explicit XMFLOAT3(_In_reads_(3) const float *pArray) : x(pArray[0]), y(pArray[1]), z(pArray[2]) {}

	XMFLOAT3& operator= (const XMFLOAT3& Float3) { x = Float3.x; y = Float3.y; z = Float3.z; return *this; }

};

struct XMFLOAT4

{

	float x;

	float y;

	float z;

	float w;

	XMFLOAT4() {}

	XMFLOAT4(float _x, float _y, float _z, float _w) : x(_x), y(_y), z(_z), w(_w) {}

	explicit XMFLOAT4(_In_reads_(4) const float *pArray) : x(pArray[0]), y(pArray[1]), z(pArray[2]), w(pArray[3]) {}

	XMFLOAT4& operator= (const XMFLOAT4& Float4) { x = Float4.x; y = Float4.y; z = Float4.z; w = Float4.w; return *this; }

};

如果直接利用这些类型进行计算，就无法利用SIMD的优点，所以我们需要进行类型的转换；DirectX Math中提供了Loading函数可以将XMFLOATn类型数据加载到XMVECTOR；Storage函数可以将XMVECTOR类型数据保存到XMFLOATn。

总结如下：

对于局部或者全局变量，使用XMVECTOR；
对于类的成员变量，使用XMFLOATn；
使用Loading和Storage函数对数据进行加载和保存；
计算的时候使用XMVECTOR类型；

6.2 Loading 和 Storage 方法

将数据从XMFLOATn加载到XMVECTOR的Loading方法如下：

// Loads XMFLOAT2 into XMVECTOR

XMVECTOR XM_CALLCONV XMLoadFloat2(const XMFLOAT2 *pSource);

// Loads XMFLOAT3 into XMVECTOR

XMVECTOR XM_CALLCONV XMLoadFloat3(const XMFLOAT3 *pSource);

// Loads XMFLOAT4 into XMVECTOR

XMVECTOR XM_CALLCONV XMLoadFloat4(const XMFLOAT4 *pSource);

将数据从XMVECTOR保存到XMFLOATn的Storage方法如下：

// Loads XMVECTOR into XMFLOAT2

void XM_CALLCONV XMStoreFloat2(XMFLOAT2 *pDestination, FXMVECTOR V);

// Loads XMVECTOR into XMFLOAT3

void XM_CALLCONV XMStoreFloat3(XMFLOAT3 *pDestination, FXMVECTOR V);

// Loads XMVECTOR into XMFLOAT4

void XM_CALLCONV XMStoreFloat4(XMFLOAT4 *pDestination, FXMVECTOR V);

有时我们只想修改或者获取XMVECTOR中的某一个值，可以使用下面的函数很容易实现：

float XM_CALLCONV XMVectorGetX(FXMVECTOR V);

float XM_CALLCONV XMVectorGetY(FXMVECTOR V);

float XM_CALLCONV XMVectorGetZ(FXMVECTOR V);

float XM_CALLCONV XMVectorGetW(FXMVECTOR V);

XMVECTOR XM_CALLCONV XMVectorSetX(FXMVECTOR V, float x);

XMVECTOR XM_CALLCONV XMVectorSetY(FXMVECTOR V, float y);

XMVECTOR XM_CALLCONV XMVectorSetZ(FXMVECTOR V, float z);

XMVECTOR XM_CALLCONV XMVectorSetW(FXMVECTOR V, float w);

6.3 参数传递

为了优化性能为目的，XMVECTOR可以作为函数参数直接传递到SSE/SSE2寄存器中（而不是堆栈内存），参数传递的数量依赖于平台（例如：32/64位 Windows，Windows RT）和编译器。所以根据不同平台/编译器，我们使用FXMVECTOR，GXMVECTOR，HXMVECTOR 和 CXMVECTOR类型来传递XMVECTOR参数；此外，在函数名前要指明调用注释XM_CALLCONV

XMVECTOR类型参数传递规则如下：

前三个参数类型要定义为FXMVECTOR；
第四个要定义为GXMVECTOR；
第五个和第六个要定义为HXMVECTOR；
其他参数要定义为CXMVECTOR。

在32为Windows下，支持__fastcall调用约定和支持更新的__vectorcall调用约定编译中，参数定义如下：

// 32-bit Windows __fastcall passes first 3 XMVECTOR arguments

// via registers, the remaining on the stack.

typedef const XMVECTOR FXMVECTOR;

typedef const XMVECTOR& GXMVECTOR;

typedef const XMVECTOR& HXMVECTOR;

typedef const XMVECTOR& CXMVECTOR;

// 32-bit Windows __vectorcall passes first 6 XMVECTOR arguments

// via registers, the remaining on the stack.

typedef const XMVECTOR FXMVECTOR;

typedef const XMVECTOR GXMVECTOR;

typedef const XMVECTOR HXMVECTOR;

typedef const XMVECTOR& CXMVECTOR;

想了解在其他平台定义的更多细节，可以阅读DirectX Math的文档，“Library Internals” 下的 “Calling Conventions” ；

在构造函数中，这些规则是例外：文档推荐前三个参数使用FXMVECTOR，其他参数使用CXMVECTOR，并且不要为构造函数添加XM_CALLCONV；

inline XMMATRIX XM_CALLCONV XMMatrixTransformation(

	FXMVECTOR ScalingOrigin,

	FXMVECTOR ScalingOrientationQuaternion, .

	FXMVECTOR Scaling,

	GXMVECTOR RotationOrigin,

	HXMVECTOR RotationQuaternion,

	HXMVECTOR Translation);

函数调用时也可以添加非XMVECTOR类型参数，XMVECTOR参数定义规则相同，非XMVECTOR类型参数不计数：

inline XMMATRIX XM_CALLCONV XMMatrixTransformation2D(

	FXMVECTOR ScalingOrigin,

	float ScalingOrientation,

	FXMVECTOR Scaling,

	FXMVECTOR RotationOrigin,

	float Rotation,

	GXMVECTOR Translation);

这些规则只使用于输入参数，输出参数不使用SSE/SSE2寄存器，所以会被对待为和非XMVECTOR类型参数一样。

6.4 常量向量

常量向量的实例需要使用XMVECTORF32类型，下面是一些在DirectX SDK里CascadedShadowMaps11 Demo 下的例子：

static const XMVECTORF32 g_vHalfVector = { 0.5f, 0.5f, 0.5f, 0.5f };

static const XMVECTORF32 g_vZero = { 0.0f, 0.0f, 0.0f, 0.0f };

XMVECTORF32 vRightTop = {

	vViewFrust.RightSlope,

	vViewFrust.TopSlope,

	1.0f,1.0f

	};

XMVECTORF32 vLeftBottom = {

	vViewFrust.LeftSlope,

	vViewFrust.BottomSlope,

	1.0f,1.0f

	};

其实所有类似的初始化操作都可以使用XMVECTORF32类型，它是一个16位对齐并带有XMVECTOR转换的结构体，它的定义如下：

// Conversion types for constants

__declspec(align(16)) struct XMVECTORF32

{

	union

	{

		float f[4];

		XMVECTOR v;

	};

	inline operator XMVECTOR() const { return v; }

	inline operator const float*() const { return f; }

	#if !defined(_XM_NO_INTRINSICS_) &&

		defined(_XM_SSE_INTRINSICS_)

		inline operator __m128i() const { return _mm_castps_si128(v); }

		inline operator __m128d() const { return _mm_castps_pd(v); }

	#endif

};

你也可以使用XMVECTORU32创建XMVECTOR整形常量：

static const XMVECTORU32 vGrabY = { 0x00000000,0xFFFFFFFF,0x00000000,0x00000000 };

6.5 重载运算符

XMVECTOR有几个重载运算符来计算向量的加减和量乘法：

XMVECTOR XM_CALLCONV operator+ (FXMVECTOR V);

XMVECTOR XM_CALLCONV operator- (FXMVECTOR V);

XMVECTOR& XM_CALLCONV operator+= (XMVECTOR& V1, FXMVECTOR V2);

XMVECTOR& XM_CALLCONV operator-= (XMVECTOR& V1, FXMVECTOR V2);

XMVECTOR& XM_CALLCONV operator*= (XMVECTOR& V1, FXMVECTOR V2);

XMVECTOR& XM_CALLCONV operator/= (XMVECTOR& V1, FXMVECTOR V2);

XMVECTOR& operator*= (XMVECTOR& V, float S);

XMVECTOR& operator/= (XMVECTOR& V, float S);

XMVECTOR XM_CALLCONV operator+ (FXMVECTOR V1, FXMVECTOR V2);

XMVECTOR XM_CALLCONV operator- (FXMVECTOR V1, FXMVECTOR V2);

XMVECTOR XM_CALLCONV operator* (FXMVECTOR V1, FXMVECTOR V2);

XMVECTOR XM_CALLCONV operator/ (FXMVECTOR V1, FXMVECTOR V2);

XMVECTOR XM_CALLCONV operator* (FXMVECTOR V, float S);

XMVECTOR XM_CALLCONV operator* (float S, FXMVECTOR V);

XMVECTOR XM_CALLCONV operator/ (FXMVECTOR V, float S);

6.6 其它

DirectX Math定义了一些有用的常量来近似的表现和 π 相关的值：

const float XM_PI = 3.141592654f;

const float XM_2PI = 6.283185307f;

const float XM_1DIVPI = 0.318309886f;

const float XM_1DIV2PI = 0.159154943f;

const float XM_PIDIV2 = 1.570796327f;

const float XM_PIDIV4 = 0.785398163f;

另外，还定义了下面的内敛函数用以在转换角度和弧度：

inline float XMConvertToRadians(float fDegrees) { return fDegrees * (XM_PI / 180.0f); }

inline float XMConvertToDegrees(float fRadians) { return fRadians * (180.0f / XM_PI); }

还定义了min/max函数：

template<class T> inline T XMMin(T a, T b) { return (a < b) ? a : b; }

template<class T> inline T XMMax(T a, T b) { return (a > b) ? a : b; }

6.7 Setter 函数

DirectX Math提供了下面函数用来修改XMVECTOR的值：

// Returns the zero vector 0

XMVECTOR XM_CALLCONV XMVectorZero();

// Returns the vector (1, 1, 1, 1)

XMVECTOR XM_CALLCONV XMVectorSplatOne();

// Returns the vector (x, y, z, w)

XMVECTOR XM_CALLCONV XMVectorSet(float x, float y, float z, float w);

// Returns the vector (s, s, s, s)

XMVECTOR XM_CALLCONV XMVectorReplicate(float Value);

// Returns the vector (vx, vx, vx, vx)

XMVECTOR XM_CALLCONV XMVectorSplatX(FXMVECTOR V);

// Returns the vector (vy, vy, vy, vy)

XMVECTOR XM_CALLCONV XMVectorSplatY(FXMVECTOR V);

// Returns the vector (vz, vz, vz, vz)

XMVECTOR XM_CALLCONV XMVectorSplatZ(FXMVECTOR V);

下面的代码解释了大部分函数的使用：

#include <windows.h> // for XMVerifyCPUSupport

#include <DirectXMath.h>

#include <DirectXPackedVector.h>

using namespace std;

using namespace DirectX;

using namespace DirectX::PackedVector;

// Overload the "<<" operators so that we can use cout to

// output XMVECTOR objects.

ostream& XM_CALLCONV operator<<(ostream& os, FXMVECTOR v)

{

	XMFLOAT3 dest;

	XMStoreFloat3(&dest, v);

	os << "(" << dest.x << ", " << dest.y << ", "

	<< dest.z << ")";

	return os;

} 

int main()

{

	cout.setf(ios_base::boolalpha);

	// Check support for SSE2 (Pentium4, AMD K8, and above).

	if (!XMVerifyCPUSupport())

	{

		cout << "directx math not supported" << endl;

		return 0;

	}

	XMVECTOR p = XMVectorZero();

	XMVECTOR q = XMVectorSplatOne();

	XMVECTOR u = XMVectorSet(1.0f, 2.0f, 3.0f, 0.0f);

	XMVECTOR v = XMVectorReplicate(-2.0f);

	XMVECTOR w = XMVectorSplatZ(u);

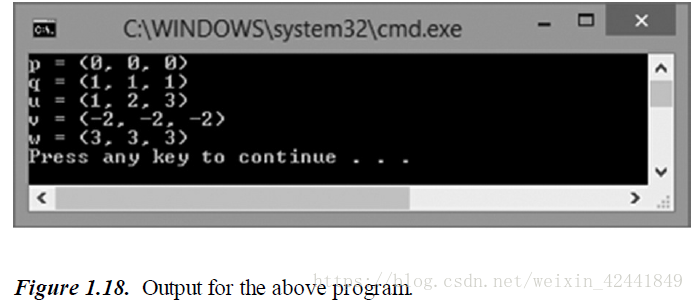
	cout << "p = " << p << endl;

	cout << "q = " << q << endl;

	cout << "u = " << u << endl;

	cout << "v = " << v << endl;

	cout << "w = " << w << endl;

	return 0;

}

6.8 向量的函数

DirectX Math提供了下面的函数来处理各种向量运算，这里介绍3D版本，2D和4D版本于3D类似：

（有些可以直接返回值的函数依然返回的是XMVECTOR，比如向量的点积，这样做是为了尽可能减少SIMD和其它值的混合，从而提高性能）

XMVECTOR XM_CALLCONV XMVector3Length(

	// Returns ||v||

	FXMVECTOR V); // Input v

XMVECTOR XM_CALLCONV XMVector3LengthSq(

	// Returns ||v||2

	FXMVECTOR V); // Input v

XMVECTOR XM_CALLCONV XMVector3Dot(

	// Returns v1·v2

	FXMVECTOR V1, // Input v1

	FXMVECTOR V2); // Input v2

XMVECTOR XM_CALLCONV XMVector3Cross(

	// Returns v1 × v2

	FXMVECTOR V1, // Input v1

	FXMVECTOR V2); // Input v2

XMVECTOR XM_CALLCONV XMVector3Normalize(

	// Returns v/||v||

	FXMVECTOR V); // Input v

XMVECTOR XM_CALLCONV XMVector3Orthogonal(

	// Returns a vector orthogonal to v

	FXMVECTOR V); // Input v

XMVECTOR XM_CALLCONV XMVector3AngleBetweenVectors(

	// Returns the angle between v1 and v2

	FXMVECTOR V1, // Input v1

	FXMVECTOR V2); // Input v2

void XM_CALLCONV XMVector3ComponentsFromNormal(

	XMVECTOR* pParallel, // Returns projn(v)

	XMVECTOR* pPerpendicular, // Returns perpn(v)

	FXMVECTOR V, // Input v

	FXMVECTOR Normal); // Input n

bool XM_CALLCONV XMVector3Equal(

	// Returns v1 = v2

	FXMVECTOR V1, // Input v1

	FXMVECTOR V2); // Input v2

bool XM_CALLCONV XMVector3NotEqual(

	// Returns v1 ≠ v2

	FXMVECTOR V1, // Input v1

	FXMVECTOR V2); // Input v2

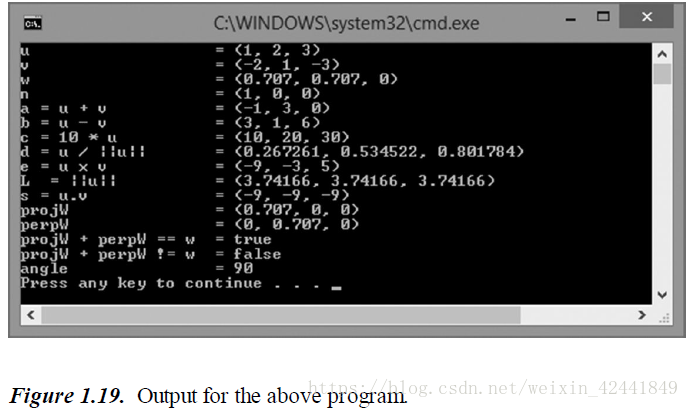
下面的示例程序展示了大部分函数和一些重载云算符的用法：

#include <windows.h> // for XMVerifyCPUSupport

#include <DirectXMath.h>

#include <DirectXPackedVector.h>

#include <iostream>

using namespace std;

using namespace DirectX;

using namespace DirectX::PackedVector;

// Overload the "<<" operators so that we can use cout to

// output XMVECTOR objects.

ostream& XM_CALLCONV operator<<(ostream& os, FXMVECTOR v)

{

	XMFLOAT3 dest;

	XMStoreFloat3(&dest, v);

	os << "(" << dest.x << ", " << dest.y << ", "

	<< dest.z << ")";

	return os;

}

int main()

{

	cout.setf(ios_base::boolalpha);

	// Check support for SSE2 (Pentium4, AMD K8, and above).

	if (!XMVerifyCPUSupport())

	{

		cout << "directx math not supported" << endl;

		return 0;

	}

	XMVECTOR n = XMVectorSet(1.0f, 0.0f, 0.0f, 0.0f);

	XMVECTOR u = XMVectorSet(1.0f, 2.0f, 3.0f, 0.0f);

	XMVECTOR v = XMVectorSet(-2.0f, 1.0f, -3.0f, 0.0f);

	XMVECTOR w = XMVectorSet(0.707f, 0.707f, 0.0f, 0.0f);

	// Vector addition: XMVECTOR operator +

	XMVECTOR a = u + v;

	// Vector subtraction: XMVECTOR operator -

	XMVECTOR b = u - v;

	// Scalar multiplication: XMVECTOR operator *

	XMVECTOR c = 10.0f*u;

	// ||u||

	XMVECTOR L = XMVector3Length(u);

	// d = u / ||u||

	XMVECTOR d = XMVector3Normalize(u);

	// s = u dot v

	XMVECTOR s = XMVector3Dot(u, v);

	// e = u x v

	XMVECTOR e = XMVector3Cross(u, v);

	// Find proj_n(w) and perp_n(w)

	XMVECTOR projW;

	XMVECTOR perpW;

	XMVector3ComponentsFromNormal(&projW, &perpW, w, n);

	// Does projW + perpW == w?

	bool equal = XMVector3Equal(projW + perpW, w) != 0;

	bool notEqual = XMVector3NotEqual(projW + perpW, w) != 0;

	// The angle between projW and perpW should be 90 degrees.

	XMVECTOR angleVec = XMVector3AngleBetweenVectors(projW, perpW);

	float angleRadians = XMVectorGetX(angleVec);

	float angleDegrees = XMConvertToDegrees(angleRadians);

	cout << "u = " << u << endl;

	cout << "v = " << v << endl;

	cout << "w = " << w << endl;

	cout << "n = " << n << endl;

	cout << "a = u + v = " << a << endl;

	cout << "b = u - v = " << b << endl;

	cout << "c = 10 * u = " << c << endl;

	cout << "d = u / ||u|| = " << d << endl;

	cout << "e = u x v = " << e << endl;

	cout << "L = ||u|| = " << L << endl;

	cout << "s = u.v = " << s << endl;

	cout << "projW = " << projW << endl;

	cout << "perpW = " << perpW << endl;

	cout << "projW + perpW == w = " << equal << endl;

	cout << "projW + perpW != w = " << notEqual << endl;

	cout << "angle = " << angleDegrees << endl;

	return 0;

}

DirectX Math还包含一些求近似值的函数，它们准确度较低，但是更快；如果你愿意牺牲准确度去追求速度，可以考虑使用它们，下面是其中的2个例子：

XMVECTOR XM_CALLCONV XMVector3LengthEst(

	// Returns estimated ||v||

	FXMVECTOR V); // Input v

XMVECTOR XM_CALLCONV XMVector3NormalizeEst(

	// Returns estimated v/||v||

	FXMVECTOR V); // Input v

6.9 浮点数误差

DirectX Math库提供了一个函数XMVector3NearEqual用以判断两个向量在可允许的误差下是否相等：

// Returns

// abs(U.x – V.x) <= Epsilon.x &&

// abs(U.y – V.y) <= Epsilon.y &&

// abs(U.z – V.z) <= Epsilon.z

XMFINLINE bool XM_CALLCONV XMVector3NearEqual(

	FXMVECTOR U,

	FXMVECTOR V,

	FXMVECTOR Epsilon);

7 总结

向量用来模拟在物理学中同时具有方向和长度的量；在几何学上，我们使用一个具有方向的线段来表示向量。当一个向量平行移动到使其尾部和坐标系原点重合的时候，它就是一个标准向量，标准向量可以使用它头部坐标来表示；
向量的基本运算公式：
当进行向量运算的时候，我们使用XMVECTOR类型来进行高效的SIMD操作；对于类的成员变量，我们使用XMFLOAT2，XMFLOAT3，和XMFLOAT4类型；然后使用Loading和Storage方法来进行它们之间的转化；
出于对效率考虑，XMVECTOR类型的数据可以作为函数参数直接传到SSE/SSE2寄存器中，为了独立于平台，我们使用FXMVECTOR，GXMVECTOR，HXMVECTOR 和 CXMVECTOR类型来传递XMVECTOR参数。传递的规则为：前三个参数使用FXMVECTOR类型，第四个参数使用GXMVECTOR类型，第五个和第六个参数使用HXMVECTOR类型，其它的使用CXMVECTOR类型；
XMVECTOR类重载了算术运算符来计算加减和标量乘法；DirectX Math库还提供了很多有用的函数来计算向量的长度，向量长度的平方，向量的点积和叉积，向量标准化：

XMVECTOR XM_CALLCONV XMVector3Length(FXMVECTOR V);

XMVECTOR XM_CALLCONV XMVector3LengthSq(FXMVECTOR V);

XMVECTOR XM_CALLCONV XMVector3Dot(FXMVECTOR V1, FXMVECTOR V2);

XMVECTOR XM_CALLCONV XMVector3Cross(FXMVECTOR V1, FXMVECTOR V2);

XMVECTOR XM_CALLCONV XMVector3Normalize(FXMVECTOR V);

8 练习题

令u = (1, 2)、v = (3, −4)，计算下面的值：
令u = (−1, 3, 2)、v = (3, −4, 1)，计算下面的值：
假设u = (ux, uy, uz)，v = (vx, vy, vz)和w = (wx, wy, wz)。并且c和k是标量，证明下面的等式：
解方程2((1, 2, 3) – x) − (−2, 0, 4) = −2(1, 2, 3)：
令u = (−1, 3, 2)、v = (3, −4, 1)，标准化u和v：
令k是一个标量，u = (ux, uy, uz)，证明||ku|| = |k|||u||：
求u和v的夹角是垂直、锐角还是钝角：
令u = (−1, 3, 2)和v = (3, −4, 1)，求u和v的夹角：
令u = (ux, uy, uz)、v = (vx, vy, vz)和w = (wx, wy, wz)，c和是标量，证明下面等式：
利用余弦法则（c2c^2c2 = a2a^2a2 + b2b^2b2 – 2abcosθ）证明uxvx+uyvy+uzvz=∣∣u∣∣∣∣v∣∣cosθu_xv_x + u_yv_y + u_zv_z = ||u||||v|| cosθuxvx+uyvy+uzvz=∣∣u∣∣∣∣v∣∣cosθ：
令n = (−2, 1)，将g = (0, −9.8)分解为2个向量，其中一个平行于n，另一个垂直于n：
令u = (−2, 1, 4)、v = (3, −4, 1)，求w = u × v，并且证明w · u = 0和w · v = 0：
3个点A = (0, 0, 0)，B = (0, 1, 3)和C = (5, 1, 0)在某坐标系中定义了一个三角形，找到一个垂直于该三角形的向量：
证明∣∣∣u×v∣∣=∣∣u∣∣∣∣v∣∣sinθ|||u\times v|| = ||u||||v||sinθ∣∣∣u×v∣∣=∣∣u∣∣∣∣v∣∣sinθ：

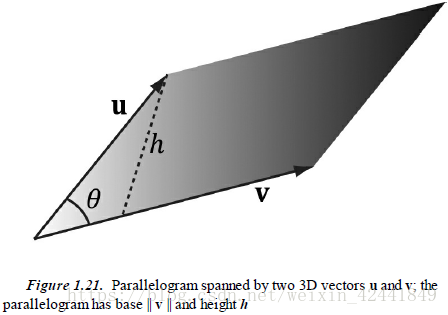
这个没有想到太好的办法，就是把sinθ转化为1−cos2θ\sqrt{1-cos^2θ}1−cos2θ，然后全部展开为uvxyzuv_{xyz}uvxyz，因为这种暴力破解法展开后等式会变得非常长，我懒得展了，看起来是一样哈哈。
证明||u ×v||的值是由u和v组成的平行四边形的面积：
给出一组3D向量u,v和w，证明u×(v×w)!=(u×v)×wu \times (v \times w) != (u \times v) \times wu×(v×w)!=(u×v)×w，这个代表了叉积不符合组合率：
证明两个非0平行向量的叉积是0：u × ku = 0。
使用施密特正交化方法，标准正交化下列向量：{(1, 0, 0), (1, 5, 0), (2, 1, −4)}
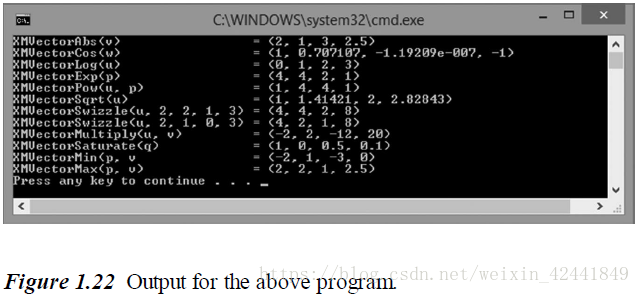
根据下列代码的输出，猜测每个XMVector*函数的作用，然后查阅DirectXMath的文档：

https://docs.microsoft.com/zh-cn/windows/desktop/dxmath/ovw-xnamath-reference-functions-vector

#include <windows.h> // for XMVerifyCPUSupport

#include <DirectXMath.h>

#include <DirectXPackedVector.h>

#include <iostream>

using namespace std;

using namespace DirectX;

using namespace DirectX::PackedVector;

// Overload the "<<" operators so that we can use cout to

// output XMVECTOR objects.

ostream& XM_CALLCONV operator<<(ostream& os, FXMVECTOR v)

{

	XMFLOAT4 dest;

	XMStoreFloat4(&dest, v);

	os << "(" << dest.x << ", " << dest.y << ", " << dest.z << ", " << dest.w << ")";

	return os;

}

int main()

{

	cout.setf(ios_base::boolalpha);

	// Check support for SSE2 (Pentium4, AMD K8, and above).

	if (!XMVerifyCPUSupport())

	{

		cout << "directx math not supported" << endl;

		return 0;

	}

	XMVECTOR p = XMVectorSet(2.0f, 2.0f, 1.0f, 0.0f);

	XMVECTOR q = XMVectorSet(2.0f, -0.5f, 0.5f, 0.1f);

	XMVECTOR u = XMVectorSet(1.0f, 2.0f, 4.0f, 8.0f);

	XMVECTOR v = XMVectorSet(-2.0f, 1.0f, -3.0f, 2.5f);

	XMVECTOR w = XMVectorSet(0.0f, XM_PIDIV4, XM_PIDIV2, XM_PI);

	cout << "XMVectorAbs(v) = " << XMVectorAbs(v) << endl;			// 对每一个分量求绝对值

	cout << "XMVectorCos(w) = " << XMVectorCos(w) << endl;			// 对每一个分量求arccosine值

	cout << "XMVectorLog(u) = " << XMVectorLog(u) << endl;			// 对每一个分量求log2的值

	cout << "XMVectorExp(p) = " << XMVectorExp(p) << endl;			// 对每一个分量乘2的值

	cout << "XMVectorPow(u, p) = " << XMVectorPow(u, p) << endl;	// 对u的每一个分量做p对应分量的平方

	cout << "XMVectorSqrt(u) = " << XMVectorSqrt(u) << endl;		// 对每一个分量开平方

	cout << "XMVectorSwizzle(u, 2, 2, 1, 3) = " << XMVectorSwizzle(u, 2, 2, 1, 3) << endl;	// XMVectorSwizzle 没看懂 - -！

	cout << "XMVectorSwizzle(u, 2, 1, 0, 3) = " << XMVectorSwizzle(u, 2, 1, 0, 3) << endl;	// XMVectorSwizzle 没看懂 - -！

	cout << "XMVectorMultiply(u, v) = " << XMVectorMultiply(u, v) << endl;	// 对每一个对应分量相乘

	cout << "XMVectorSaturate(q) = " << XMVectorSaturate(q) << endl;	// 把每一个分量修改为0~1的值

	cout << "XMVectorMin(p, v = " << XMVectorMin(p, v) << endl;			// 对每一个分量求 最小/最大 的值

	cout << "XMVectorMax(p, v) = " << XMVectorMax(p, v) << endl;		// 对每一个分量求 最小/最大 的值

	system("pause");

	return 0;

}