【期望dp 质因数分解】cf1139D. Steps to One

有一种组合方向的考虑有没有dalao肯高抬啊？

题目大意

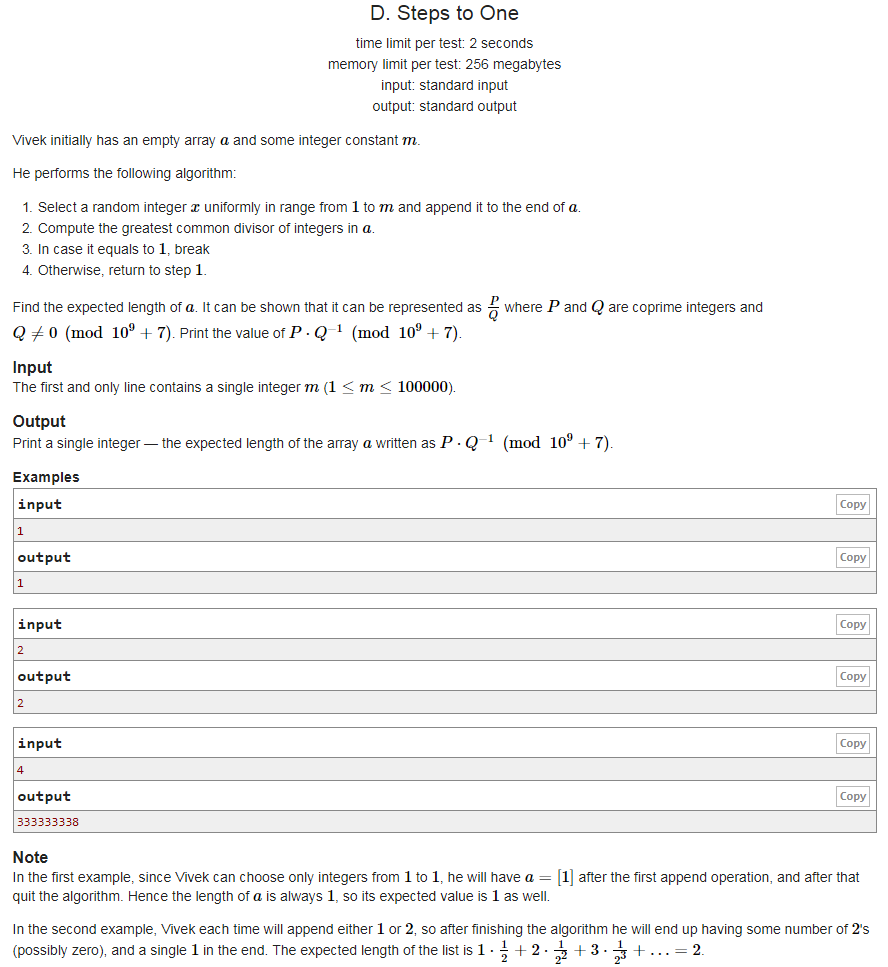
有一个初始为空的数组$a$，按照以下的流程进行操作：

• 在$1\cdots m$中等概率选出一个数$x$并添加到$a$的末尾
• 如果$a$中所有元素的$\gcd=1$则完成这个数组$a$的修改
• 重复这一过程

求数组$a$的期望长度，$m \le 10^5,\mod 10^9+7$

---

题目分析

质因数分解的期望dp题

以下介绍的两个做法中，第一个做法本人不会所以  求助会做的dalao麻烦高抬一手   ；

第二个做法是对推得的dp式子质因数分解求解————当然网上更多的是莫比乌斯反演的做法，此处就不介绍了。

未完的做法一：组合考虑

考虑计算$f(d)$为：数组$a$的前$len-1$个（也即结束前的那一序列）$\gcd=d$时，对答案的期望长度贡献。

那么枚举结束前的长度$i$，记$h(d)$为$1\cdots m$中与$d$互质的数的个数；$g(i,d)$为一个$\gcd=d$的长度为$i$的序列的概率，有$f(d)=\sum\limits_{i=1}^{∞}(i+1)\times g(i,d)\times h(d)$。

当然，这样的式子远远不够。$h(d)$的计算非常轻松但是问题在于$g(i,d)$有没有什么组合上的表达方式。我最初以为$g(i,d)=\lfloor\frac{m}{d}\rfloor^{i-1}\times \frac{1}{m}$，意即将序列看做是无序取入的集合，确保$i-1$个元素都是$\{d,2d,3d\cdots\}$，并钦点一个$d$.但是这个处理有两个问题：1.序列不能够这样看成无序集合；2.并不是必须要有一个$d$才能使数组的$\gcd=d$，例如$\{2d,3d,5d\}$就有$\gcd=d$。

这个方向大概不太能行吧，为求出式子，$g(i,d)$可能还有更严苛的表达限制。

做法二：质因数分解

由于这里的长度是无穷的，所以处理角度还当是从序列的$\gcd$入手。

记$f_d$为当前数组已经$\gcd=d$，到达$\gcd=1$的状态的期望步数。（这个状态要比我上面那个状态要优秀得多）

容易得到转移　　$f_d=1+\frac{1}{m} \sum\limits_{i=1}^mf_{\gcd(i,d)}$，

稍作化简得到　　$f_d=1+\frac{1}{m} \sum\limits_{i\mid d,i\ne d}(f_i\times c(i,d)+\lfloor\frac{m}{d}\rfloor f_d)$，其中$c(i,d)=\sum\limits_{j=1}^m[\gcd (d,j)=i]$.

通过移项，有　　$f_d=\frac{1+\frac{1}{m} \sum\limits_{i\mid d,i\ne d}f_i\times c(i,d)}{1-\frac{1}{m}\lfloor\frac{m}{d}\rfloor}$

那么对于这里$c(i,d)$的处理，就有很多方法了。这里介绍质因数分解的做法：

由于　　$c(i,d)=\sum\limits_{j=1}^m[\gcd (d,j)=i]=\sum\limits_{j=1}^{\lfloor \frac{m}{i} \rfloor}[\gcd (\lfloor\frac{d}{i}\rfloor,j)=1]$，考虑子问题：$1\cdots c$中与$q$互质的数的个数。

那么将$q$唯一分解，有$q=p_1^{k_1}p_2^{k_2}\cdots$。注意到实际上我们只关心$p_i$而不关心$k_i$，所求的也就是$1\cdots c$中不存在任何$p_i$因数的数的个数。至此转为一个经典容斥问题，可以预处理出$r$个素因数再$2^r$容斥解决。

接下来是一些题外话，

上面提到的分解素因数的过程，理论上由于$10^5$内的数最多只有$6$个素因数，那么枚举每个素数检查是否为其因数的方法看上去也不算太差，

然而获得了1700ms+的“好”成绩：

一开始我还以为是$2^r$的dfs飞天了，然而后来意识到上述的这个素数分解的方法常数的确是巨大的……

可以这么看：对于一个要处理的数$x$，共约要遍历$\frac{x}{\ln x}$个素数。那么在这一部分上的总期望时间花费就大致是$\frac{m^2\sqrt m}{\ln m}$（好像这个上界太松没什么价值？）。

总之判断约数是否为质数的方法就要快很多：

 #include<bits/stdc++.h>
 #define MO 1000000007
 typedef long long ll;
 typedef std::vector<int> vec;
 const int maxn = ;

 int n,num,cnt,pr[maxn],phi[maxn];
 bool vis[maxn];
 ll ans,f[maxn];
 vec fac[maxn],opt;

 void makePrime()
 {
     phi[] = ;
     for (int i=; i<maxn; i++)
     {
         if (!vis[i]) pr[++pr[]] = i, phi[i] = i-;
         for (int j=,chk=; j<=pr[]&&i*pr[j]<maxn&&chk; j++)
             if (pr[j]%i) phi[i*pr[j]] = phi[i]*(pr[j]-);
             else chk = , phi[i*pr[j]] = phi[i]*pr[j];
     }
     for (int i=; i<maxn; i++)
         for (int j=i; j<maxn; j+=i) fac[j].push_back(i);
 }
 int qmi(int a, int b)
 {
     int ret = ;
     for (; b; b>>=,a=1ll*a*a%MO)
         if (b&) ret = 1ll*ret*a%MO;
     return ret;
 }
 void dfs(int x, int c, int t)
 {
     if (x==opt.size()) cnt += ((t&)?-num/c:num/c);
     else{
         dfs(x+, c, t);
         dfs(x+, c*opt[x], t+);
     }
 } int calc(int p, int d)
 {
     vec().swap(opt), p /= d, num = n/d;
     for (int pri; p>; )
     {
         pri = fac[p][];
         if (vis[pri]) break;
         opt.push_back(pri);
         while (p%pri==) p /= pri;
     }
     cnt = , dfs(, , );
     return cnt;
 }
 int main()
 {
     scanf("%d",&n), ans = , f[] = ;
     makePrime();
     for (int i=; i<=n; i++)
     {
         int lwr = (-1ll*qmi(n, MO-)*(n/i)%MO+MO)%MO;
         for (int j=; j<fac[i].size()-; j++)
             f[i] = (f[i]+1ll*f[fac[i][j]]*calc(i, fac[i][j])%MO)%MO;
         f[i] = 1ll*(1ll*f[i]*qmi(n, MO-)%MO+)*qmi(lwr, MO-)%MO;
         ans = (ans+f[i]+)%MO;
     }
     printf("%lld\n",1ll*ans*qmi(n, MO-)%MO);
     return ;
 }

END