广度优先搜索（BFS）

广度优先搜索算法（Breadth-First-Search），又译作宽度优先搜索，或横向优先搜索，简称BFS，是一种图形搜索算法。简单的说，BFS是从根节点开始，沿着树的宽度遍历树的节点。如果所有节点均被访问，则算法中止。

原理：从算法的观点，所有因为展开节点而得到的子节点都会被加进一个先进先出的队列中。

实现方法：

1. 首先将根节点放入队列中。
2. 从队列中取出第一个节点，并检验它是否为目标。
   • 如果找到目标，则结束搜寻并回传结果。
   • 否则将它所有尚未检验过的直接子节点加入队列中。
3. 若队列为空，表示整张图都检查过了——亦即图中没有欲搜寻的目标。结束搜寻并回传“找不到目标”。
4. 重复步骤2。

特性

空间复杂度

因为所有节点都必须被储存，因此BFS的空间复杂度为 O(|V| + |E|)，其中 |V| 是节点的数目，而 |E| 是图中边的数目。注：另一种说法称BFS的空间复杂度为
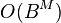，其中 B 是最大分支系数，而 M 是树的最长路径长度。由于对空间的大量需求，因此BFS并不适合解非常大的问题。

时间复杂度

最差情形下，BFS必须寻找所有到可能节点的所有路径，因此其时间复杂度为 O(|V| + |E|)，其中 |V| 是节点的数目，而 |E| 是图中边的数目。

完全性

广度优先搜索算法具有完全性。这意指无论图形的种类如何，只要目标存在，则BFS一定会找到。然而，若目标不存在，且图为无限大，则BFS将不收敛（不会结束）。

最佳解

若所有边的长度相等，广度优先搜索算法是最佳解——亦即它找到的第一个解，距离根节点的边数目一定最少；但对一般的图来说，BFS并不一定回传最佳解。这是因为当图形为加权图（亦即各边长度不同）时，BFS仍然回传从根节点开始，经过边数目最少的解；而这个解距离根节点的距离不一定最短。这个问题可以使用考虑各边权值，BFS的改良算法成本一致搜寻法来解决。然而，若非加权图形，则所有边的长度相等，BFS就能找到最近的最佳解。

java实现：

package Map;

import java.util.LinkedList;
import java.util.Queue;

public class BFS {
	static int m = Integer.MAX_VALUE;
	static Queue<Integer> q=new LinkedList<Integer>();
	static int[] visited=new int[7];
	static int[][]  map = { {0, 0, 0, 0, 0, 0, 0},
							{0, m, 6, 1, 5, m, m},
							{0, 6, m, 5, m, 3, m},
							{0, 1, 5, m, 5, 6, 4},
							{0, 5, m, 5, m, m, 2},
							{0, m, 3, 6, m, m, 6},
							{0, m, m, 4, 2, 6, m} };
	static void bfs(){
		int t,i;
		q.add(1);
		for(i=1;i<=6;i++){
			visited[i]=1;
		}
		while(!q.isEmpty()){
			t=q.poll();
			if(t==6)
	        	 break;
			for(i=1;i<=6;i++){
				if( map[t][i]!=m && visited[i]==1){
					visited[i]=0;
					q.add(i);
				}
			}
		}
		for(i=1;i<=6;i++){
			System.out.print(visited[i]+" ");
		}
	}
	/**
	 * @param args
	 */
	public static void main(String[] args) {
		// TODO Auto-generated method stub
		bfs();
	}
}

广度优先搜索算法的应用

广度优先搜索算法能用来解决图论中的许多问题，例如：

• 寻找图中所有连接元件（Connected Component）。一个连接元件是图中的最大相连子图。
• 寻找连接元件中的所有节点。
• 寻找非加权图中任两点的最短路径。
• 测试一图是否为二分图。
• (Reverse) Cuthill–McKee算法

版权声明：本文为博主原创文章，未经博主允许不得转载。