什么是SG？+SG模板

先，定义一下 状态Position P 先手必败 N x先手必胜

操作方法： 反向转移

相同状态 不同位置 的一对 相当于无

对于ICG游戏，我们可以将游戏中每一个可能发生的局面表示为一个点。并且若存在局面i和局面j，且j是i的后继局面(即局面i可以转化为局面j)，我们用一条有向边，从i出发到j，连接表示局面i和局面j的点。则整个游戏可以表示成为一个有向无环图：

根据ICG游戏的定义我们知道，任意一个无法继续进行下去的局面为终结局面，即P局面(先手必败)。在上图中我们可以标记所有出度为0的点为P点。接着根据ICG游戏的两条性质，我们可以逆推出所有点为P局面还是N局面：

对于一个游戏可能发生的局面x，我们如下定义它的sg值：
(1)若当前局面x为终结局面，则sg值为0。
(2)若当前局面x非终结局面，其sg值为：sg(x) = mex{sg(y) | y是x的后继局面}。
mex{a[i]}表示a中未出现的最小非负整数。举个例子来说：
mex{0, 1, 2} = 3, mex{1, 2}=0, mex{0,1,3}=2

我们将上图用sg函数表示后，得到：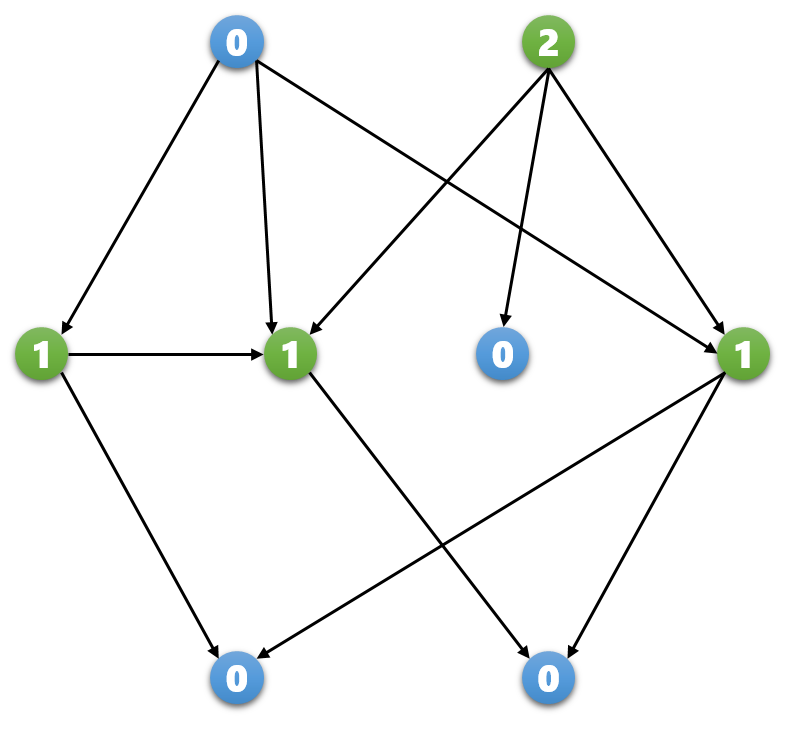

可以发现，若一个局面x为P局面，则有sg(x)=0；否则sg(x)>0。同样sg值也满足N、P之间的转换关系：
若一个局面x，其sg(x)>0，则一定存在一个后续局面y，sg(y)=0。
若一个局面x，其sg(x)=0，则x的所有后续局面y，sg(y)>0。

由上面的推论，我们可以知道用N、P-Position可以描述的游戏用sg同样可以描述。并且在sg函数中还有一个非常好用的定理，叫做sg定理：
对于多个单一游戏，X=x[1..n]，每一次我们只能改变其中一个单一游戏的局面。则其总局面的sg值等于这些单一游戏的sg值异或和。

先定义mex(minimal excludant)运算，这是施加于一个集合的运算，表示最小的不属于这个集合的非负整数。例如mex{0,1,2,4}=3、mex{2,3,5}=0、mex{}=0。

对于一个给定的有向无环图，定义关于图的每个顶点的Sprague-Grundy函数g如下：g(x)=mex{ g(y) | y是x的后继 },这里的g（x）即sg[x]

例如：取石子问题，有1堆n个的石子，每次只能取{1，3,4}个石子，先取完石子者胜利，那么各个数的SG值为多少？

sg[0]=0，f[]={1,3,4},

x=1时，可以取走1-f{1}个石子，剩余{0}个，mex{sg[0]}={0}，故sg[1]=1;

x=2时，可以取走2-f{1}个石子，剩余{1}个，mex{sg[1]}={1}，故sg[2]=0；

x=3时，可以取走3-f{1,3}个石子，剩余{2,0}个，mex{sg[2],sg[0]}={0,0}，故sg[3]=1;

x=4时，可以取走4-f{1,3,4}个石子，剩余{3,1,0}个，mex{sg[3],sg[1],sg[0]}={1,1,0},故sg[4]=2;

x=5时，可以取走5-f{1,3,4}个石子，剩余{4,2,1}个，mex{sg[4],sg[2],sg[1]}={2,0,1},故sg[5]=3；

以此类推.....

x         0  1  2  3  4  5  6  7  8....

sg[x]      0  1  0  1  2  3  2  0  1....

计算从1-n范围内的SG值。

f(存储可以走的步数，f[0]表示可以有多少种走法)

f[]需要从小到大排序

1.可选步数为1~m的连续整数，直接取模即可，SG(x) = x % (m+1);

2.可选步数为任意步，SG(x) = x;

3.可选步数为一系列不连续的数，用GetSG()计算

//f[]：可以取走的石子个数
//sg[]:0~n的SG函数值
//hash[]:mex{}
int f[N],sg[N],hash[N];
void getSG(int n)
{
    int i,j;
    memset(sg,,sizeof(sg));
    for(i=;i<=n;i++)
    {
        memset(hash,,sizeof(hash));
        for(j=;f[j]<=i;j++)
            hash[sg[i-f[j]]]=;
        for(j=;j<=n;j++)    //求mes{}中未出现的最小的非负整数
        {
            if(hash[j]==)
            {
                sg[i]=j;
                break;
            }
        }
    }
}

SG打表

//注意 S数组要按从小到大排序 SG函数要初始化为-1 对于每个集合只需初始化1遍
//n是集合s的大小 S[i]是定义的特殊取法规则的数组
int s[],sg[],n;
int SG_dfs(int x)
{
    int i;
    if(sg[x]!=-)
        return sg[x];
    bool vis[];
    memset(vis,,sizeof(vis));
    for(i=;i<n;i++)
    {
        if(x>=s[i])
        {
            SG_dfs(x-s[i]);
            vis[sg[x-s[i]]]=;
        }
    }
    int e;
    for(i=;;i++)
        if(!vis[i])
        {
            e=i;
            break;
        }
    return sg[x]=e;
}

dfs

注意在SG表的初始化中，不用每次都初始；否则会T的，因为可以循环利用，这是一个强大的地方

HDU1536 实战

#include<stdio.h>
#include<algorithm>
#include<string.h>
using namespace std;
int s[],sg[],n;
char op[];
int SG_dfs(int x)
{
    int i;
    if(sg[x]!=-)
        return sg[x];
    bool vis[];
    memset(vis,,sizeof(vis));
    for(i=;i<n;i++)
    {
        if(x>=s[i])
        {
            SG_dfs(x-s[i]);
            vis[sg[x-s[i]]]=;
        }
    }
    int e;
    for(i=;;i++)
        if(!vis[i])
        {
            e=i;
            break;
        }
    return sg[x]=e;
}
int main()
{
   int k;
    while(scanf("%d",&n)!=EOF)
    {
        if(n==)
        break;
        for(int i= ; i<n ; i++)
        scanf("%d",&s[i]);
        sort(s,s+n);
        int m,cnt=;
        scanf("%d",&m);
        memset(sg,-,sizeof(sg));
        for(int i= ; i<m ; i++)
        {

            scanf("%d",&k);
            int x=;
            while(k--)
            {
                int w;
                scanf("%d",&w);
                x^=SG_dfs(w);

            }
            if(x!=)
            printf("W");
            else
            printf("L");
        }
             puts("");
    }

    return ;
}