数据结构C++使用邻接表实现图

定义邻接表存储的图类。
[实验要求]

（1）创建一个邻接表存储的图；
（2）返回图中指定边的权值；
（3）插入操作：向图中插入一个顶点，插入一条边；
（4）删除操作：从图中删除一个顶点，删除一条边；
（5）图的广度优先遍历；
（6）基于迪杰斯特拉算法求最短路径。【选作】

[截图]

- 实验例图

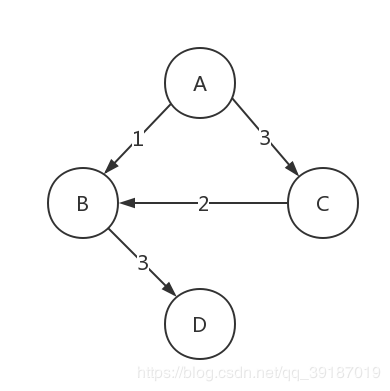
- 邻接表

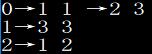
- 操作截图

[实现代码]
一共四个文件 ：AQueue.h、Graph_List.h、Graph_List.cpp和main.cpp

- AQueue.h（自己实现的队列，也可以用C++库中的标准队列需要将代码中的相关代码替换下）

#include<iostream>
using namespace std;
template<class T>
class AQueue {
    private:  int front; /*队首所在数组元素下标*/
    int rear; /*新元素要插入的位置（下标）*/
    int count; /*队列中元素个数*/
    T* QArray; /*存放队列元素的数组*/
    int size; /*存放队列的数组规模*/
    public:  AQueue(int MaxQueueSize = ); /*构造函数*/
    ~AQueue(void) { delete[] QArray; } /*析构函数*/
    bool QInsert(const T& item); /*向队尾插入元素item*/
    bool QDelete(T& item); /*删除队首元素并将该元素值保存至item*/
    void QClear(void) { front = rear = count = ; } /*清空队列*/
    bool QFront(T& item); /*存取队首元素值*/
    bool isEmpty(void)const { return count == ; } /*检测队列是否为空*/
    bool isFull(void)const { return count == size; } /*检测队列是否为满*/
}; 

//构造函数
template<class T>
AQueue<T>::AQueue(int MaxQueueSize)
{
 size = MaxQueueSize;
 QArray = new T[MaxQueueSize];
 front = ; rear = ; count = ;
}

//将元素item插入队尾
template<class T>
bool AQueue<T>::QInsert(const T& item)
{
 if (isFull())
 {
  cout << "Inserting into a full Queue!" << endl;
  return false;
 } //若队列已满
 QArray[rear] = item; //添加队尾元素
 rear = (rear + ) % size; //修改对位指针
 count++; //队列长度+1
 return true;
}

//删除队首元素，并将其元素值赋给变量item
template<class T>
bool AQueue<T>::QDelete(T& item)
{
 if (isEmpty())
 {
  cout << "Deleting from an empty queue！" << endl;
  return false;
 }
 item = QArray[front];
 front = (front + ) % size; //front顺时针移动一格
 count--; //队列长度-1
 return true;
}

//将队首元素值赋给变量item
template<class T>
bool AQueue<T>::QFront(T& item)
{
 if (isEmpty())
 {
  cout << "Reading from an empty queue！" << endl;
  return false;
 }
 item = QArray[front];
 return true;
}

- Graph_List.h

#ifndef _GRAPH_LIST_H
#define _GRAPH_LIST_H
#include<iostream>
using namespace std;
const int maxsize=;
const int maxweight=;
struct Edge{
 friend class Graph_List;
 int VerAdj;
 int cost;
 Edge *link;
};
struct Vertex{
 friend class Graph_List;
 int VerName;
 Edge *adjacent;
};
class Graph_List{
 private:
  Vertex *Head;
  int size;
 public:
  Graph_List();
  virtual ~Graph_List();
  int getweight(const int&v1,const int&v2);
  int getfirstneighbor(const int v);
  int getnextneighbor(const int v1,const int v2);
  void insterVertex(const int&v);
  void insterEdge(const int v1,const int v2,int weight);
  void deleteVertex(const int&v);
  void deleteEdge(const int v1,const int v2);
  void deleteEdge1(const int v1,const int v2);
  void BFS(const int s);
  void DShortestPath(const int v);
  void print();
};
#endif

- Graph_List.cpp

#include<iostream>
#include"Graph_List.h"
#include"AQueue.h"
using namespace std;
Graph_List::Graph_List(){
 int e,from,to,weight;
 Head=new Vertex[maxsize];
 cout<<"输入结点个数："<<endl;
 cin>>size;
 for(int i=;i<size;i++){
  Head[i].VerName=i;
  Head[i].adjacent=NULL;
 }
 cout<<"输入边个数："<<endl;
 cin>>e;
 for(int i=;i<e;i++){
  cout<<"始结点、终止结点、权重："<<endl;
  cin>>from>>to>>weight;
  Edge*p=new Edge;
  p->VerAdj=to;
  p->cost=weight;
  p->link=NULL;
  Edge*q=Head[from].adjacent;
  if(q==NULL)
   Head[from].adjacent=p;
  else{
   while(q->link!=NULL)
    q=q->link;
   q->link=p;
  }
 }
}
Graph_List::~Graph_List(){
 for(int i=;i<size;i++){
  Edge *p=Head[i].adjacent;
  while(p!=NULL){
   Head[i].adjacent=p->link;
   delete p;
   p=Head[i].adjacent;
  }
 }
 delete[]Head;
}
int Graph_List::getweight(const int&v1,const int&v2){
 if(v1==v2) return ;
 if(v1==-||v2==-)return ;
 if(v1>=size||v2>=size)return ;
 Edge *p=Head[v1].adjacent;
 while(p!=NULL){
  if(p->VerAdj==v2)
   return p->cost;
  p=p->link;
 }
 return ;
}
int Graph_List::getfirstneighbor(const int v){
 if(v==-)return -;
 Edge*p=Head[v].adjacent;
 if(p!=NULL)
  return p->VerAdj;
 else
  return -;
}
int Graph_List::getnextneighbor(const int v1,const int v2){
 if(v1!=-&&v2!=-){
  Edge*p=Head[v1].adjacent;
  while(p->VerAdj!=v2&&p!=NULL)
   p=p->link;
  if(p==NULL) return -;
  p=p->link;
  if(p==NULL) return -;
  return p->VerAdj;
 }
}
void Graph_List::insterVertex(const int&v){
 if(v<size&&Head[v].VerName!=-){
  cout<<"此结点已存在"<<endl;
  return;
 }
 size++;
 Head[size-].VerName=v;
 Head[size-].adjacent=NULL;
}
void Graph_List::insterEdge(const int v1,const int v2,int weight){
 Edge*p=Head[v1].adjacent;
 Edge*q=new Edge;
 if(v1==-||v2==-){
  cout<<"结点不存在！"<<endl;
  return;
 }
 if(v1>size){
  cout<<"输入错误！"<<endl;
  return;
 }
 if(v2>size){
  cout<<"输入错误！"<<endl;
  return;
 }
 if(v1==v2){
  cout<<"输入错误！"<<endl;
  return;
 }
 q->VerAdj=v2;
 q->cost=weight;
 if(p==NULL)
   Head[v1].adjacent=q;
 else{
  while(p->link!=NULL)
   p=p->link;
  p->link=q;
 }
 q->link=NULL;
}
void Graph_List::deleteVertex(const int&v){
 if(v>=size){
  cout<<"输入错误！"<<endl;
  return;
 }
 if(Head[v].VerName!=-){
 Edge *p=Head[v].adjacent;
 int i;
 while(p!=NULL){
  Head[v].adjacent=p->link;
  delete p;
  p=Head[v].adjacent;
 }
 Head[v].VerName=-;
 for(i=;i<size;i++){
  if(Head[i].VerName!=-){
   deleteEdge1(i,v);
  }
 }
 size--;
 }
 else
 cout<<"结点不存在！"<<endl;
}
void Graph_List::deleteEdge1(const int v1,const int v2){
 if(v1==v2){
  return;
 }
 Edge *p=Head[v1].adjacent,*q;
 while(p!=NULL){
  if((Head[v1].adjacent)->VerAdj==v2){
   Head[v1].adjacent=p->link;
   delete p;
   return;
  }
  else{
   if(p->VerAdj==v2){
   q->link=p->link;
   delete p;
   return;
  }
  }
  q=p;
  p=p->link;
 }
 if(p==NULL){
  return;
 }
}
void Graph_List::deleteEdge(const int v1,const int v2){
 if(v1==v2){
  cout<<"输入错误！"<<endl;
  return;
 }
 if(v1>=size){
  cout<<"输入错误！"<<endl;
  return;
 }
 if(v2>=size){
  cout<<"输入错误！"<<endl;
  return;
 }
 Edge *p=Head[v1].adjacent,*q;
 while(p!=NULL){
  if((Head[v1].adjacent)->VerAdj==v2){
   Head[v1].adjacent=p->link;
   delete p;
   return;
  }
  else{
   if(p->VerAdj==v2){
   q->link=p->link;
   delete p;
   return;
  }
  }
  q=p;
  p=p->link;
 }
 if(p==NULL){
  cout<<"无此边！"<<endl;
 }
}
void Graph_List::BFS(const int s){
 if(s>=size){
  cout<<"输入错误！"<<endl;
  return;
 }
 int *visited=new int[size];
 for(int k=;k<size;k++)
  visited[k]=;
 cout<<s<<" ";
 visited[s]=;
 AQueue<int>q;
 q.QInsert(s);
 while(!q.isEmpty()){
  int v;
  q.QDelete(v);
  int w=getfirstneighbor(v);
  while(w!=-){
   if(!visited[w]){
    cout<<w<<" ";
    visited[w]=;
    q.QInsert(w);
   }
   w=getnextneighbor(v,w);
  }
 }
 delete []visited;
}
void Graph_List::DShortestPath(const int v){
  int u,k;
  int max=;
  Edge *p;
  int n=size;
  int *path= new int[size];
  int *dist= new int[size];
    int *s=new int[n];//数组是s[i]记录i是否被访问过
 for(int i=;i<n;i++)  {path[i]=-;dist[i]=max;s[i]=; };//数组初始化
  dist[v]=;s[v]=; //初始顶点v的数组值
  p=Head[v].adjacent;
  u=v;
  for(int j=;j<n;j++)
  { //循环（2）：修改u邻接顶点的s【】值path【】值和dist【】值
  while(p!=NULL){
   k=p->VerAdj;
   if(s[k]!=&&dist[u]+p->cost<dist[k])
   {
    dist[k]=dist[u]+p->cost;
    path[k]=u;

   }
   p=p->link;
     } ;
     //循环（3）：修改u邻接顶点的s【】值path【】值和dist【】值
     int ldist=max;
     for(int i=;i<n;i++)
        if(dist[i]>&&dist[i]<ldist&&s[i]==){ldist=dist[i];u=i;     }
  s[u]=;//访问u
  p=Head[u].adjacent;//p为u的边链的头指针
    }
    //for(int i=0;i<n;i++)cout<<path[i]<<" ";
    //cout<<endl;
      for(int i=;i<n;i++)cout<<dist[i]<<" ";
      delete []path;
      delete[] dist;
  }
void Graph_List::print(){
 Edge*p;
 int i;
 for(i=;i<size;i++){
  if(Head[i].VerName!=-){
   cout<<Head[i].VerName;
   p=Head[i].adjacent;
   while(p!=NULL){
    cout<<"→"<<p->VerAdj<<" "<<p->cost<<" ";
    p=p->link;
   }
   cout<<endl;
  }
 }
}

- main.cpp

#include<iostream>
#include"Graph_List.h"
#include"Graph_List.cpp"
using namespace std;
int main(){
 Graph_List a;
 a.print();
 int x,y,z,k;
 cout<<"请选择功能："<<endl;
 cout<<"1.查询权重"<<endl;
 cout<<"2.插入结点"<<endl;
 cout<<"3.插入边"<<endl;
 cout<<"4.删除结点"<<endl;
 cout<<"5.删除边"<<endl;
 cout<<"6.广度优先遍历"<<endl;
 cout<<"7.求最短路径"<<endl;
 while(){
  cout<<"请选择功能："<<endl;
  cin>>k;
  switch(k){
   case :
    cout<<"输入想要查询边的起始、终止结点:"<<endl;
    cin>>x>>y;
    z=a.getweight(x,y);
    cout<<"权重为："<<z<<endl;
    break;
   case :
    cout<<"输入想要插入的结点:"<<endl;
    cin>>x;
    a.insterVertex(x);
    a.print();
    break;
   case :
    cout<<"输入想要插入的边信息:"<<endl;
    cin>>x>>y>>z;
    a.insterEdge(x,y,z);
    a.print();
    break;
   case :
    cout<<"输入想要删除的结点:"<<endl;
    cin>>x;
    a.deleteVertex(x);
    a.print();
    break;
   case :
    cout<<"输入想要删除的边信息:"<<endl;
    cin>>x>>y;
    a.deleteEdge(x,y);
    a.print();
    break;
   case :
    cout<<"输入遍历顶点:"<<endl;
    cin>>x;
    a.BFS(x);
    cout<<endl;
    break;
   case :
    cout<<"输入求最短路顶点:"<<endl;
    cin>>x;
    a.DShortestPath(x);
    cout<<endl;
    break;
  }
 }
 return ;
}