海岸线、科赫曲线、turtle、递归

本章绘图要点：

• turtle模块：python标准库自带的一个模块，可用来绘制二维图形。该模块封装了底层的数据处理逻辑，向外提供了更符合手工绘图习惯的接口函数，适用于绘制对质量、精度要求不高的图形。
• 递归：当所绘制的图形需要多次嵌套重复计算时，可采用递归策略降低程序的复杂性，减少程序的代码量。

海岸线

独上高原，眺望沧海，海洋与陆地之间，蜿蜒而行的海岸线有多长呢？这个问题似乎很简单。按照传统的几何和数学观点，有形状的东西应该都可以被测量。例如，我们可以通过尺子来测量方桌的长和宽，从而获得它的周长。而海岸线虽曲折，但只要测量足够精确，应该就可以得到一个具体的长度。但是问题在于，当用不同大小的度量标准来测量时，每次都会得出完全不同的结果。度量标准的尺度越小，测量出的海岸线长度就会越长，以至于无穷。以1km为单位测量海岸线时，近似长度短于1km的迂回曲折线就会被忽略掉，而以1m为单位测量时，则能测出这些被忽略掉的迂回曲折，长度将变大。以此类推，测量单位越小，测得的长度将越大，这些越来越大的长度并不是趋近于一个确定值，而是会无限增大，所以海岸线的长度是不确定的，或者说，在一定意义上海岸线的长度是无穷的。

为什么会这样呢？这是因为作为海洋与陆地的分界线，海岸线的形状是极不规则、极不光滑的。海岸线由无数的曲线组成，假设我们用一把固定长度的直尺，例如米尺来测量的话，海岸线上两点间小于一米的曲线，就只能用直线来近似地表示，因此，测得的长度肯定是不精确的。使用更短的尺子来量，同样也无法测量更细小的曲线。哪怕我们有一把1纳米长（1纳米大约是1米的10亿分之一）的尺子，情况依旧如此。长度也许已不能正确地概括海岸线这类不规则图形的特征。

海岸线虽然很复杂，但是却有一个重要的性质——自相似性。从不同比例尺的地形图上，我们可以看出海岸线的形状大体相同，其曲折、复杂程度也很相似，也就是说，海岸线的任一小部分都包含有与整体相同或相似的细节。如果将一段海岸线的曲线加以放大，我们会发现，这部分放大的曲线（我们称之为A曲线）与更大范围内的海岸线形状惊人地相似。如果继续放大A曲线中更小的一段，这一小段曲线的形状又与A曲线有相似性。换句话说，任意一段海岸线就象是整个海岸线按比例缩小的结果。

科赫（Koch）曲线

我们可以在计算机上生成科赫曲线来模拟海岸线。科赫曲线是瑞典数学家科赫在1904年提出的一种不规则的几何图形。它的生成方法是把一条直线等分成三段，将中间的一段用夹角为60度的两条等长折线来替代，形成一个生成元，然后再把每个直线段都用生成元来进行替换，如此经过无穷多次迭代后就呈现出了一条有无穷多弯曲的科赫曲线。如图所示：

第一次迭代（生成元）：

第二次迭代：

第三次迭代：

第六次迭代：

可以看到多次迭代后的科赫曲线由无数的曲线组成。与海岸线一样，科赫曲线的局部与整体相似，也就是说，局部是整体的缩影。

算法

我们可以在计算机上用以下方法递归生成Koch曲线：

将线段三等分，描画完第一个三分之一段后逆时针方向旋转60度，接着描画三分之一段长度，再顺时针方向旋转120度，描画三分之一段长度，再逆时针方向旋转60度，描画最后三分之一段长度。

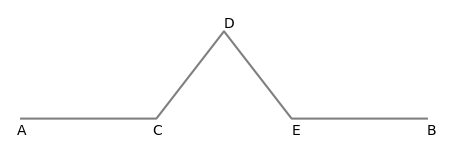
结合上图就是：

1)       初始：起始点A，角度为0；假设线段AB长度为L；

2)       线段三等分，每一段长度为L/3，从点A开始，向前描画L/3长度到达C点；

3)       逆时针方向（也就是向左）旋转60度，向前描画L/3长度，到达D点；

4)       顺时针方向（也就是向右）旋转120度，向前描画L/3长度，到达E点；

5)       逆时针方向（也就是向左）旋转60度，向前描画L/3长度，到达结束点：B点。

源码

 1 # 导入模块
 2 import turtle
 3
 4 # 恢复海龟状态到p点
 5 def restore(p):
 6       turtle.penup()  # 抬起海龟画笔
 7       turtle.setpos(p[0],p[1]) # 移动到p点
 8       turtle.pendown() # 放下画笔
 9       turtle.seth(p[2])   # 设置海龟方向
10
11 # 获取海龟当前点状态
12 def get_point():
13     x,y = turtle.pos()  # 获取海龟的位置
14     d = turtle.heading() # 获取海龟的方向
15     return (x,y,d)
16
17 # 生成器函数，A为起始点，B为结束点，L为线段AB的长度，n为递归次数
18 def Generator(A,B,L,n):
19       if n == 1:
20          # 绘制图形
21          restore(A)
22          turtle.forward(L/3) # 画笔向前移动L/3距离
23          turtle.left(60)      # 画笔方向向左旋转60度（也就是逆时针旋转）
24          turtle.forward(L/3)
25          turtle.right(120)    # 向右旋转120度（也就是顺时针旋转）
26          turtle.forward(L/3)
27          turtle.left(60)
28          turtle.setpos(B[0],B[1]) # 移动到B点，并画线
29       else:
30          # 获取中间点：C、D、E的位置和方向，不显示图形
31          restore(A)
32          turtle.pencolor((59,209,207)) # 画笔颜色设置和背景色相同
33          turtle.forward(L/3)
34          turtle.left(60)
35          C = get_point()
36          turtle.forward(L/3)
37          turtle.right(120)
38          D = get_point()
39          turtle.forward(L/3)
40          turtle.left(60)
41          E = get_point()
42          turtle.pencolor('white') # 画笔颜色设置为白色
43
44          # 递归调用生成器，使用生成元替换线段AC、CD、DE、EB
45          Generator(A,C,L/3,n-1)
46          Generator(C,D,L/3,n-1)
47          Generator(D,E,L/3,n-1)
48          Generator(E,B,L/3,n-1)
49
50       return True
51
52 # 开始主程序
53 if __name__ == '__main__':
54    # 隐藏画笔形状
55    turtle.hideturtle()
56    # 设置颜色模式
57    turtle.colormode(255)
58    # 设置背景色为海蓝色
59    turtle.bgcolor((59,209,207))
60    # 设置画笔颜色为白色
61    turtle.pencolor('white')
62    # 设置画笔大小
63    turtle.pensize(2)
64
65    # 设置初始值
66    A = (-450,0,0)
67    B = (450,0,0)
68    L = 900
69    n = 6
70
71    # 生成科赫曲线
72    restore(A)
73    Generator(A,B,L,n)

 

科赫曲线彩图（海蓝色RGB（59,209,207）/白色）

程序剖析

turtle模块

turtle模块是python标准库自带的一个模块，用于绘制二维图形。在使用之前，需要使用import turtle语句导入该模块。

turtle在英文中的含义是海龟，想象一下，在画布的中间，有一只海龟，四处行走，走过的痕迹就绘成了图形。在画布中，海龟的位置是以二维笛卡尔坐标的方式来确定的，也就是x-y轴坐标，如下图：

海龟的初始位置在原点(0,0)处。海龟的状态除了位置以外，还有一个方向，方向以与水平的角度来确定，逆时针的角度为正数，顺时针的角度为负数。海龟的初始方向为0，也就是在原点上，向右朝向x正轴。

所以，海龟的状态可以用一个三元组（x，y，d）来表示，x和y分别代表横坐标和纵坐标，d代表方向。

以下列出了程序中所用到的turtle模块函数：

turtle.hideturtle() # 海龟画笔是有形状的，如果只想看到绘制的图形，可以使用该函数把画笔的形状隐藏起来

turtle.setpos(x,y)  # 移动海龟到指定位置，

使用turtle.setpos(x,y)改变海龟的位置，默认情况会在画布上留下痕迹，也就是一条直线。要想不留下痕迹，就必须把海龟画笔抬起来，函数是：turtle.penup()，到达指定位置后，把画笔放下来，函数是：turtle.pendown()。

turtle.seth(angle)# 海龟方向旋转angle度，这个角度是相对于水平x正轴的，和海龟当前的方向无关

angle为正数，逆时针旋转；angle为负数，顺时针旋转

turtle.pos() # 获取海龟的坐标位置

turtle.heading() # 获取海龟的方向

turtle.pensize(width) # 指定画笔的大小，参数width为一个正整数

turtle.pencolor(color)# 指定画笔的颜色

turtle.bgcolor(color) # 指定画布背景的颜色

pencolor()和bgcolor()函数的参数color可以是字符串，如“red“，”yellow”，“white”等，也可以是一个RGB数字，如（255,255,0），但是，在使用RGB数字前，必须调用colormode()函数指定颜色的模式：

turtle.colormode(255) # 指定颜色的色彩取值范围为0-255的整数

turtle.forward(distance) # 画笔向前移动distance距离

turtle.left(angle)  # 海龟的方向向左旋转angle度，这个角度angle是相对于海龟当前方向的

turtle.right(angle) # 海龟的方向向右旋转angle度，这个角度angle是相对于海龟当前方向的

可以使用python自带的帮助文件，来查看模块函数的具体说明。帮助文件打开的方式：单击开始按钮，选择【所有程序】→【Python 3.6】 → 【Python 3.6 Manuals (32-bit)】，显示窗口如下：

单击“索引”，在输入框中输入turtle，在下拉列表中选择“turtle (module)”，显示窗口如下：

右边文档中包含了turtle模块所有函数的说明和示例。

递归

程序中的Generator()函数使用了递归来生成曲线。在计算机科学中，递归(Recursion)指的是函数的定义中使用函数本身的方法，也就是说，自己调用自己。递归是有去（递去）有回（回归）的。“有去”是指：递归问题可以分解为若干个规模较小，与原问题形式相同的子问题，这些子问题可以用相同的解题思路来解决；“有回”是指：问题由大到小、层层分解，会到达一个明确的终点，从这个终点开始，不再分解，原路返回到原点。

分形图像具有自我相似、自我嵌套的特点，因此非常适合用递归算法来生成。我们来看一下函数Generator(A,B,L,n)的运行过程：

假设n为2，n不等于1，所以执行else子句：

获取中间点：C、D、E的位置和方向，不显示图形

调用函数Generator(A,C,L/3,1)

n等于1，所以执行if子句：

恢复海龟状态到A点，绘制AC段图形

返回到函数Generator(A,B,L,2)

调用函数Generator(C,D,L/3,1)

n等于1，所以执行if子句：

恢复海龟状态到C点，绘制CD段图形

返回到函数Generator(A,B,L,2)

调用函数Generator(D,E,L/3,1)

n等于1，所以执行if子句：

恢复海龟状态到D点，绘制DE段图形

返回到函数Generator(A,B,L,2)

调用函数Generator(E,B,L/3,1)

n等于1，所以执行if子句：

恢复海龟状态到E点，绘制EB段图形

返回到函数Generator(A,B,L,2)

函数Generator(A,B,L,2)结束

数据可视化Tips

颜色

在信息可视化与视觉设计中，颜色、形状与布局构成了最基本的数据编码手段，其中，颜色可以编码大量的数据信息。如何设置可视化元素的颜色？采用什么样的颜色来编码数据信息，也就是如何将数据信息映射到颜色上？这些决定了可视化结果的表达力与视觉美感。

色彩空间（也称色彩模型或色彩系统）是使用一组数值（通常使用3个或4个值）来表示颜色的抽象数学模型。常用的色彩模式有CMYK、RGB以及HSB等等，其中，CMYK是在印刷上使用比较普遍的色彩模式，RGB是常用于计算机的色彩模式，而HSB的色相、饱和度和明度则是基于人眼视觉细胞而设定的。不同的色彩模式之间通常存在有损或无损的数学转换关系。

计算机采用的RGB色彩模式，R代表red(红 )，G代表green(绿)，B代表blue(蓝)。红、绿、蓝叫做三原色，用它们的组合可以表示任何一种颜色。R、G和B的取值范围都是0到255，各有256种取值。通常说的“纯红”，用RGB值表示就是(255，0，0)；“纯绿”用RGB表示为(0，255，0)；“纯蓝”用RGB表示就是(0,0,255)；“黄”色用RGB表示则为(255，255，0)；“青”色用RGB表示则为(0，255，255)； “粉红”色用RGB表示则为(255，0，255)；任意三个值也必定对应一种颜色。如果在RGB模式上再加上一个值，就是RGBA (red, green, blue,
alpha)，RGBA格式的最后一个元素表示颜色的透明度。