Redundant Paths POJ - 3177 把原图变成边—双连通图

无向图概念：（这里的x->y表示x和y之间有一条无向边）
1.桥：对于一个无向图，如果删除某条边后，该图的连通分量增加，则称这条边为桥

比如1->2->3->4这样一个简单得图一共有3个桥，分别是1->2,2->3,3->4

1->2->3->4->1 这样就没有桥，因为删除任意一个边，任意两点还可以互相往来（因为是双向边嘛）

2.割点/割项：对于一个无向图，如果删除某个节点u后，该图的连通分量增加，则节点u为割项或关节点

1->2->3->4 这样的图有2个割点，分别是2，3

1->2->3->4->1这样的图也是没有割点的，删除任意一个点其他点还是可以往来的

3.点-双联通：对于一个连通图，如果任意两点至少存在两条点不重复路径(即在从x走到y，如果删除任意一个其他点还可以从x走到y)，
  则称这个图为点双连通（也就是通常说的的双联通） 这样的图没有割点

4.边-双联通：对于一个连通图，如果任意两点至少存在两条边不重复路径，则称该图为边双连通的

这样的图没有割边

题意：

贝西和牛群被迫从一片标着1..F的牧场走到另一片牧场，他们必须在烂苹果树附近穿过。奶牛现在已经厌倦了经常被迫走一条特定的路，想要建一些新的路，这样它们就可以在任何一对田地之间至少有两条不同的路可选。他们目前在每对字段之间至少有一条路由，并且希望至少有两条路由。

题解：

那我们可以把所有割边都消除了就可以了

我们通过看图可以发现，割边一般是存在在一个点只与其他所有点有且仅有一条无向边

因为题目上已经保证了任意两点之间至少有一条路，所有我们找到所有这样的点，让它们互相连起来就可以了

黑边是原图的，红边是添加后使图变成边-双连通图的

根据上面描述，2，3，4都属于这样的点，我们就需要2条边就可以使它变成双连通图

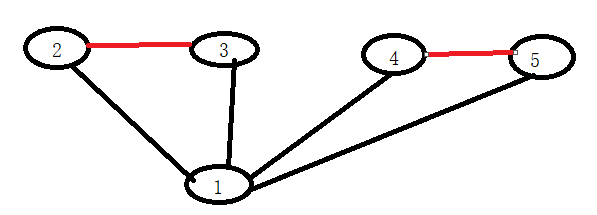
根据上面描述，2，3，4，5都属于这样的点，我们就需要2条边就可以使它变成双连通图

这样的话，任意一个点到达其他点至少有两条路径

代码1：

 1 #include<stdio.h>
 2 #include<string.h>
 3 #include<iostream>
 4 #include<algorithm>
 5 #include<map>
 6 using namespace std;
 7 const int maxn=5010;
 8 int head[maxn],cnt,num,stacks[maxn],top,cut,in[maxn],out[maxn];
 9 struct edge
10 {
11     int v,next;
12 }e[maxn];
13 int visit[maxn],belong[maxn],dfn[maxn],low[maxn];
14 void add_edge(int x,int y)
15 {
16     e[cnt].v=y;
17     e[cnt].next=head[x];
18     head[x]=cnt++;
19 }
20 void init()
21 {
22     memset(in,0,sizeof(in));
23     memset(out,0,sizeof(out));
24     memset(head,-1,sizeof(head));
25     cnt=num=top=cut=0;
26 }
27 void tarjan(int x,int pre)
28 {
29     low[x]=dfn[x]=++num;
30     visit[x]=1;
31     stacks[top++]=x;
32     int flag=1;
33     for(int i=head[x];i!=-1;i=e[i].next)
34     {
35         int v=e[i].v;
36         if(v==pre && flag)
37         {
38             flag=0;
39             continue;
40         }
41         if(!dfn[v])
42         {
43             tarjan(v,x);
44             low[x]=min(low[x],low[v]);
45         }
46         else if(visit[v])
47         {
48             low[x]=min(low[x],dfn[v]);
49         }
50     }
51     if(low[x]==dfn[x])
52     {
53         cut++;
54         int v;
55         while(true)
56         {
57             v=stacks[top-1];
58             top--;
59             belong[v]=cut;
60             visit[v]=0;
61             if(v==x) break;
62             //printf("*");
63         }
64     }
65 }
66 int main()
67 {
68     int n,m;
69     init();
70     scanf("%d%d",&n,&m);
71     while(m--)
72     {
73         int x,y;
74         scanf("%d%d",&x,&y);
75         add_edge(x,y);
76         add_edge(y,x);
77     }
78     tarjan(1,-1);
79     //printf("**\n");
80     for(int i=1;i<=n;++i)
81     {
82         for(int j=head[i];j!=-1;j=e[j].next)
83         {
84             int v=e[j].v;
85             if(belong[i]!=belong[v])
86             {
87                 in[belong[v]]++;
88                 out[belong[i]]++;
89             }
90         }
91     }
92     int ans=0;
93     for(int i=1;i<=n;++i)
94     {
95         if(out[i]==1)
96             ans++;
97     }
98     printf("%d\n",(ans+1)/2);
99 }

代码2：

  1 //time 1031MS
  2
  3 //memory 31340K
  4
  5 #pragma comment(linker, "/STACK:1024000000,1024000000")
  6
  7 #include <iostream>
  8
  9 #include <cstdio>
 10
 11 #include <cstdlib>
 12
 13 #include <cstring>
 14
 15 #define MAXN 300015
 16
 17 #define MAXM 4000015
 18
 19 using namespace std;
 20
 21 struct Edge{
 22
 23     int v,next;
 24
 25 }e[MAXM];
 26
 27 int head[MAXN],en;
 28
 29 int head2[MAXN],en2;
 30
 31 int belong[MAXN],dfn[MAXN],low[MAXN],sta[MAXN],top,num,scc;
 32
 33 int in[MAXN],out[MAXN];
 34
 35 bool vis[MAXN];
 36
 37 void init()
 38
 39 {
 40
 41     memset(head,-1,sizeof(head));
 42
 43     memset(vis,0,sizeof(vis));
 44
 45     en = 0;
 46
 47     top = 0;
 48
 49     scc=num = 0;memset(dfn,0,sizeof(dfn));
 50
 51 }
 52
 53 void addedge(int u,int v)
 54
 55 {
 56
 57     e[en].v = v;
 58
 59     e[en].next = head[u];
 60
 61     head[u] = en++;
 62
 63 }
 64
 65 //void addedge2(int u,int v)
 66 //
 67 //{
 68 //
 69 //    edge2[en2].v = v;
 70 //
 71 //    edge2[en2].next = head2[u];
 72 //
 73 //    head2[u] = en2++;
 74 //
 75 //}
 76
 77 void tarjan(int u,int fa)
 78
 79 {
 80
 81     dfn[u] = low[u] = ++num;
 82
 83     sta[++top] = u;
 84
 85     int cnt=0;
 86
 87     for(int i = head[u]; i != -1; i = e[i].next)
 88
 89     {
 90
 91         int v = e[i].v;
 92
 93         if(!dfn[v])
 94
 95         {
 96
 97             tarjan(v,u);
 98
 99             low[u] = min(low[u],low[v]);
100
101         }
102
103         else if (fa==v)
104
105         {
106
107             if (cnt) low[u] = min(low[u],dfn[v]);//重边
108
109             cnt++;
110
111         }
112
113         else low[u] = min(low[u],dfn[v]);
114
115     }
116
117     if(dfn[u]==low[u])
118
119     {
120
121         int x;
122
123         scc++;
124
125         do
126
127         {
128
129             x = sta[top--];
130
131             belong[x] = scc;
132
133         }while(x!=u);
134
135     }
136
137 }
138
139 //void build()
140 //
141 //{
142 //
143 //    en2 = 0;
144 //
145 //    memset(head2,-1,sizeof(head2));
146 //
147 //    for(int i = 1; i <= n; i++)
148 //
149 //    {
150 //
151 //        for(int j = head[i]; j!=-1; j = e[j].next)
152 //
153 //        {
154 //
155 //            int v = e[j].v;
156 //
157 //            if(belong[i]!=belong[v])
158 //
159 //                addedge2(belong[i],belong[v]);
160 //
161 //        }
162 //
163 //    }
164 //
165 //}
166
167 int ans;
168
169 //int dfs(int u,int p)
170 //
171 //{
172 //
173 //    int max1=0,max2=0;
174 //
175 //    for (int i=head2[u];i!=-1;i=edge2[i].next)
176 //
177 //    {
178 //
179 //        int v=edge2[i].v;
180 //
181 //        if (v==p) continue;
182 //
183 //        int tmp=dfs(v,u)+1;
184 //
185 //        if (max1<tmp) max2=max1,max1=tmp;
186 //
187 //        else if (max2<tmp) max2=tmp;
188 //
189 //    }
190 //
191 //    ans=max(ans,max1+max2);
192 //
193 //    return max1;
194 //
195 //}
196 int main()
197 {
198     int n,m;
199     init();
200     scanf("%d%d",&n,&m);
201     while(m--)
202     {
203         int x,y;
204         scanf("%d%d",&x,&y);
205         addedge(x,y);
206         addedge(y,x);
207     }
208     tarjan(1,-1);
209     //printf("**\n");
210     for(int i=1;i<=n;++i)
211     {
212         for(int j=head[i];j!=-1;j=e[j].next)
213         {
214             int v=e[j].v;
215             if(belong[i]!=belong[v])
216             {
217                 in[belong[v]]++;
218                 out[belong[i]]++;
219             }
220         }
221     }
222     int ans=0;
223     for(int i=1;i<=n;++i)
224     {
225         if(out[i]==1)
226             ans++;
227     }
228     printf("%d\n",(ans+1)/2);
229 }
230 //int main()
231 //
232 //{
233 //
234 //    //freopen("/home/qitaishui/code/in.txt","r",stdin);
235 //
236 //    int u,v;
237 //
238 //    while(scanf("%d%d",&n,&m)&&(n+m))
239 //
240 //    {
241 //
242 //        init();
243 //
244 //        //cout<<n<<m<<endl;
245 //
246 //        for(int i = 0; i < m; i++)
247 //
248 //        {
249 //
250 //            scanf("%d%d",&u,&v);
251 //
252 //            if (v==u) continue;
253 //
254 //            addedge(u,v);
255 //
256 //            addedge(v,u);
257 //
258 //            //cout<<u<<" "<<v<<endl;
259 //
260 //        }
261 //
262 //
263 //
264 //        tarjan(1,-1);
265 //
266 //        build();
267 //
268 //        ans=0;
269 //
270 //        dfs(1,-1);
271 //
272 //        printf("%d\n",scc-ans-1);
273 //
274 //    }
275 //
276 //    return 0;
277 //
278 //}