为什么堆化 heapify() 只用 O(n) 就做到了？

heapify()

前面两篇文章介绍了什么是堆以及堆的两个基本操作，但其实呢，堆还有一个大名鼎鼎的非常重要的操作，就是 heapify() 了，它是一个很神奇的操作，

可以用 O(n) 的时间把一个乱序的数组变成一个 heap。

但是呢，heapify() 并不是一个 public API，看：

所以我们没有办法直接使用。

唯一使用 heapify() 的方式呢，就是使用

PriorityQueue(Collection<? extends E> c)

这个 constructor 的时候，人家会自动调用 heapify() 这个操作。

那具体是怎么做的呢？

哈哈源码已经暴露了：

从最后一个非叶子节点开始，从后往前做 siftDown().

因为叶子节点没必要操作嘛，已经到了最下面了，还能和谁 swap？

举个例子：

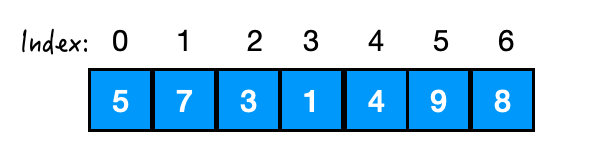
我们想把这个数组进行 heapify() 操作，想把它变成一个最小堆，拿到它的最小值。

那就要从 3 开始，对 3，7，5进行 siftDown().

Step 1.

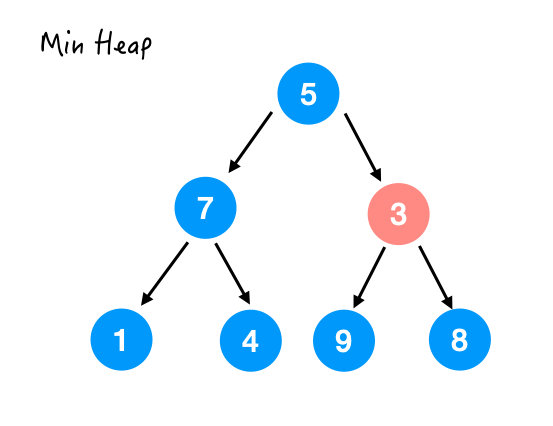
尴尬 ，3 并不用交换，因为以它为顶点的这棵小树已经满足了堆序性。

Step 2.

7 比它的两个孩子都要大，所以和较小的那个交换一下。

交换完成后；

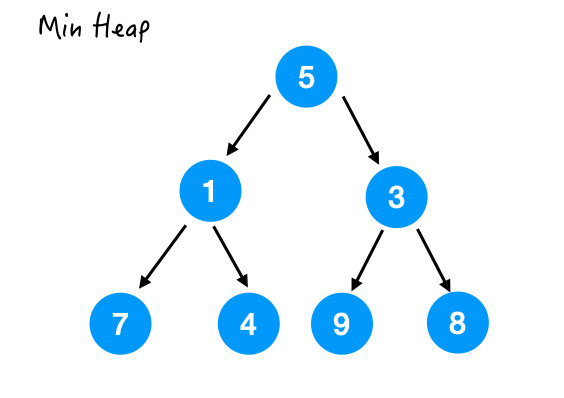
Step 3.

最后一个要处理的就是 5 了，那这里 5 比它的两个孩子都要大，所以也和较小的那个交换一下。

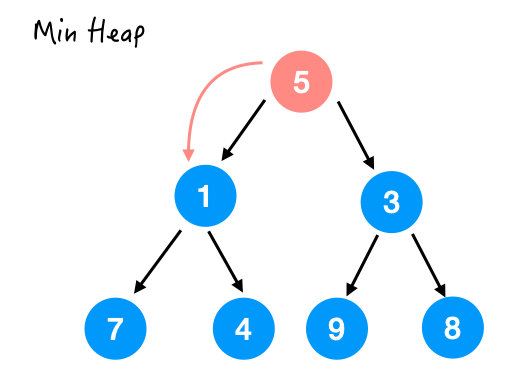
换完之后结果如下，注意并没有满足堆序性，因为 4 还比 5 小呢。

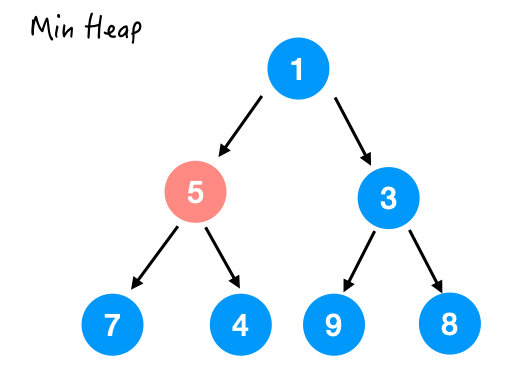
所以接着和 4 换，结果如下：

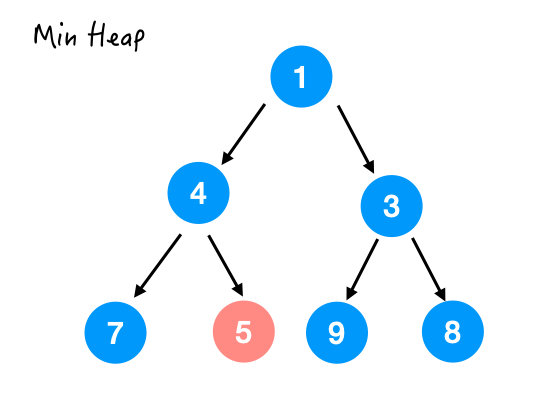
这样整个 heapify() 的过程就完成了。

好了难点来了，为什么时间复杂度是 O(n) 的呢？

怎么计算这个时间复杂度呢？

其实我们在这个过程里做的操作无非就是交换交换。

那到底交换了多少次呢？

没错，交换了多少次，时间复杂度就是多少。

那我们可以看出来，其实同一层的节点最多交换的次数都是相同的。

那么这个总的交换次数 = 每层的节点数 * 每个节点最多交换的次数

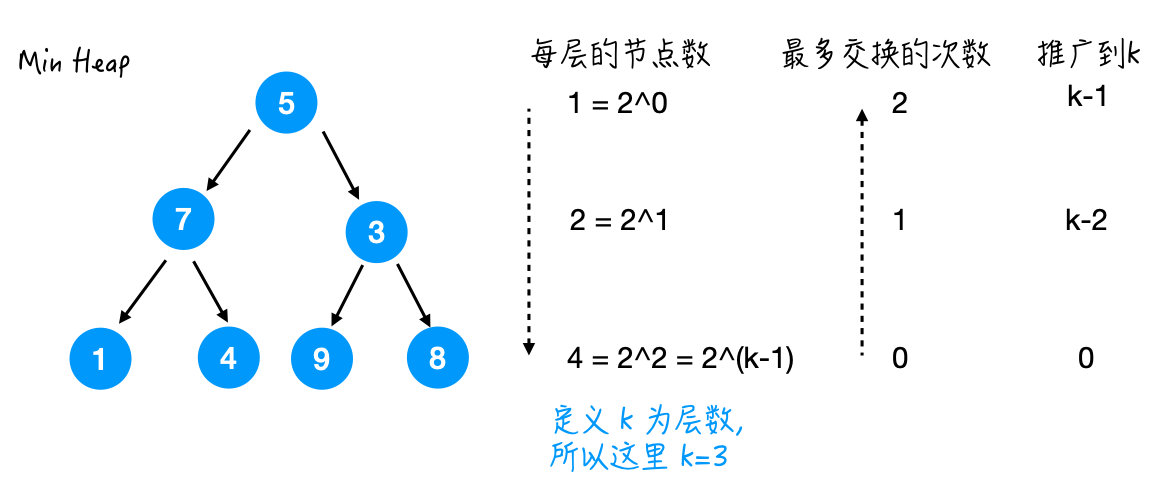
这里设 k 为层数，那么这个例子里 k=3.

每层的节点数是从上到下以指数增长：

$$\ce{1, 2, 4, ..., 2^{k-1}}$$

每个节点交换的次数，

从下往上就是：

$$ 0, 1, ..., k-2, k-1 $$

那么总的交换次数 S(k) 就是两者相乘再相加：

$$S(k) = \left(2^{0} *(k-1) + 2^{1} *(k-2) + ... + 2^{k-2} *1 \right)$$

这是一个等比等差数列，标准的求和方式就是错位相减法。

那么

$$2S(k) = \left(2^{1} *(k-1) + 2^{2} *(k-2) + ... + 2^{k-1} *1 \right)$$

两者相减得：

$$S(k) = \left(-2^{0} *(k-1) + 2^{1} + 2^{2} + ... + 2^{k-2} + 2^{k-1} \right)$$

化简一下：

（不好意思我实在受不了这个编辑器了。。。

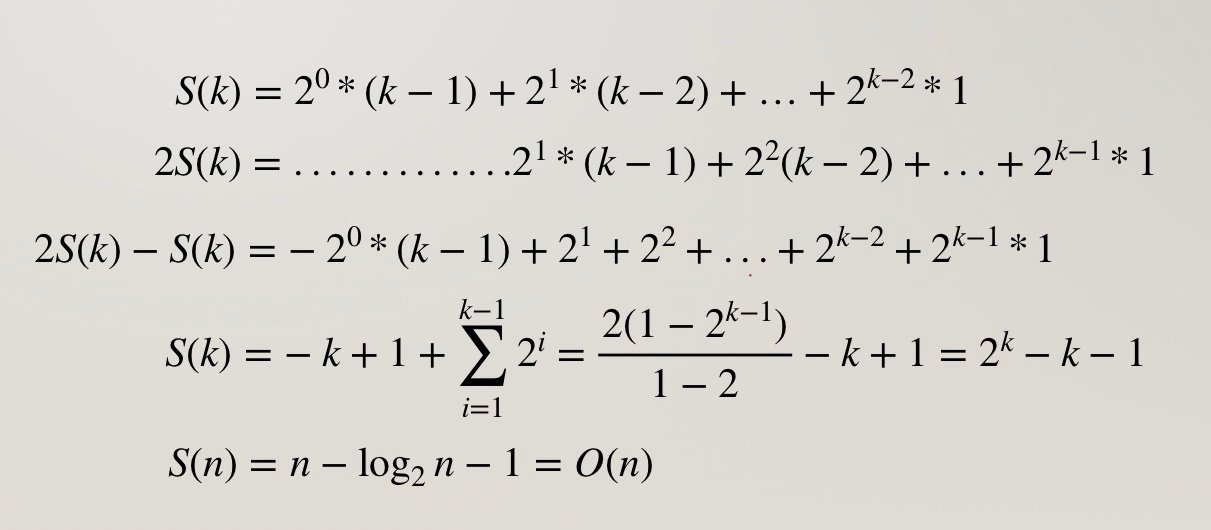
所以 heapify() 时间复杂度是 O(n).

以上就是堆的三大重要操作，最后一个 heapify() 虽然不能直接操作，但是堆排序中用到了这种思路，之前的「选择排序」那篇文章里也提到了一些，感兴趣的同学可以后台回复「选择排序」获得文章～至于堆排序的具体实现和应用，以及为什么实际生产中并不爱用它，我们之后再讲。

如果你喜欢这篇文章，记得给我点赞留言哦～你们的支持和认可，就是我创作的最大动力，我们下篇文章见！

我是小齐，纽约程序媛，终生学习者，每天晚上 9 点，云自习室里不见不散！

更多干货文章见我的 Github: https://github.com/xiaoqi6666/NYCSDE