STL源码剖析：序列式容器

前言

• 容器，置物之所也。就是存放数据的地方。

• array（数组）、list（串行）、tree（树）、stack（堆栈）、queue（队列）、hash table（杂凑表）、set（集合）、map（映像表）…等等。

• 容器按照存储的方式可以分为：序列式容器和关联式容器

• 序列式容器：容器里面的数据可以进行排序，但是不会自动排序，可以使用算法进行排序

• 关联式容器：容器里面的数据不可排序，以键值对的形式存储

Vector

• 和数组类似，区别是数组大小是固定，Vector可以动态改变，不用但是越界的问题

• 动态大小的实现：

  • 当插入数据时，vector检查到数据满了，就会重新申请一块更大的内存，然后将原来的数据拷贝到新申请的内存中，并释放原来的内存

  • 每次重新申请内存时，申请的大小是原来的两倍，以避免多次申请

• vector声明：

template <class T, class Alloc = alloc>
class vector
{
public:
    // 类型相关定义
    typedef T value_type;
    typedef value_type* pointer;
    typedef value_type* iterator;
    typedef value_type& reference;
    typedef size_t size_type;
    typedef ptrdiff_t difference_type;

protected:
    //定义配置器
    typedef simple_alloc<value_type, Alloc> data_allocator;

    iterator start;             // 内存起始地址
    iterator finish;            // 当时使用内存的末尾地址，每次插入和删除都会修改
    iterator end_of_storage;     // 内存的结束地址

    // 关键函数，在某个位置插入一个数据
    void insert_aux(iterator position, const T& x);

    // 使用配置器释放内存
    void deallocate()
    {
        if (start)
            data_allocator::deallocate(start, end_of_storage - start);
    }

    // 申请并初始化一块大小为n的内存，并初始化为value
    void fill_initialize(size_type n, const T& value)
    {
        start = allocate_and_fill(n, value);
        finish = start + n;
        end_of_storage = finish;
    }

public:
    // 迭代器起始位置
    iterator begin() { return start; }
    // 迭代器结束位置
    iterator end() { return finish; }
    // 容器大小，即真实的数据个数
    size_type size() const { return size_type(end() - begin()); }
    // 容器容量，即申请的内存大小
    size_type capacity() const { return size_type(end_of_storage - begin()); }
    // 容器是否为空
    bool empty() const { return begin() == end(); }
    // 重载[]运算符，取出对应position的数据，下标从0开始
    reference operator[](size_type n) { return *(begin() + n); }
    // 构造函数
    vector() : start(), finish(), end_of_storage() {}

    vector(size_type n, const T& value) { fill_initialize(n, value); }

    vector(int n, const T& value) { fill_initialize(n, value); }

    vector(long n, const T& value) { fill_initialize(n, value); }

    explicit vector(size_type n) { fill_initialize(n, T()); }
    // 析构函数
    ~vector()
    {
        destroy(start, finish);
        deallocate();
    }
    // 取出起始数据
    reference front() { return *begin(); }
    // 取出末尾数据
    reference back() { return *(end() - ); }
    // 从尾部插入一个数据
    void push_back(const T& x)
    {
        if (finish != end_of_storage)
        {
            // 内存没有满，直接插入
            construct(finish, x);
            ++finish;
        }
        else
        {
            // 内存满了，需要扩容内存，然后插入数据
            insert_aux(end(), x);
        }
    }

    // 弹出最后一个数据
    void pop_back()
    {
        --finish;
        destroy(finish);
    }

    // 删除时，将后面的数据覆盖前面的数据，然后释放最后一个数据；如果删除的数据是最后一个数据，那么直接
    // 释放即可
    iterator erase(iterator position)
    {
        if (position +  != end())
            // 将position + 1到finish的数据，拷贝到position开始的地方
            copy(position + , finish, position);

        --finish;
        destroy(finish);
        return position;
    }

    // 修改vector的大小，新的size比老的size小，直接删除多余的数据；新的size比老的size大，直接插入
    void resize(size_type new_size, const T& x)
    {
        if (new_size < size())
            erase(begin() + new_size, end());
        else
            insert(end(), new_size - size(), x);
    }
    // 外部统一调用接口，一层封装
    void resize(size_type new_size) { resize(new_size, T()); }
    // 删除容器中所有数据，不会释放内存
    void clear() { erase(begin(), end()); }

protected:
    // 申请并初始化一块内存
    iterator allocate_and_fill(size_type n, const T& x)
    {
        iterator result = data_allocator::allocate(n);
        uninitialized_fill_n(result, n, x);
        return result;
    }
}

Vector迭代器

• Vector维护的是一个线性空间，无论里面元素类型是什么，普通指针都可以作为迭代器，满足统一接口的要求

• 迭代器需要支持的方法：

  • operator*

  • operator->

  • operator++

  • operator--

  • operator+

  • operator-

  • operator+=

  • operator-=

• 上述方法原生指针都支持

• 迭代器类型是：Random Access Iterator

erase方法

// 清除[first,last)的所有元素
iterator erase(iterator first, iterator last)
{
    // 拷贝[last，finish)到[first，first+(finish-last)),返回值是first+(finish-last)
    iterator i = copy(last, finish, first);
    // 析构尾部多余的数据
    destroy(i, finish);
    // 调整finish指针
    finish = finish - (last - first);
    return first;
}

// 清除某个位置的元素,可以理解为erase(iterator first, iterator last)函数中last=first+1
iterator erase(iterator position)
{
    if (position +  != end())
        copy(position + , finish, position);
    --finish;
    destroy(finish);
    return position;
}

insert方法

• 代码解析：

// 从position开始，插入n个元素，元素初值为x
template <class T, class Alloc>
void vector<T, Alloc>::insert(iterator position, size_type n, const T& x)
{
    // 插入元素的个数为0时，直接返回不处理
    if (n != )
    {
        // 剩余的空间大于插入的个数
        if (size_type(end_of_storage - finish) >= n)
        {
            T x_copy = x;
            const size_type elems_after = finish - position;
            iterator old_finish = finish;

            if (elems_after > n)
            {
                 // 插入点到finish的个数大于插入数据的个数
                uninitialized_copy(finish - n, finish, finish);
                finish += n;
                copy_backward(position, old_finish - n, old_finish);
                fill(position, position + n, x_copy);
            }
            else
            {
                // 插入点到finish的个数小于插入数据的个数，需要先在尾部插入，使得插入点到finish的个数                  // 等于插入数据的个数，然后和if分支的处理相同
                uninitialized_fill_n(finish, n - elems_after, x_copy);
                finish += n - elems_after;
                uninitialized_copy(position, old_finish, finish);
                finish += elems_after;
                fill(position, old_finish, x_copy);
            }
        }
        // 剩余空间不够，直接重新申请内存
        else
        {
            const size_type old_size = size();
            const size_type len = old_size + max(old_size, n);

            iterator new_start = data_allocator::allocate(len);
            iterator new_finish = new_start;

            // 以下操作可能失败，所以try一把
            __STL_TRY {
                new_finish = uninitialized_copy(start, position, new_start);
                new_finish = uninitialized_fill_n(new_finish, n, x);
                new_finish = uninitialized_copy(position, finish, new_finish);
            }
            // 定义了__STL_USE_EXCEPTIONS宏就catch，不定义就直接抛异常
            # ifdef __STL_USE_EXCEPTIONS
            catch(...) {
                destroy(new_start, new_finish);
                data_allocator::deallocate(new_start, len);
                throw;
            }
            # endif
            // 释放原来内存，修改3个指针
            destroy(start, finish);
            deallocate();
            start = new_start;
            finish = new_finish;
            end_of_storage = new_start + len;
        }
    }
}

图解

• 剩余的空间大于插入的个数

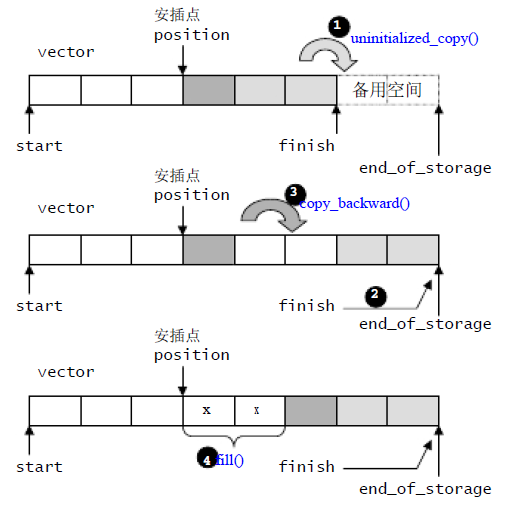
• 插入点到finish的个数小于插入数据的个数

• 剩余空间不够，直接重新申请内存

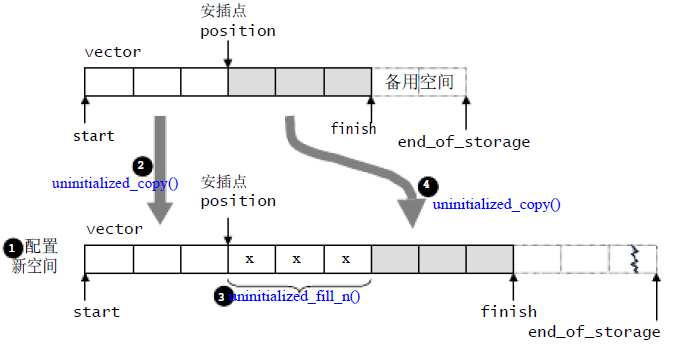
常用方法

• front

• back

• push_back

• pop_back

• erase

• clear

• size

• insert：不建议使用，效率低

List

特点

• 一个双向链表

• 一个成环的双向列表

• 一个有一个门卫节点(空节点)的双向列表

节点定义

template <class T>
struct __list_node
{
    typedef void* void_pointer;
    void_pointer prev; // 指向前一个节点
    void_pointer next; // 指向后一个节点
    T data; // 存储的数据
};

迭代器定义

• 链表的迭代器类型是bidirectional_itrtator

• 内部就是一个__list_node<T>的数据，重载一些操作符，满足STL标准

• 以下代码中包含了迭代器需要重载的所有方法

template<class T, class Ref, class Ptr>
struct __list_iterator
{
    typedef __list_iterator<T, T&, T*> iterator;
    typedef __list_iterator<T, Ref, Ptr> self;

    typedef bidirectional_iterator_tag iterator_category;
    typedef T value_type;
    typedef Ptr pointer;
    typedef Ref reference;
    typedef __list_node<T>* link_type;
    typedef size_t size_type;
    typedef ptrdiff_t difference_type;

    link_type node; // 迭代器内部的核心数据，指向链表中的某一个节点

    // 构造函数
    __list_iterator(link_type x) : node(x) {}

    __list_iterator() {}

    __list_iterator(const iterator& x) : node(x.node) {}

    bool operator==(const self& x) const { return node == x.node; }

    bool operator!=(const self& x) const { return node != x.node; }

    reference operator*() const { return (*node).data; }

    pointer operator->() const { return &(operator*()); }

    // 迭代器++就是下一个节点
    self& operator++()
    {
        node = (link_type)((*node).next);
        return *this;
    }

    self operator++(int)
    {
        self tmp = *this;
        ++*this;
        return tmp;
    }

    // 迭代器--就是上一个节点
    self& operator--()
    {
        node = (link_type)((*node).prev);
        return *this;
    }

    self operator--(int)
    {
        self tmp = *this;
        --*this;
        return tmp;
    }
};

list定义

• list不仅是一个双向串行，而且还是一个环状双向串行。所以它只需要一个数据，便可以完整表现整个链表

template <class T, class Alloc = alloc>
class list
{
protected:
    typedef __list_node<T> list_node;

public:
    typedef list_node* link_type;

protected:
    link_type node; // 核心数据，表示整个链表
    ...
};

• 门卫节点：门卫节点就是一个数据为空的节点，其余和普通节点完全相同

  • 门卫节点在链表初始化的创建

  • 在节点为空时，门卫节点的prev和next都指向自己

  • 门卫节点的下一个节点是头结点，自身是尾节点

• 说明：节点的插入指的是在某节点之前插入

list的相关方法

// 申请一个节点
link_type get_node() { return list_node_allocator::allocate(); }

// 释放一个节点
void put_node(link_type p) { list_node_allocator::deallocate(p); }

// 创建一个节点并初始化
link_type create_node(const T& x)
{
    link_type p = get_node();
    construct(&p->data, x); //
    return p;
}

// 删除一个节点
void destroy_node(link_type p)
{
    destroy(&p->data); //
    put_node(p);
}

// 无参构造函数
list() { empty_initialize(); }

void empty_initialize()
{
    node = get_node();
    node->next = node;
    node->prev = node;
}

// 返回头结点
iterator begin() { return (link_type)((*node).next); }

// 放回尾节点
iterator end() { return node; }

// 判断链表是否为空
bool empty() const { return node->next == node; }

// 计算链表的大小
size_type size() const
{
    size_type result = ;
    distance(begin(), end(), result);
    return result;
}

// 返回头文件的数据
reference front() { return *begin(); }

// 返回尾节点的数据
reference back() { return *(--end()); }

// 尾部插入数据
void push_back(const T& x) { insert(end(), x); }

// 头部插入数据
void push_front(const T& x) {insert(begin(), x);}

// 删除头部节点
void pop_front() { erase(begin()); }

// 删除尾节点
void pop_back()
{
    iterator tmp = end();
    erase(--tmp);
}

// 在position前面插入一个节点，数据为x
iterator insert(iterator position, const T& x)
{
    link_type tmp = create_node(x); 

    tmp->next = position.node;
    tmp->prev = position.node->prev;
    (link_type(position.node->prev))->next = tmp;
    position.node->prev = tmp;

    return tmp;
}

// 删除指定位置的节点
iterator erase(iterator position)
{
    link_type next_node = link_type(position.node->next);
    link_type prev_node = link_type(position.node->prev);
    prev_node->next = next_node;
    next_node->prev = prev_node;
    destroy_node(position.node);
    return iterator(next_node);
}

// 清空链表
template <class T, class Alloc>
void list<T, Alloc>::clear()
{
    link_type cur = (link_type) node->next;
    while (cur != node)
    {
        link_type tmp = cur;
        cur = (link_type) cur->next;
        destroy_node(tmp);
    }

    node->next = node;
    node->prev = node;
}

// 将数据为value的节点全部删除
template <class T, class Alloc>
void list<T, Alloc>::remove(const T& value)
{
    iterator first = begin();
    iterator last = end();
    while (first != last)
    {
        iterator next = first;
        ++next;

        if (*first == value)
            erase(first);

        first = next;
    }
}

常用方法

• back

• front

• push_back

• push_front

• pop_front

• pop_back

• insert

• erase

• clear

• size

deque

特点

• 一种双向开口的连续线性空间

• 与vector最大的区别是：deque可以两端插入和弹出，vector只能一端插入

• deuqe底层维护的是一些分段定量的连续空间，对外提供一种按照连续线性空间的访问方法

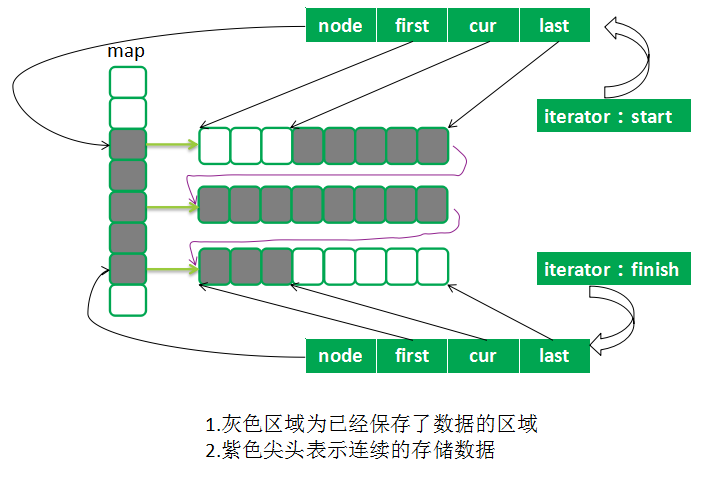
• deque内部唯一个BufSize大小的指针数组，数组中的每一个指针指向一块连续的内存，数据就存放在这些连续的内存中

• deque的中有一个start迭代器和一个finish迭代器，分别指向数据头和数据尾

• deuqe的数据维护如下图所示：

template <class T, class Alloc = alloc, size_t BufSiz = >
class deque {
public:
    typedef T value_type;
    typedef value_type* pointer;
    ...
protected:
    typedef pointer* map_pointer; // map_pointer本质就是T**，一个二重指针

protected:
    ...
}

deque迭代器

• deque迭代器类型是random_access_iterator_tag

• 代码如下：

template <class T, class Ref, class Ptr, size_t BufSiz>
struct __deque_iterator
{
    typedef __deque_iterator<T, T&, T*, BufSiz> iterator;
    typedef __deque_iterator<T, const T&, const T*, BufSiz> const_iterator;
    static size_t buffer_size() {return __deque_buf_size(BufSiz, sizeof(T)); }

    typedef random_access_iterator_tag iterator_category; // (1)
    typedef T value_type;
    typedef Ptr pointer;
    typedef Ref reference;
    typedef size_t size_type;
    typedef ptrdiff_t difference_type;
    typedef T** map_pointer;
    typedef __deque_iterator self;

    // 一下4个数据确定一个数据在deque中的位置
    T* cur;        // 指向连续内存中数据的当前位置
    T* first;    // 指向连续内存的起始位置
    T* last;    // 指向连续内存的结束位置

    map_pointer node; // 指向数组中的某个位置
...
};

// 计算每次申请的连续内存的大小
// n!=0表示大小由用户指定
inline size_t __deque_buf_size(size_t n, size_t sz)
{
    return n !=  ? n : (sz <  ? size_t( / sz) : size_t());
}

// 将迭代器指向数组中一块行的连续空间，注意没有设置cur指针，所以需要单独指定
void set_node(map_pointer new_node) {
    node = new_node;
    first = *new_node;
    last = first + difference_type(buffer_size());
}

reference operator*() const { return *cur; }

pointer operator->() const { return &(operator*()); }

// 计算两个迭代器之间的距离
difference_type operator-(const self& x) const
{
    return difference_type(buffer_size()) * (node - x.node - ) + (cur - first) + (x.last - x.cur);
}

// 前置++

self& operator++()
{
    ++cur;
    if (cur == last)
    {
        set_node(node + );
        cur = first;
    }
    return *this;
}

// 后置++
self operator++(int)
{
    self tmp = *this;
    ++*this;
    return tmp;
}

//前置--
self& operator--()
{
    if (cur == first)
    {
        set_node(node - );
        cur = last;
    }
    --cur;
    return *this;
}

// 后置--
self operator--(int)
{
    self tmp = *this;
    --*this;
    return tmp;
}

// 迭代器跳跃n个距离
self& operator+=(difference_type n)
{
    difference_type offset = n + (cur - first);
    if (offset >=  && offset < difference_type(buffer_size()))
    {
        cur += n;
    }
    else
    {
        difference_type node_offset = offset >  ? offset / difference_type(buffer_size())
: -difference_type((-offset - ) / buffer_size()) - ;

    set_node(node + node_offset);
    cur = first + (offset - node_offset * difference_type(buffer_size()));
    }

    return *this;
}

// 迭代器跳跃n个距离
self operator+(difference_type n) const
{
    self tmp = *this;
    return tmp += n; // 调用operator+=()方法
}

// 迭代器跳跃n个距离，方向是反方向
self& operator-=(difference_type n)
{
    return *this += -n;
}

self operator-(difference_type n) const
{
    self tmp = *this;
    return tmp -= n;
}

// 重载operator[]，内部调用operator+=()方法
reference operator[](difference_type n) const
{
    return *(*this + n);
}

bool operator==(const self& x) const { return cur == x.cur; }

bool operator!=(const self& x) const { return !(*this == x); }

bool operator<(const self& x) const
{
    return (node == x.node) ? (cur < x.cur) : (node < x.node);
}

deque定义

• 内部一个map_pointer指向一个指针数组

• start迭代器指向数据的起始位置

• finish迭代器指向数据的结束位置

• 代码如下：

template <class T, class Alloc = alloc, size_t BufSiz = >
class deque
{
public:
    typedef T value_type;
    typedef value_type* pointer;
    typedef size_t size_type;

public:
    typedef __deque_iterator<T, T&, T*, BufSiz> iterator;

protected:
    typedef pointer* map_pointer;

protected:
    iterator start;
    iterator finish;
    map_pointer map;

    size_type map_size;
    ...
};

iterator begin()
{
    return start;
}

iterator end()
{
    return finish;
}

reference operator[](size_type n)
{
    // 内部调用迭代器的重载[]函数
    return start[difference_type(n)];
}

reference front()
{
    return *start;
} 

reference back()
{
    iterator tmp = finish;
    --tmp;
    return *tmp;
}

size_type size() const { return finish - start; }

type max_size() const { return size_type(-); }

bool empty() const { return finish == start; }

• deque初始化代码如下：

deque(int n, const value_type& value) : start(), finish(), map(), map_size()
{
    fill_initialize(n, value);
}

template <class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::fill_initialize(size_type n, const value_type& value)
{
    create_map_and_nodes(n);
    map_pointer cur;
    __STL_TRY
    {
        for(cur = start.node; cur < finish.node; ++cur)
        {
            //为每个节点设置连续内存块
            uninitialized_fill(*cur, *cur + buffer_size(), value);
        }
        // 为最后一个节点设置连续内存块，可能还有备用空间，因此分别处理
        uninitialized_fill(finish.first, finish.cur, value);
    }
    catch(...)
    {
        ...
    }
}

template <class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::create_map_and_nodes(size_type num_elements)
{
    size_type num_nodes = num_elements / buffer_size() + ;
    map_size = max(initial_map_size(), num_nodes + );
    map = map_allocator::allocate(map_size);

    map_pointer nstart = map + (map_size - num_nodes) / ;
    map_pointer nfinish = nstart + num_nodes - ;
    map_pointer cur;

    __STL_TRY
    {
        // 为每一个节点申请内存
        for(cur = nstart; cur <= nfinish; ++cur)
            *cur = allocate_node();
    }
    catch(...)
    {
        ...
    }

    start.set_node(nstart);
    finish.set_node(nfinish);
    start.cur = start.first;
    finish.cur = finish.first + num_elements % buffer_size();
}

push_back, push_front代码

void push_back(const value_type& t) {
    if (finish.cur != finish.last - )
    {
        construct(finish.cur, t);
        ++finish.cur;
    }
    else
    {
        push_back_aux(t);
    }
}

template <class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::push_back_aux(const value_type& t)
{
    value_type t_copy = t;
    reserve_map_at_back(); // 关键函数：修改数组大小并拷贝数据
    *(finish.node + ) = allocate_node();

    __STL_TRY
    {
        construct(finish.cur, t_copy);
        finish.set_node(finish.node + );
        finish.cur = finish.first;
    }
    __STL_UNWIND(deallocate_node(*(finish.node + )));
}

void push_front(const value_type& t)
{
    if(start.cur != start.first)
    {
        construct(start.cur - , t);
        --start.cur;
    }
    else
    {
        push_front_aux(t);
    }
}

template <class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::push_front_aux(const value_type& t)
{
    value_type t_copy = t;
    reserve_map_at_front(); // 关键函数：修改数组大小并拷贝数据
    *(start.node - ) = allocate_node();

    __STL_TRY
    {
        start.set_node(start.node - );
        start.cur = start.last - ;
        construct(start.cur, t_copy);
    }
    catch(...)
    {
        start.set_node(start.node + );
        start.cur = start.first;
        deallocate_node(*(start.node - ));
        throw;
    }
}

void reserve_map_at_back (size_type nodes_to_add = )
{
    if(nodes_to_add +  > map_size - (finish.node - map))
        reallocate_map(nodes_to_add, false);
}

void reserve_map_at_front (size_type nodes_to_add = )
{
    if(nodes_to_add > start.node - map)
        reallocate_map(nodes_to_add, true);
}

// 类似vector扩容，共3步，只移动数组中的数据，指针指针指向的内存片段里面的数据不动
// 1. 申请一块行的内存
// 2. 将原来的数据拷贝到新的内存中
// 3. 释放原来的内存
template <class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::reallocate_map(size_type nodes_to_add, bool add_at_front)
{
    size_type old_num_nodes = finish.node - start.node + ;
    size_type new_num_nodes = old_num_nodes + nodes_to_add;
    map_pointer new_nstart;

    // 数组足够大，不用重新申请，直接拷贝
    if (map_size >  * new_num_nodes)
    {
        new_nstart = map + (map_size - new_num_nodes) /  + (add_at_front ? nodes_to_add : );
        if (new_nstart < start.node)
        {
            copy(start.node, finish.node + , new_nstart);
        }
        else
            copy_backward(start.node, finish.node + , new_nstart + old_num_nodes);
        }
    else
    {
        // 原来的数组不够，重新申请，拷贝，再释放
        size_type new_map_size = map_size + max(map_size, nodes_to_add) + ;
        map_pointer new_map = map_allocator::allocate(new_map_size);
        new_nstart = new_map + (new_map_size - new_num_nodes) /  + (add_at_front ? nodes_to_add : );

        copy(start.node, finish.node + , new_nstart);
        map_allocator::deallocate(map, map_size);
        map = new_map;
        map_size = new_map_size;
     }

    start.set_node(new_nstart);
    finish.set_node(new_nstart + old_num_nodes - );
}

pop_back，pop_front代码

void pop_back()
{
    if(finish.cur != finish.first)
    {
        --finish.cur;
        destroy(finish.cur);
    }
    else
    {
        pop_back_aux();
    }
}

// 跨行处理，释放内存，调整finish指针
template <class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::pop_back_aux()
{
    deallocate_node(finish.first);
    finish.set_node(finish.node - );
    finish.cur = finish.last - ;
    destroy(finish.cur);
}

void pop_front()
{
    if(start.cur != start.last - )
    {
        destroy(start.cur);
        ++start.cur;
    }
    else
    {
        pop_front_aux();
    }
}

// 跨行处理，释放内存，调整start指针
template <class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::pop_front_aux()
{
    destroy(start.cur);
    deallocate_node(start.first);
    start.set_node(start.node + );
    start.cur = start.first;
}

clear代码

template <class T, class Alloc, size_t BufSize>
void deque<T, Alloc, BufSize>::clear()
{
    // 释放中间数据存储满的内存块
    for (map_pointer node = start.node + ; node < finish.node; ++node)
    {
        destroy(*node, *node + buffer_size());
        data_allocator::deallocate(*node, buffer_size());
    }

    // start和finish不指向同一块内存
    if (start.node != finish.node)
    {
        destroy(start.cur, start.last); // 析构start内存块中的数据
        destroy(finish.first, finish.cur); // 析构finish内存块中的数据
        data_allocator::deallocate(finish.first, buffer_size()); // 释放finish内存块，注意保留了start内存块的数据
    }
    else
    {
         // start和finish指向同一块内存
        destroy(start.cur, finish.cur);
    }

    // 调整状态
    finish = start;
}

insert代码

iterator insert(iterator position, const value_type& x)
{
    if(position.cur == start.cur)
    {
        // 头插直接复用push_front函数
        push_front(x);
        return start;
    }
    else if (position.cur == finish.cur)
    {
        // 尾插直接复用push_front函数
        push_back(x);
        iterator tmp = finish;
        --tmp;
        return tmp;
    }
    else
    {
        // 其他情况调用insert_aux函数
           return insert_aux(position, x);
    }
}

template <class T, class Alloc, size_t BufSize>
typename deque<T, Alloc, BufSize>::iterator
deque<T, Alloc, BufSize>::insert_aux(iterator pos, const value_type& x)
{
    difference_type index = pos - start;
    value_type x_copy = x;

    if (index < size() / )
    {
        // 插入点距离start指针近，在开头插入一个与头元素相同的数据，然后调用copy拷贝
        push_front(front());
        iterator front1 = start;
        ++front1;
        iterator front2 = front1;
        ++front2;
        pos = start + index;
        iterator pos1 = pos;
        ++pos1;
        copy(front2, pos1, front1);
    }
    else
    {
        // 插入点距离finish指针近，在尾部插入一个与尾元素相同的数据，然后调用copy_backward拷贝
        push_back(back());
        iterator back1 = finish;
        --back1;
        iterator back2 = back1;
        --back2;
        pos = start + index;

        copy_backward(pos, back2, back1);
    }

    *pos = x_copy;
    return pos;
}

Stack

• 底层使用的是deque

• 允许在一个方向上插入、移除和查询

• stack没有迭代器，不允许遍历

• 代码如下：

template <class T, class Sequence = deque<T> >
class stack
{

friend bool operator== __STL_NULL_TMPL_ARGS (const stack&, const stack&);  

friend bool operator< __STL_NULL_TMPL_ARGS (const stack&, const stack&);

public:
    typedef typename Sequence::value_type value_type;
    typedef typename Sequence::size_type size_type;
    typedef typename Sequence::reference reference;
    typedef typename Sequence::const_reference const_reference;

protected:
    Sequence c;  // 存放数据的容器

public:
    // stack是否为空
    bool empty() const
    {
        return c.empty();
    }

    // stack大小
    size_type size() const
    {
        return c.size();
    }

    // 查询栈顶数据
    reference top()
    {
        return c.back();
    }

    // 常函数查询栈顶数据
    const_reference top() const
    {
        return c.back();
    }

    // 栈顶插入数据
    void push(const value_type& x)
    {
        c.push_back(x);
    }

    // 栈顶弹出数据
    void pop()
    {
        c.pop_back();
    }
};

// 判断两个栈的Sequence是否是同一个
template <class T, class Sequence>
bool operator==(const stack<T, Sequence>& x, const stack<T, Sequence>& y)
{
    return x.c == y.c;
}

// 判断两个栈Sequence的大小
template <class T, class Sequence>
bool operator<(const stack<T, Sequence>& x, const stack<T, Sequence>& y)
{
    return x.c < y.c;
}

Queue

• queue底层使用的是deque

• 两端可查询，一端可插入，一端可移除的操作

• queue没有迭代器

• 代码如下：

template <class T, class Sequence = deque<T> >
class queue
{
    friend bool operator== __STL_NULL_TMPL_ARGS (const queue& x, const queue& y);

    friend bool operator< __STL_NULL_TMPL_ARGS (const queue& x, const queue& y);

public:
    typedef typename Sequence::value_type value_type;
    typedef typename Sequence::size_type size_type;
    typedef typename Sequence::reference reference;
    typedef typename Sequence::const_reference const_reference;

protected:
    Sequence c; // 底层容器

public:

    // 队列是否为空
    bool empty() const
    {
        return c.empty();
    }

    // 队列大小
    size_type size() const
    {
        return c.size();
    }

    // 获取队头数据
    reference front()
    {
        return c.front();
    }

    // 常函数获取队头数据
    const_reference front() const
    {
        return c.front();
    }

    // 获取队尾数据
    reference back()
    {
        return c.back();
    }

    // 常函数获取队尾数据
    const_reference back() const
    {
        return c.back();
    }

    // 队尾插入数据
    void push(const value_type& x)
    {
        c.push_back(x);
    }

    // 对头移除数据
    void pop()
    {
        c.pop_front();
    }
};

template <class T, class Sequence>
bool operator==(const queue<T, Sequence>& x, const queue<T, Sequence>& y)
{
    return x.c == y.c;
}

template <class T, class Sequence>
bool operator<(const queue<T, Sequence>& x, const queue<T, Sequence>& y)
{
    return x.c < y.c;
}

Heap

介绍

• 二叉树

  • 二叉树是每个结点最多有两个子树的树结构

• 完全二叉树

  • 完全二叉树是一种特殊的二叉树

  • 定义：在一棵二叉树中，除了最后一层外，其余每一层的节点数都是满的

• 满二叉树

  • 满二叉树是一种特殊的完全二叉树

  • 定义：在一棵二叉树中，每一层的节点数都是满的

• 堆

  • 堆是一种特殊的完全二叉树

  • 父节点的值大于(小于)所有子节点的值

• 最大堆：

  • 最大堆是堆的一种

  • 父节点的值大于所有子节点的值

  • 根节点的值最大

• 最小堆

  • 最小堆是堆的一种

  • 父节点的值小于所有子节点的值

  • 根节点的值最小

• 堆的存储形式：

  • 节点存储，类似链表，每一个节点有两个指针，分别指向两个子节点

  • vector存储：类似数组，从上到下，从左到由，一次将堆中的数据保存vector中即可，具备以下性质

    • 前提：根节点下标是1

    • 节点i的左子节点是2i，右子节点是2i+1

    • 节点i的父节点是i/2

• 堆的存储如图所示：

heap算法

• 最大堆插入

• 第一步：将需要插入的数据放在最下一层的最后一个位置

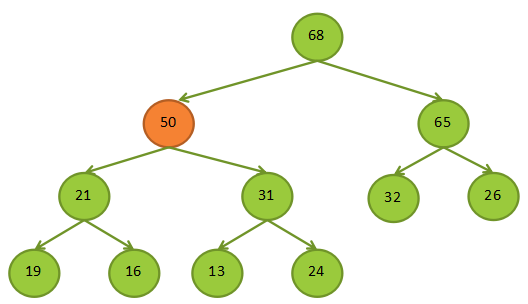
• 第二步：将插入的节点和其父节点比较，如果比父节点大，就父子节点互换，一直向上比较，只到根节点或是父节点比子节点大

• 下图是将50插入堆的流程：

• 最大堆删除
• 堆的删除只能是删除根节点，不能删除非根节点

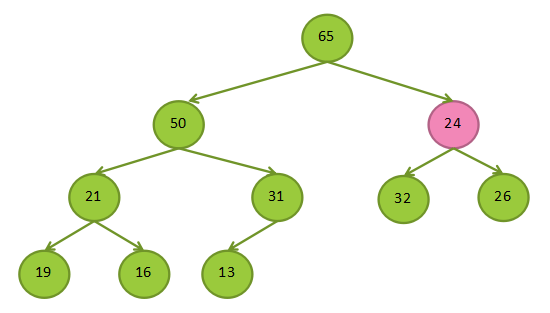
• 第一步：互换根节点和最下面一层最右边的节点

• 第二步：删除最下面一层最右边的节点(原来的根节点)

• 第三步：将根节点与较大的子节点互换，一次向下处理，知道叶子节点，或比左右两个子节点都大

• 下图是将根节点68删除的流程：

push_heap方法

template <class RandomAccessIterator>
inline void push_heap(RandomAccessIterator first, RandomAccessIterator last)
{
    // 注意：在调用此函数时，数据已插入到尾部
    __push_heap_aux(first, last, distance_type(first), value_type(first));
}

template <class RandomAccessIterator, class Distance, class T>
inline void __push_heap_aux(RandomAccessIterator first, RandomAccessIterator last, Distance*, T*)
{
    __push_heap(first, Distance((last - first) - ), Distance(), T(*(last - )));
}

template <class RandomAccessIterator, class Distance, class T>
void __push_heap(RandomAccessIterator first, Distance holeIndex, Distance topIndex, T value)
{
    Distance parent = (holeIndex - ) / ; // 找出父节点
    while (holeIndex > topIndex && *(first + parent) < value)
    {
        // 没有到达根节点，且父节点小于子节点，互换
        *(first + holeIndex) = *(first + parent);
        holeIndex = parent;
        parent = (holeIndex - ) / ;
    } 

    // 将value填入到最后的节点中
    *(first + holeIndex) = value;
}

pop_heap方法

template <class RandomAccessIterator>
inline void pop_heap(RandomAccessIterator first, RandomAccessIterator last)
{
    __pop_heap_aux(first, last, value_type(first));
}

template <class RandomAccessIterator, class T>
inline void __pop_heap_aux(RandomAccessIterator first, RandomAccessIterator last, T*)
{
    __pop_heap(first, last-, last-, T(*(last-)), distance_type(first));
}

template <class RandomAccessIterator, class T, class Distance>
inline void __pop_heap(RandomAccessIterator first, RandomAccessIterator last, RandomAccessIterator result, T value, Distance*)
{
    // 设置尾值为首值
    *result = *first;
    __adjust_heap(first, Distance(), Distance(last - first), value);
}

/*
下面方法的实现流程和前述有点不一致，也可以达到目标，但是比较麻烦
流程：
    1.保存尾节点的值
    2.将头结点的值复制到尾节点，此时头结点为空值
    3.头结点向下，将子节点中较大的节点上移，只到叶子节点
    4.将保存的尾节点值，放入最后的叶子节点
    5.将叶子节点当成新插入的节点进行处理，也就是调用__push_heap
*/
template <class RandomAccessIterator, class Distance, class T>
void __adjust_heap(RandomAccessIterator first, Distance holeIndex, Distance len, T value) {
    Distance topIndex = holeIndex;
    Distance secondChild =  * holeIndex + ;
    while (secondChild < len)
    {
        if (*(first + secondChild) < *(first + (secondChild - )))
            secondChild--;

        *(first + holeIndex) = *(first + secondChild);
        holeIndex = secondChild;
           secondChild =  * (secondChild + );
    }

    if (secondChild == len)
    {
        *(first + holeIndex) = *(first + (secondChild - ));
        holeIndex = secondChild - ;
    }

    __push_heap(first, holeIndex, topIndex, value);
}

sort_heap算法

• 从堆中取出的值，每次都是最大值或是最小值，如果依次取出堆中的值，只到堆为空，将取出的值依次排列，这就是堆排序

• 源码如下：

template <class RandomAccessIterator>
void sort_heap(RandomAccessIterator first, RandomAccessIterator last)
{
    // 核心：循环调用pop_heap方法
    while (last - first > )
        pop_heap(first, last--);
}

make_heap方法

• 作用：用于将容器中的数据，按照堆的规则进行调整

• 源码如下：

// 将 [first,last) 排列为heap。
template <class RandomAccessIterator>
inline void make_heap(RandomAccessIterator first, RandomAccessIterator last)
{
    __make_heap(first, last, value_type(first), distance_type(first));
}

template <class RandomAccessIterator, class T, class Distance>
void __make_heap(RandomAccessIterator first, RandomAccessIterator last, T*,
Distance*)
{
    if (last - first < )
        return; // 如果长度为0或1，不必重新排列

    Distance len = last - first;
    Distance parent = (len - )/; // 最下面一层的节点(叶子节点)不需要处理
    while (true)
    {
        // 对[first,last)中的数据，从倒数第二层开始，依次调用__adjust_heap进行调整
        __adjust_heap(first, parent, len, T(*(first + parent)));

        if(parent == )
            return;
        parent--;
    }
}

Priority_queue

• 底层以最大堆结构实现

• 没有迭代器

• 源码如下：

template <class T, class Sequence = vector<T>, class Compare = less<typename Sequence::value_type> >
class priority_queue
{
public:
    typedef typename Sequence::value_type value_type;
    typedef typename Sequence::size_type size_type;
    typedef typename Sequence::reference reference;
    typedef typename Sequence::const_reference const_reference;

protected:
    Sequence c;        // 底层容器
    Compare comp;    // 元素大小比较标准

public:
    priority_queue() : c() {}

    explicit priority_queue(const Compare& x) : c(), comp(x) {}

    template <class InputIterator>
    priority_queue(InputIterator first, InputIterator last, const Compare& x) : c(first, last), comp(x)
    {
        make_heap(c.begin(), c.end(), comp);
    }

    template <class InputIterator>
    priority_queue(InputIterator first, InputIterator last) : c(first, last)
    {
        make_heap(c.begin(), c.end(), comp);
    }

    bool empty() const
    {
        return c.empty();
    }

    size_type size() const
    {
        return c.size();
    }

    const_reference top() const
    {
        return c.front();
    }

    void push(const value_type& x)
    {
        __STL_TRY
        {
            c.push_back(x);
            push_heap(c.begin(), c.end(), comp); // 泛型算法
        }
        __STL_UNWIND(c.clear());
    }

    void pop()
    {
        __STL_TRY
        {
            pop_heap(c.begin(), c.end(), comp); // 泛型算法
            c.pop_back();
        }
        __STL_UNWIND(c.clear());
    }
};

Slist

• 单向列表

• 不在标准STL的范围内，可以学习

• 相比list，slist有如下特点：

  • slist的插入是在插入点之后插入，不是list的在插入点之前插入

  • slist消耗的空间更小，操作的速度更快

• slist的迭代器是forward iterator迭代器

• 类似list中设计，slist也有一个门卫节点，门卫节点的下一个节点就是链表的头节点

• slist的结构设计如下所示：

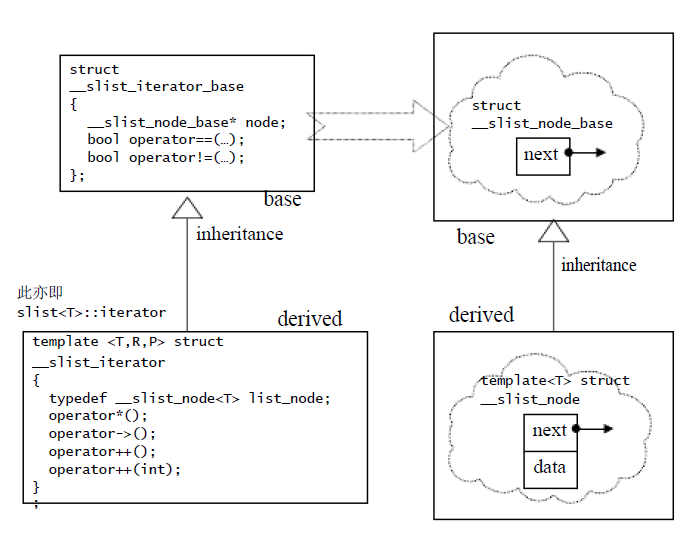
• 节点和迭代器代码如下：

// 节点定义
struct __slist_node_base
{
    __slist_node_base* next;
};

template <class T>
struct __slist_node : public __slist_node_base
{
    T data;
};

inline __slist_node_base* __slist_make_link(__slist_node_base* prev_node,__slist_node_base* new_node)
{
    new_node->next = prev_node->next;
    prev_node->next = new_node;
    return new_node;
}

inline size_t __slist_size(__slist_node_base* node)
{
    size_t result = ;
    for ( ; node != ; node = node->next)
        ++result;
    return result;
}

// 迭代器
struct __slist_iterator_base
{
    typedef size_t size_type;
    typedef ptrdiff_t difference_type;
    typedef forward_iterator_tag iterator_category; 

    __slist_node_base* node; // 核心数据

    __slist_iterator_base(__slist_node_base* x) : node(x) {}

    void incr() { node = node->next; } 

    bool operator==(const __slist_iterator_base& x) const
    {
        return node == x.node;
    }

    bool operator!=(const __slist_iterator_base& x) const
    {
        return node != x.node;
    }
};

template <class T, class Ref, class Ptr>
struct __slist_iterator : public __slist_iterator_base
{
    typedef __slist_iterator<T, T&, T*> iterator;
    typedef __slist_iterator<T, const T&, const T*> const_iterator;
    typedef __slist_iterator<T, Ref, Ptr> self;
    typedef T value_type;
    typedef Ptr pointer;
    typedef Ref reference;
    typedef __slist_node<T> list_node; //核心数据

    __slist_iterator(list_node* x) : __slist_iterator_base(x) {}

    __slist_iterator() : __slist_iterator_base() {}

    __slist_iterator(const iterator& x) : __slist_iterator_base(x.node) {}

    reference operator*() const { return ((list_node*) node)->data; }

    pointer operator->() const { return &(operator*()); }

    self& operator++()
    {
        incr();
        return *this;
    }

    self operator++(int)
    {
        self tmp = *this;
        incr();
        return tmp;
    }

    // 没有operator--
};

• slist定义代码如下：

template <class T, class Alloc = alloc>
class slist
{
public:
    typedef T value_type;
    typedef value_type* pointer;
    typedef const value_type* const_pointer;
    typedef value_type& reference;
    typedef const value_type& const_reference;
    typedef size_t size_type;
    typedef ptrdiff_t difference_type;
    typedef __slist_iterator<T, T&, T*> iterator;
    typedef __slist_iterator<T, const T&, const T*> const_iterator;

private:
    typedef __slist_node<T> list_node;
    typedef __slist_node_base list_node_base;
    typedef __slist_iterator_base iterator_base;
    typedef simple_alloc<list_node, Alloc> list_node_allocator;

    static list_node* create_node(const value_type& x)
    {
        list_node* node = list_node_allocator::allocate();

        __STL_TRY
        {
            // 配置空间
            construct(&node->data, x); // 建构元素
            node->next = ;
        }
        __STL_UNWIND(list_node_allocator::deallocate(node));

        return node;
    }

    static void destroy_node(list_node* node)
    {
        destroy(&node->data); // 将元素解构
        list_node_allocator::deallocate(node); // 释还空间
    }

private:
    list_node_base head; // 头部，门卫节点

public:
    slist() { head.next = ; }

    ~slist() { clear(); }

public:
    iterator begin() { return iterator((list_node*)head.next); }

    iterator end() { return iterator(); } // 需要注意，下面说明

    size_type size() const { return __slist_size(head.next); }

    bool empty() const { return head.next == ; }

    void swap(slist& L)
    {
        list_node_base* tmp = head.next;
        head.next = L.head.next;
        L.head.next = tmp;
    }

public:
    // 取头部元素
    reference front() { return ((list_node*) head.next)->data; }

    void push_front(const value_type& x)
    {
        __slist_make_link(&head, create_node(x));
    }

    void pop_front()
    {
        list_node* node = (list_node*) head.next;
        head.next = node->next;
        destroy_node(node);
    }
    ...
};

• end()方法说明：

  • 表示链表的尾部

  • end()方法返回的是iterator(0)

  • 插入节点时，节点的next指针的值是0，插入链表后会修改，如果是尾节点，那么不会修改，这样保证了链表尾节点的next指针的值永远是0

  • 迭代器在移动的过程中， 移动链表尾部时，迭代器中的值就是0，也就是iterator(0)

  • 所以使用end()方法返回iterator(0)，刚好等于迭代器移动到链表尾部的值