Combining STDP and Reward-Modulated STDP in Deep Convolutional Spiking Neural Networks for Digit Recognition

郑重声明：原文参见标题，如有侵权，请联系作者，将会撤销发布！

Abstract

　　灵长类视觉系统激发了深度人工神经网络的发展，使计算机视觉领域发生了革命性的变化。然而，这些网络的能量效率比它们的生物学对应体要低得多，而且它们通常使用反向传播进行训练，这是非常需要数据的。为了解决这些限制，我们使用了深度卷积脉冲神经网络（DCSNN）和延迟编码方案。我们将最低层的脉冲时序依赖可塑性（STDP）和最高层的奖励调节STDP（R-STDP）结合起来训练。简而言之，在R-STDP中，正确（错误）决策导致STDP（anti-STDP）。这种方法在不需要外部分类器的情况下，对MNIST的准确率为97.2%。此外，我们还证明了R-STDP提取了对当前任务有判断意义的特征，并丢弃了其他特征，而STDP提取了任何重复的特征。最后，我们的方法在生物学上是合理的，硬件友好，而且节能。

Keywords: 脉冲神经网络，深层结构，数字识别，STDP，奖励调节STDP，延迟编码

1 Introduction

　　近年来，深度卷积神经网络（DCNN）在机器视觉领域掀起了一场革命，在许多自然图像的目标识别任务[1]中，DCNN的性能都优于人类视觉。尽管它们有着卓越的性能水平，但对大脑启发的计算模型的研究仍在继续，并吸引着越来越多来自世界各地的研究人员。为了追求这一研究方向，出现了大量基于脉冲神经网络（SNN）的生物学合理性增强模型。然而，SNN在识别精度方面还没能与DCNN竞争。如果DCNN工作良好，那么人们对神经生物学灵感和SNN使用的兴趣增加的原因是什么？

　　首先，能源消耗非常重要。由于经过数百万年进化的优化，人类的大脑消耗了大约20瓦特的电能[2]，大致相当于一台普通笔记本电脑的电能消耗。虽然我们还远未理解这种显著效率的秘密，但基于脉冲信号的处理已经帮助神经形态研究人员设计出了能量效率高的微芯片[3, 4]。

　　此外，随着小型便携式计算设备的出现，采用嵌入式实时系统进行人工智能（AI）非常重要。近年来，专门用于DCNN的实时芯片已经问世，能够快速模拟预训练的网络。然而，由于DCNN的高精度和耗时的操作，采用精确误差反向传播进行在线片上训练还不实用。这个问题使得研究人员修改了误差反向传播算法，使其具有硬件友好性[5]。相反，计算和脉冲通信可以非常快速，适用于低精度平台[6]。此外，生物启发的学习规则，如脉冲时序依赖可塑性（STDP）[7, 8]可以是硬件友好的，也适用于在线片上训练[9]。

　　由于上述原因，加上SNN强大的时空活动域，研究人员尝试了许多不同的方法使SNN在视觉任务中发挥作用。使用分层结构的神经网络是一种常见的方法，但是确定其他参数，如层数、神经元模型、信息编码和学习规则是许多争论的主题。有浅层的[10，11]和深层的[12，13]SNN具有各种类型的连接结构，例如递归的[14]、卷积的[10, 15, 16]和全连接的[17]。信息编码是这场争论的另一个方面，其中基于脉冲率（rate-based）的编码[18, 19, 20]和时间编码[10, 11, 17, 21]是两个主要选项。从反向传播[15, 22, 23, 24]、Tempotron[11, 25]和其他有监督的技术[19, 20, 21, 26, 27]到无监督的STDP及其变体[17, 28]，不同的学习技术也适用于SNN。

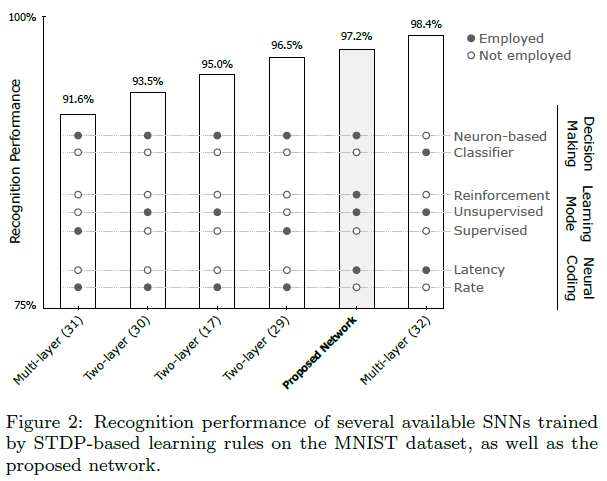
　　关于对大脑灵感的追求，基于STDP的SNN在生物学上是最合理的。利用STDP，网络能够成功地提取出频繁出现的视觉特征。然而，在决策过程中，通常需要外部分类器，如支持向量机（SVM）和径向基函数（RBF）或STDP的有监督变种，单靠无监督学习规则是不够的。有几种基于STDP的SNN已经应用于MNIST数据集的数字识别。例如，Brader et al.[29]的识别成功率为96.5%，Querlioz et al.[30]的识别成功率为93.5%，Diehl and Cook[17]的识别成功率为95%，这些都是在数字识别任务上成功的浅层结构模型。具有深层结构的模型中，Beyer et al.[31]获得了91.6%的不太好的性能，然而，Kheradpisheh et al.[32]训练了一个深度卷积SNN（DCSNN），准确率提高到98.4%。

　　研究人员已经开始探索在SNN和DCNN中使用强化学习（RL）的潜力[33, 34, 35, 36, 37, 38, 39, 40]。RL鼓励学习者重复奖励行为，避免导致惩罚的行为[41]。使用监督学习，网络最多学习监督者所知道的内容，而使用RL，它能够探索环境并学习新技能（任何监督者都不知道），从而提高工作效率和获得奖励[42]。

　　我们先前开发了一种浅层SNN，具有一个可训练层[43]，其中可塑性由奖励调节STDP（R-STDP）控制。R-STDP是受多巴胺（Dopamine，DA）和乙酰胆碱（Acetylcholine，ACh）等神经调节剂在STDP调节中的作用启发的强化学习规则[44, 45]。我们的网络仅根据最后一层的最早脉冲而不使用任何外部分类器来决定对象的类别。结合排序编码和每个神经元最多一个脉冲，我们的网络在生物学上合理、快速、能量效率高，并且硬件友好，在自然图像上有可接受的性能。然而，它的浅层结构使得它不适合于变化幅度大而复杂的数据集。

　　在本研究中，我们设计了一个三层DCSNN，其结构取自[32]，主要用于数字识别。所提出的网络不需要任何外部分类器，使用基于神经元的决策层进行R-STDP训练。首先，输入图像与不同尺度的高斯差分（DoG）滤波器进行卷积。然后，通过强度-延迟编码[46]，产生脉冲波并传播到下一层。在经过多个卷积层和最多允许一次发放的神经元池化层后，脉冲波到达最后一层，那里有预先分配给每个数字的决策神经元。对于每一幅输入图像，最后一层神经元以最早的脉冲时间或最大电位来表示网络的决策。

　　我们在MNIST数据集上评估了我们的DCSNN以进行数字识别。首先，我们只将R-STDP应用于最后一个可训练层，将STDP应用于前两个可训练层，获得了97.2%的识别性能。接下来，我们研究将R-STDP应用于倒数第二个可训练层是否有帮助。我们发现，在输入中存在频繁干扰和计算资源受限的情况下，使用R-STDP代替倒数第二层的STDP是有益的。

　　本文的其余部分组织如下：第2节对所提出的网络的组成部分、突触可塑性和决策提供了精确的描述。然后，在第3节和第4节中，介绍了网络在数字识别任务中的性能以及在多层中应用R-STDP的结果。最后，在第5节中，从不同的角度讨论了所提出的网络，并强调了未来可能的工作。

2 Methods

　　本文的重点是通过结合生物学上合理的学习规则（STDP和R-STDP）来训练和调整DCSNN，以实现数字识别。为此，我们修改了文献[32]中提出的网络，去掉了它的外部分类器（SVM），增加了一个基于神经元的决策层，并使用R-STDP进行突触可塑性研究。这一部分阐述了网络的结构及其组成。

2.1 Overall Structure

　　所提出的网络有六层，即三个卷积层（S1, S2, S3），每个卷积层后面跟着一个池化层（C1, C2, C3）。为了将MNIST图像转换成脉冲波，它们用DoG核进行滤波，并通过强度-延迟方案编码成脉冲时间。卷积层的可塑性由STDP或R-STDP学习规则决定。最终层（C3）是一个全局池化，其中神经元被预先分配给每个数字。这些神经元是网络决策的指示器。图1描绘了提出的网络的轮廓。

　　输入脉冲的产生、每一层的功能、学习规则和决策过程的详细信息在本节的其余部分中给出。

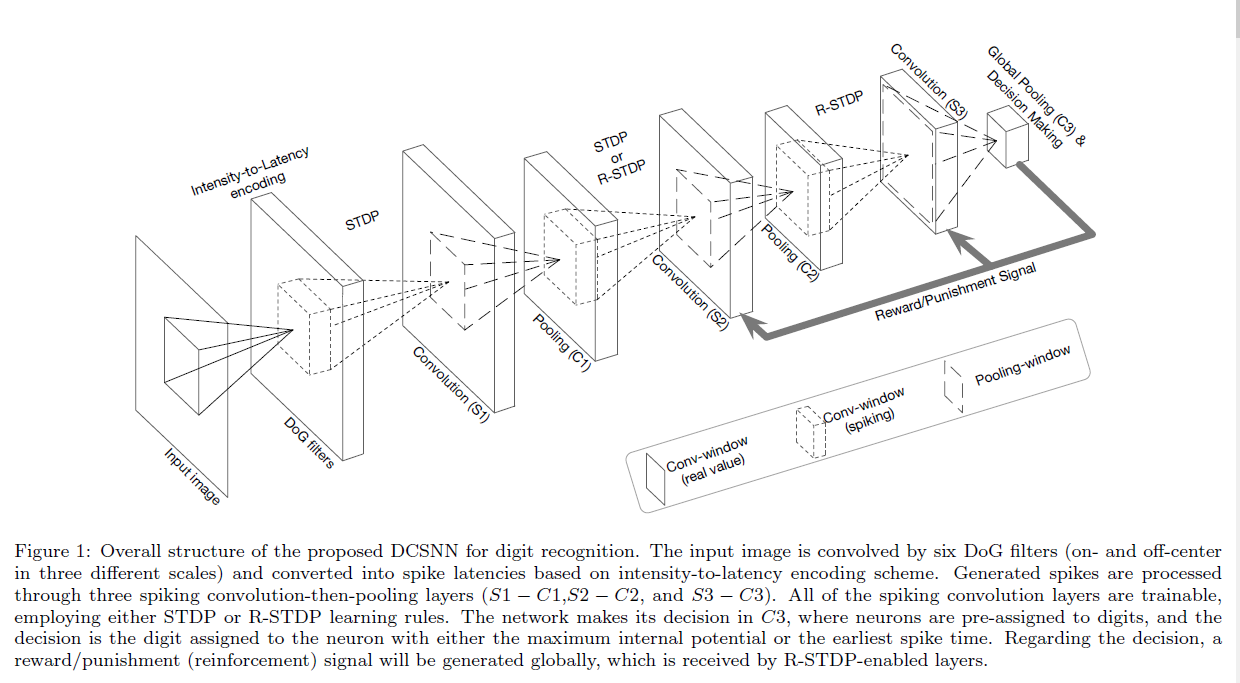
2.2 Input Spike Waves

　　在每个输入图像上，使用三种不同比例的中央和偏离中央的DoG滤波器，并使用零填充。窗口大小设置为3×3、7×7和13×13，其中它们的标准偏差（σ₁、σ₂）分别为（3/9、6/9），（7/9、14/9）和（13/9、26/9）。在每个尺度上，两个σ之间的比值保持为2。这些值实际上是根据输入图像的统计信息选择的。

　　在生成的特征图中，所有50以下的值都被忽略，其余的值都被按降序排序，表示脉冲传播的顺序。

　　为了加快网络并行实现的运行时间，我们将有序输入脉冲平均分配到固定数量的容器中。每个容器中的所有脉冲都是同时传播的。

2.3 Convolutional Layers

　　该网络中的每一个卷积层（S层）包含多个IF神经元的二维网格，称为特征图。S层中的每个神经元都有一个固定的三维输入窗口，其宽度和高度相等，深度等于前一层中的特征图数量。在同一层中，所有神经元的发放阈值被设置为相同。

　　在每一个时间步骤中，输入窗口内刚收到的脉冲对应的突触权重可以增加每个IF神经元的内部电位。这些神经元没有泄露，如果一个神经元达到发放阈值，它将发出一个单一的脉冲，然后保持沉默，直到下一个输入图像被送入网络。对于每一个新的输入，所有神经元的内部电位都重置为零。注意，权重共享机制适用于单个特征图中的所有神经元。

2.4 Pooling Layers

　　我们的网络中使用了池化层（C层）来引入位置不变性和减少信息冗余。每个C层的特征图数目与其前一个S层相同，并且两个层的映射之间存在一对一的关联。

　　在我们的网络中有两种类型的池化层：基于脉冲的和基于电位的。这两种类型都有一个二维输入窗口和一个特定的步长。在基于脉冲和电位的C层中，每个神经元分别表示其输入窗口内神经元的最早脉冲时间和最大电位。

2.5 Decision-Making and Reinforcement Signal

　　如前所述，最终的C层（C3）中的神经元在其相应的S3网格上执行全局池化。这些神经元被标记为输入类别，使得每个C3神经元被分配到单个类别，但每个类别可能被分配到多个神经元。在C3中提供标注神经元，分别使用基于脉冲或基于电位的池化层的情况下，网络对每个输入的决定是有最早脉冲时间或最大内部电位的神经元标签。

　　当网络的决定被指示时，它将与输入图像的原始标签进行比较。如果它们匹配（不匹配），将在全局范围内生成奖惩信号。这个信号将被采用R-STDP突触可塑性规则的层接收（见下一节）。

2.6 Plasticity

　　我们最初用均值为0.8，标准差为0.02的正态分布随机值设置突触权重[32]。STDP和R-STDP学习规则都被用来训练网络中的S层。我们定义了一个通用公式，可用于以下两种规则：

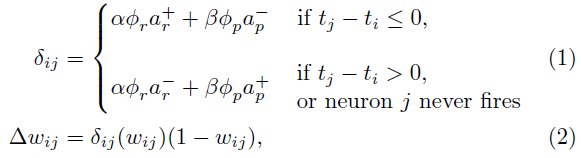
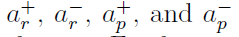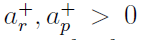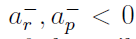其中 i 和 j 分别指突触后和突触前的神经元，Δw_ij是连接这两个神经元的突触的权重变化量，缩放权重变化量。此外，为了指定权重变化的方向，我们设置和。我们的学习规则只需要脉冲时差的符号，而不需要精确值，并且使用一个有限的时间窗口。其他参数，如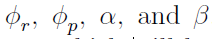，被用作控制因素，每个学习规则的设置不同。

　　在S层上应用STDP，控制因子为φ_r=1、φ_p=0、α=1和β=0。对于R-STDP，α和β的值取决于决策层产生的强化信号。如果产生“奖励”信号，则α=1和β=0；如果产生“惩罚”信号，则α=0和β=1；强化信号也可以是“中性”的，则α=0，β=0。当我们有未标注的数据时，中性信号是有用的。与我们之前的工作类似，我们应用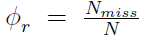和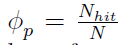来调整系数，其中N_miss和N_hit分别表示在最后一批N个输入样本上正确和错误分类的样本数。请注意，可塑性是针对每个图像进行的，而φ_r和φ_p是在每批样本之后更新的。

　　为了在每个可训练层进行可塑性训练，我们采用了一种k个赢家通吃机制，通过该机制，只有k个神经元才有资格进行可塑性训练。这些神经元不能来自同一个特征图，因为权重共享策略贯穿整个图。选择k个赢家首先基于最早的脉冲时间，然后是较高的内部电位。在训练过程中，当一个赢家被指明时，一个以赢家神经元为中心的r×r抑制窗口将被应用于所有的特征图，防止它们被选为当前输入图像的下一个赢家。

　　此外，我们将项w_ij(1-w_ij)乘以δ_ij，它不仅保持了范围[0, 1]之间的权重，而且随着权重的收敛以稳定权重的变化。

3 Task 1: Solving 10-class Digit Recognition

　　在这项任务中，我们在MNIST数据集的60000幅手写数字图像上训练我们提出的DCSNN。然后在数据集作者提供的10000个未观察样本上测试了网络的识别性能。

3.1 Network Configuration

　　输入层由六个特征图组成，对应于六个DoG滤波器（三个缩放同时具有中央极性和偏离中央极性），每个滤波器都包含脉冲延迟。之后，有三个S层，每个S层后面跟着一个C层，具体参数汇总在表1-3中。

　　前两个S层具有特定的阈值，然而最后一个S层有一个“无限”阈值。这意味着对于输入图像，S3神经元从不发放。相反，它们将所有传入的脉冲积累为它们的内部电位。当没有更多的脉冲积累时，所有的S3神经元将设置一个手动脉冲时间，大于以前的脉冲时间。

　　C1和C2神经元执行基于脉冲的局部池化，而C3神经元应用基于电位的全局池化，这与S3神经元的行为一致。相应地，该网络根据C3神经元之间的最大电位做出决策。换句话说，将选择与具有最大电位的C3神经元相关联的标签作为网络对每个输入图像的决定。

　　值得一提的是，在这项任务中，我们从S3层的可塑性方程中去掉了权重稳定项。相反，我们手动将权重限制在0.2到0.8之间。这种修改是根据我们的实验结果完成的，我们发现即使在后期迭代中，继续突触可塑性也更好。

3.2 Training and Evaluation

　　我们以分层的方式训练网络。用STDP对S1层和S2层分别进行10⁵次和2×10⁵次迭代训练。在每一次迭代中，一幅图像被输入到网络中，每500次迭代后学习率乘以2。当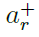小于0.15时，我们继续做乘法运算。

　　S3的训练由R-STDP控制，利用C3层产生的强化信号。我们共训练S3 4×10⁷次迭代，每6×10⁴次迭代，对其识别性能进行评估。我们的网络达到了97.2%的性能，这比以前在MNIST数据集上评估的大多数基于STDP的SNN都要高（见表2）。值得一提的是，我们的网络排名第二，但它没有使用任何外部分类器。它不仅增加了生物学上的合理性，而且增加了网络的硬件友好性[32, 43]。

　　我们还研究了将R-STDP应用于倒数第二个S层（S2）的情况，但是它并没有提高这个特定任务的性能。通过分析R-STDP对S2的影响，我们假设在输入图像中存在频繁干扰且可用计算资源有限的情况下，R-STDP有助于提取目标特定的区分性特征。我们的下一个任务是检验这个假设。

4 Task 2: R-STDP Can Discard Non-Diagnostic Features

　　这项任务的目标是区分两个特定的数字，而其他数字则作为干扰源呈现。这项任务是在MNIST图像的一个子集上进行的，使用一个较小的网络，这使得我们能够分析将R-STDP应用于多个层的优点。本部分首先介绍了一个手工制作的问题和一个简单的两层网络来解决，以便更好的说明。然后，我们使用MNIST数据集的图像显示相同的结果。

4.1 Handmade Problem

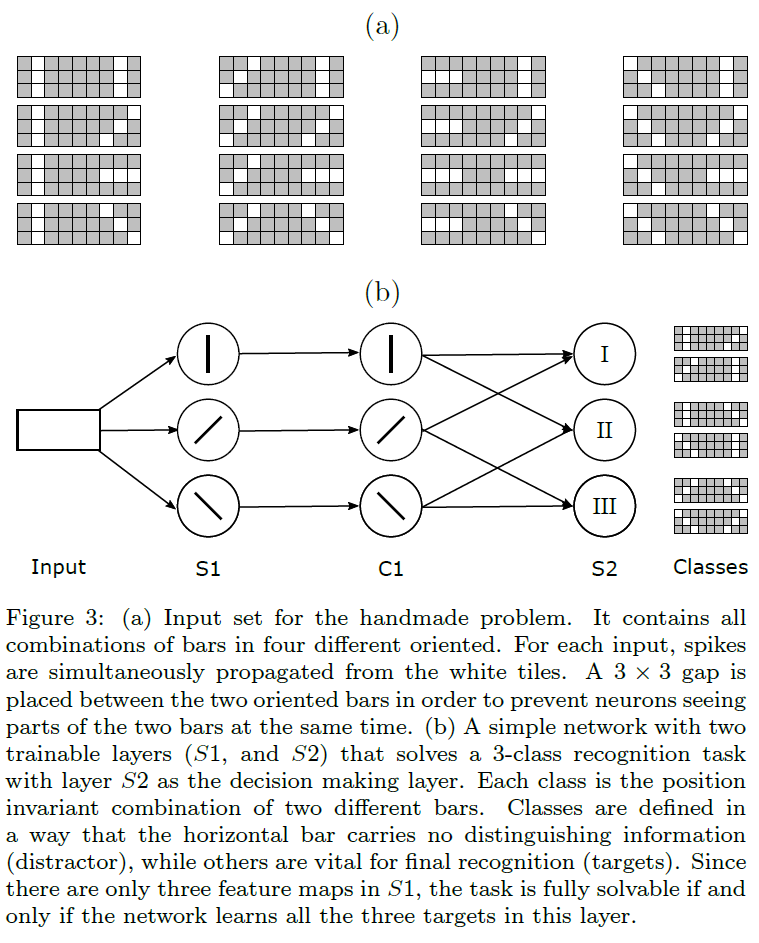
　　我们准备了一组9×3大小的人工图像，每个图像在其最左边和最右边的3×3区域中包含两个定向条。如图3a所示，我们从四个不同方向制作所有可能的条组合。我们通过三个不同方向的条（图3b）的成对组合来描述三类目标输入，将其他输入作为干扰源。所有的输入都以随机顺序输入网络。

　　我们设计了一个最小的两层脉冲网络来区分三个目标类，当且仅当它通过倒数第二个S层（即S1）的神经元学习三条面向判断的线（见图3b）。根据目标类，水平条不携带区分性信息，学习它是对神经元资源的浪费。为此，我们在S1层放置了三个特征图，其神经元具有3×3的输入窗口。在基于脉冲的全局池化层之后，我们放置了三个具有1×1×3的输入窗口的神经元。

　　我们研究了STDP和R-STDP两种学习规则来训练S1，而最后一层总是由R-STDP训练以做出决策。需要注意的是，当我们在两层上使用R-STDP时，两层的可塑性都被推迟到强化信号到达时，因此它们同时被训练。此外，无论网络的判决如何，非目标图像的强化信号都是“中性”的。

　　结果表明，带有STDP训练的S1的网络大多在提取正确方向时失败。相比之下，使用R-STDP训练S1使网络能够在没有任何失败的情况下解决问题。所得结果与STDP的性质一致，即STDP不考虑结果而提取频繁特征。由于每个定向条出现的概率是相同的，因此对于STDP，提取所有判断条的概率是25%（丢弃四者中非区分性特征的概率是1/4）。

　　我们用MNIST数据集实现了类似的任务。在任务的每个实例中，选择两个数字作为目标，另外的数字标记为干扰源。目标是使用少量特征来区分两个目标数字，同时网络接收所有数字的图像。

4.2 Network Configuration

　　层数及其排列与任务1中的网络相同，但是有几个不同之处。首先，MNIST图像在不使用DoG滤波器的情况下输入到网络中。其次，我们在所有的S层中使用了更少的具有不同输入窗口大小和阈值的特征图。第三，S3神经元有特定的阈值以允许它们发放，因此C3执行基于脉冲的全局池化操作。另外，对于每一类，C3中只有一个神经元。参数值汇总在表1-3中。

4.3 Training and Evaluation

　　我们完成了所有数字对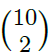（=45对）的任务，S2中不同数量的特征图，范围从2到20。对于每一对，该网络从训练集中训练了10⁴个样本，并测试了每个目标数字的100个测试样本（总共200个测试样本）。用STDP单独训练S1，在S2上检测STDP和R-STDP。S3的可塑性总是由R-STDP控制。

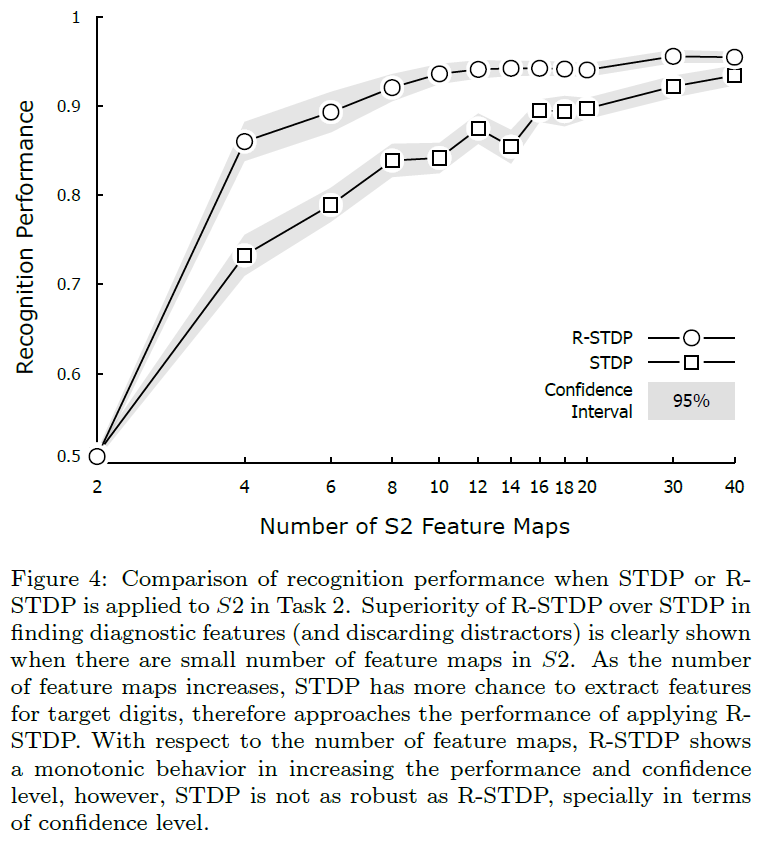
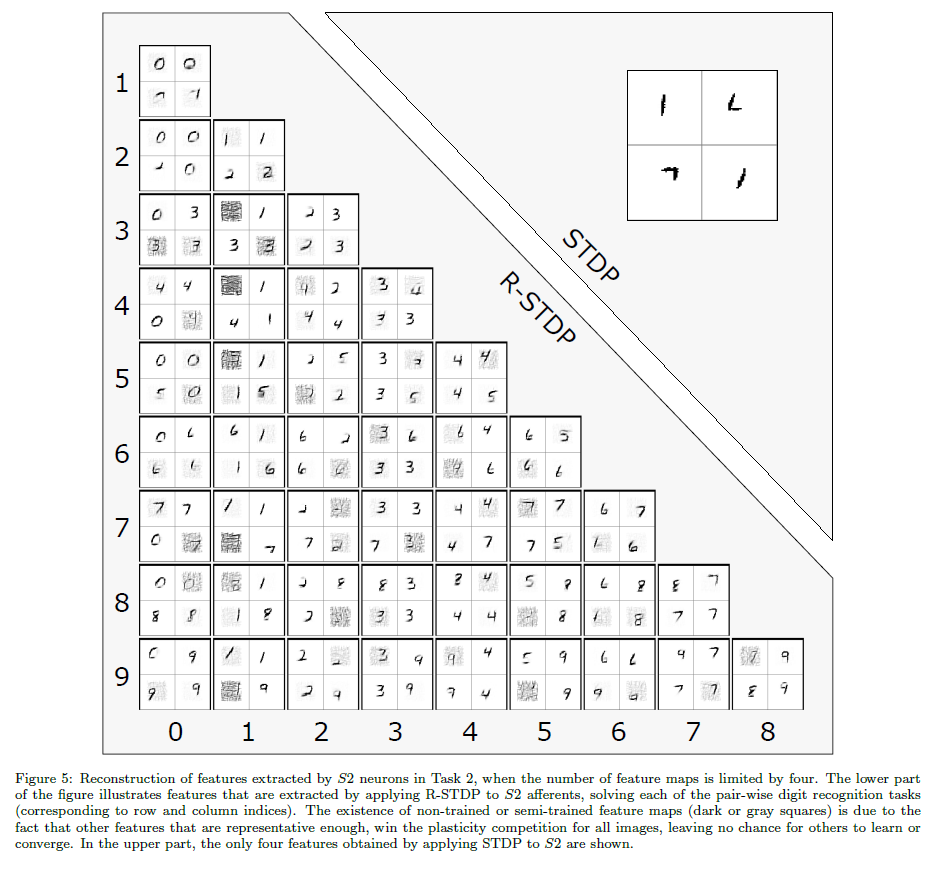
　　对于S2中每个特定数目的特征图，我们计算了在所有数字对上使用STDP和R-STDP两种情况下网络的平均识别性能。如图4所示，实验结果明显支持我们的说法。由于我们的神经元资源较少，使用R-STDP比STDP更有利。然而，通过增加S2中的特征图数量，STDP也有机会扩展区分性特征并填补性能差距。根据图5，R-STDP帮助S2神经元提取目标感知特征。相比之下，使用STDP，S2神经元对目标是盲目的，并且对所有的对提取相同的特征（对所有的任务使用相同的随机种子）。

　　我们承认，如果为每对数字调整其参数，网络可以获得更高的精度。此外，为了在可行的时间内得到大量的仿真结果，我们必须限制迭代次数，并使用更快的学习率，这再次降低了性能。

5 Discussion

　　随着DCNN的出现，人工智能现在能够解决一些复杂的问题，比如视觉目标识别，在该任务中，人类曾经是主宰者[1]。大多数早期的DCNN采用有监督的学习技术来进行特定任务的训练。然而，有监督的学习限制了学习者获得由监督者提供的信息。近年来，研究者发现强化学习将成为新的游戏规则改变者，并开始将DCNN与强化学习技术（又称深度强化学习）相结合。这一组合引入了一些网络，这些网络能够通过查找以前从未被人类测试过的解决方案来实现超人的技能[39, 40, 42]。

　　尽管DCNN在机器视觉领域具有革命性的性能，但SNN在解决复杂视觉任务方面一直处于不断改进之中。SNN并不像DCNN那样完美，但是它们拥有巨大的时空容量，可以填补性能差距，甚至超过DCNN。此外，SNN被证明能源效率高且硬件友好，这使得它们适合部署在AI硬件上[3, 4]。

　　STDP已经成功地应用于SNN的数字识别[17]，但是由于其无监督的特性，需要有监督的读出来实现高精度[32]。除了有监督的读出（如SVM）不受生物学支持之外，它们也不适合硬件实现。

　　本文提出了一种结合STDP和R-STDP学习规则训练的数字识别DCSNN。R-STDP是一个生物学上合理的强化学习规则[44]，同样适用于硬件实现。这种结合受到大脑的启发，在大脑中，突触可塑性大多是无监督的，考虑到突触前和突触后神经元的局部活动，但它可以通过释放神经调节剂进行调节，重新反映从周围环境收到的反馈[7, 8, 44, 45]。

　　该网络利用STDP在早期层提取输入图像的规律性，并利用R-STDP在最后层利用早期层提供的信息学习奖励决策（正确标签）。在所提出的网络的最后一个卷积层使用R-STDP使我们能够使用基于神经元的决策层，而不是复杂的外部分类器。在这个网络中，信息被编码在神经元的最早脉冲时间中。输入图像被多个DoG滤波器卷积，并通过强度-延迟编码方案转换为脉冲延迟。脉冲传播和可塑性是以分层的方式进行的，但所有启用R-STDP的层都是同时训练的。当脉冲波到达决策层时，选择具有最大电位或最早脉冲时间的神经元标签作为网络的决策。将决策结果与输入的原始标签进行比较，全局生成奖惩（强化）信号，该信号调节采用R-STDP学习规则的可训练层的可塑性。

　　首先，我们将我们的网络应用于整个MNIST数据集，只在最后一个可训练层上使用R-STDP。我们的网络达到了97.2%的识别准确率，这比之前提出的基于STDP的SNN要高。然后，通过允许倒数第二个可训练层使用R-STDP，我们研究了在多个层中应用R-STDP是否有帮助。回顾少数不同实验的结果发现，如果输入集受到频繁干扰的污染，则在多个层中应用R-STDP有助于避免干扰，并使用比启用STDP的层更低的计算资源来提取区分性特征。

　　为了提高提出的网络的性能，我们测试了各种配置和参数值。在此，我们调研了关于这些测试结果的发现：

Deciding based on the maximum potential in Task 1. 我们尝试了基于第一步最早脉冲的决策，但结果并不具有竞争力。通过对错误分类样本的研究，我们发现具有共同部分特征的数字是最有问题的数字。例如，数字1和7共享一条倾斜的垂直线（1在MNIST中大部分是倾斜的）。假设一个神经元已经学会产生数字1的最早脉冲。显然，它也会为数字7的许多样本产生最早的脉冲，从而导致高误报警率。因此，我们决定省略阈值，并将最大电位作为决策指标。由于网络必须等到最后一个脉冲，这种方法增加了计算时间，但成功地缓解了上述问题。

R-STDP is only applied to the last layer in Task 1. 正如我们在任务2和之前的工作[43]中所示，当计算资源有限时，R-STDP可以比STDP更好。在任务1中，目标是将网络的性能提高到一个可接受和可竞争的水平。由于MNIST是一个数据集，每个数字的变化范围很大，因此我们必须在每个层放置足够的特征图来覆盖它们。因此，由于特征图的数量庞大，并且输入中没有干扰因素，STDP在提取有用的中间特征方面表现良好。

Learning in the ultimate layer is slower than the penultimate one in Task 2. 在任务2中，S2和S3同时接受训练。如果S3改变突触权重的速度和S2一样快，那么S2中的每一个变化都可能将S3以前良好的行为改变成一个坏的行为，然后破坏S2，这个循环可能永远持续下去，破坏网络的稳定性。

　　该网络继承了之前工作的生物学合理性、能量效率和硬件友好性[32, 43]，现在它能够以更深层的结构解决更难和复杂的识别任务。我们相信我们的DCSNN可以从多个方面进一步改进。

　　如前所述，基于电位的决策降低了计算效率。一种克服由于共同的部分特征而产生的误报警的方法是利用抑制性神经元进行基于脉冲的决策。如果它接收到的东西不止有首要刺激（例如，数字7的水平线，抑制负责数字1的神经元，从而不会产生误报警），抑制性神经元可以抑制一个神经元。另一个方面是通过设计基于组的决策层来提高性能。例如，可以考虑一组最早的脉冲而不是一个脉冲，并进行主要投票，这也可能影响训练策略。未来工作的另一个方向是研究R-STDP在中间层的分层应用，在中间层中，奖惩信号可以基于其他活动度量（如稀疏性、信息内容和多样性）生成。