js 浮点数陷阱

众所周知，JavaScript 浮点数运算时经常遇到会 0.000000001 和 0.999999999 这样奇怪的结果，如 0.1+0.2=0.30000000000000004、1-0.9=0.09999999999999998，很多人知道这是浮点数误差问题，但具体就说不清楚了。本文帮你理清这背后的原理以及解决方案，还会向你解释JS中的大数危机和四则运算中会遇到的坑。

浮点数的存储

首先要搞清楚 JavaScript 如何存储小数。和其它语言如 Java 和 Python 不同，JavaScript 中所有数字包括整数和小数都只有一种类型 — Number。它的实现遵循 IEEE 754 标准，使用 64 位固定长度来表示，也就是标准的 double 双精度浮点数（相关的还有float 32位单精度）。计算机组成原理中有过详细介绍，如果你不记得也没关系。

这样的存储结构优点是可以归一化处理整数和小数，节省存储空间。

64位比特又可分为三个部分：

符号位S：第 1 位是正负数符号位（sign），0代表正数，1代表负数
指数位E：中间的 11 位存储指数（exponent），用来表示次方数
尾数位M：最后的 52 位是尾数（mantissa），超出的部分自动进一舍零

实际数字就可以用以下公式来计算：
$ V = (-1)^{S}\times M \times 2^{E} $

注意以上的公式遵循科学计数法的规范，在十进制是为0<M<10，到二进行就是0<M<2。也就是说整数部分只能是1，所以可以被舍去，只保留后面的小数部分。如 4.5 转换成二进制就是 100.1，科学计数法表示是 1.001*2^2，舍去1后 M = 001。E是一个无符号整数，因为长度是11位，取值范围是 0~2047。但是科学计数法中的指数是可以为负数的，所以再减去一个中间数 1023，[0,1022]表示为负，[1024,2047] 表示为正。如4.5 的指数E = 1025，尾数M为 001。

最终的公式变成：

$ V = (-1)^{S}\times (M+1) \times 2^{E-1023} $

所以 4.5 最终表示为（M=001、E=1025）：

下面再以 0.1 例解释浮点误差的原因， 0.1 转成二进制表示为 0.0001100110011001100(1100循环)，1.100110011001100x2^-4，所以 E=-4+1023=1019；M 舍去首位的1，得到 100110011...。最终就是：

转化成十进制后为 0.100000000000000005551115123126，因此就出现了浮点误差。

为什么 `0.1+0.2=0.30000000000000004`？

计算步骤为：

// 0.1 和 0.2 都转化成二进制后再进行运算

0.00011001100110011001100110011001100110011001100110011010 +

0.0011001100110011001100110011001100110011001100110011010 =

0.0100110011001100110011001100110011001100110011001100111

// 转成十进制正好是 0.30000000000000004

为什么 `x=0.1` 能得到 `0.1`？

恭喜你到了看山不是山的境界。因为 mantissa 固定长度是 52 位，再加上省略的一位，最多可以表示的数是 2^53=9007199254740992，对应科学计数尾数是 9.007199254740992，这也是 JS 最多能表示的精度。它的长度是 16，所以可以使用 toPrecision(16) 来做精度运算，超过的精度会自动做凑整处理。于是就有：

0.10000000000000000555.toPrecision(16)

// 返回 0.1000000000000000，去掉末尾的零后正好为 0.1

// 但你看到的 `0.1` 实际上并不是 `0.1`。不信你可用更高的精度试试：

0.1.toPrecision(21) = 0.100000000000000005551

大数危机

可能你已经隐约感觉到了，如果整数大于 9007199254740992 会出现什么情况呢？
由于 E 最大值是 1023，所以最大可以表示的整数是 2^1024 - 1，这就是能表示的最大整数。但你并不能这样计算这个数字，因为从 2^1024 开始就变成了 Infinity

> Math.pow(2, 1023)

8.98846567431158e+307

> Math.pow(2, 1024)

Infinity

那么对于 (2^53, 2^63) 之间的数会出现什么情况呢？

(2^53, 2^54) 之间的数会两个选一个，只能精确表示偶数
(2^54, 2^55) 之间的数会四个选一个，只能精确表示4个倍数
... 依次跳过更多2的倍数

下面这张图能很好的表示 JavaScript 中浮点数和实数（Real Number）之间的对应关系。我们常用的 (-2^53, 2^53) 只是最中间非常小的一部分，越往两边越稀疏越不精确。

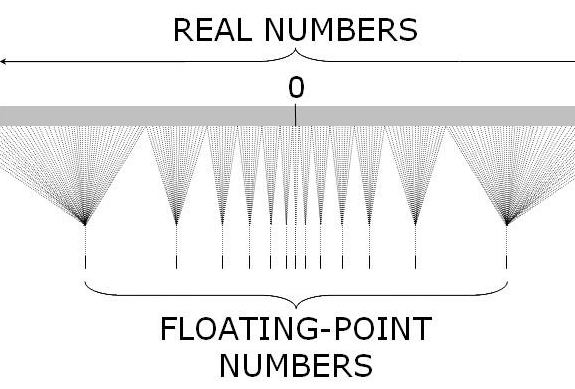
在淘宝早期的订单系统中把订单号当作数字处理，后来随意订单号暴增，已经超过了
9007199254740992，最终的解法是把订单号改成字符串处理。

要想解决大数的问题你可以引用第三方库 bignumber.js，原理是把所有数字当作字符串，重新实现了计算逻辑，缺点是性能比原生的差很多。所以原生支持大数就很有必要了，现在 TC39 已经有一个 Stage 3 的提案 proposal bigint，大数问题有问彻底解决。

`toPrecision` vs `toFixed`

数据处理时，这两个函数很容易混淆。它们的共同点是把数字转成字符串供展示使用。注意在计算的中间过程不要使用，只用于最终结果。

不同点就需要注意一下：

toPrecision 是处理精度，精度是从左至右第一个不为0的数开始数起。
toFixed 是小数点后指定位数取整，从小数点开始数起。

两者都能对多余数字做凑整处理，也有些人用 toFixed 来做四舍五入，但一定要知道它是有 Bug 的。

如：1.005.toFixed(2) 返回的是 1.00 而不是 1.01。

原因： 1.005 实际对应的数字是 1.00499999999999989，在四舍五入时全部被舍去！

解法：使用专业的四舍五入函数 Math.round() 来处理。但 Math.round(1.005 * 100) / 100 还是不行，因为 1.005 * 100 = 100.49999999999999。还需要把乘法和除法精度误差都解决后再使用 Math.round。可以使用后面介绍的 number-precision#round 方法来解决。

解决方案

回到最关心的问题：如何解决浮点误差。首先，理论上用有限的空间来存储无限的小数是不可能保证精确的，但我们可以处理一下得到我们期望的结果。

数据展示类

当你拿到 1.4000000000000001 这样的数据要展示时，建议使用 toPrecision 凑整并 parseFloat 转成数字后再显示，如下：

parseFloat(1.4000000000000001.toPrecision(12)) === 1.4  // True

封装成方法就是：

function strip(num, precision = 12) {

  return +parseFloat(num.toPrecision(precision));

}

为什么选择 12 做为默认精度？这是一个经验的选择，一般选12就能解决掉大部分0001和0009问题，而且大部分情况下也够用了，如果你需要更精确可以调高。

数据运算类

对于运算类操作，如 +-*/，就不能使用 toPrecision 了。正确的做法是把小数转成整数后再运算。以加法为例：

/**

 * 精确加法

 */

function add(num1, num2) {

  const num1Digits = (num1.toString().split('.')[1] || '').length;

  const num2Digits = (num2.toString().split('.')[1] || '').length;

  const baseNum = Math.pow(10, Math.max(num1Digits, num2Digits));

  return (num1 * baseNum + num2 * baseNum) / baseNum;

}

以上方法能适用于大部分场景。遇到科学计数法如 2.3e+1（当数字精度大于21时，数字会强制转为科学计数法形式显示）时还需要特别处理一下。

能读到这里，说明你非常有耐心，那我就放个福利吧。遇到浮点数误差问题时可以直接使用
github.com/dt-fe/numbe…

完美支持浮点数的加减乘除、四舍五入等运算。非常小只有1K，远小于绝大多数同类库（如Math.js、BigDecimal.js），100%测试全覆盖，代码可读性强，不妨在你的应用里用起来！

参考并转载于：https://github.com/camsong/blog/issues/9