题解-NOI2016 优秀的拆分

NOI2016 优秀的拆分

\(T\) 组测试数据。求字符串 \(s\) 的所有子串拆成 \(AABB\) 形式的方案总和。

数据范围：\(1\le T\le 10\)，\(1\le n\le 3\cdot 10^4\)。

---

这道题太神了，能一次做出这题的人往往是人形自走题库。真的全是套路！

---

令 \(n=|s|\)，\(f_i\) 表示有几个以 \(s_i\) 结尾的 \(AA\) 串，\(g_i\) 表示有几个以 \(s_i\) 开头的 \(BB\) 串。

\[\therefore ans=\sum_{i=1}^{n-1}f_i\cdot g_{i+1}
\]

然后只需求 \(f_i,g_i\)。

套路地为 \(s\) 以及 \(s\) 的反串建后缀数组并为 \(height\) 数组装上 \(st\) 表。

于是就可以 \(\Theta(1)\) 求任意两个前缀的最长公共后缀和任意两个后缀的最长公共前缀了。

---

这时候求 \(f_i\) 的 \(\Theta(n^2)\) 的做法（\(g_i\) 同）：

枚举 \(A\) 串长度 \(w\)，然后枚举 \(s\) 中的下标 \(l,r(r-l=w)\)。

如果两个后缀的最长公共前缀\(\ge w\)，则 \(f_{r+w-1}++\)。

如下图，三条黄线间的两个串组成 \(AA\) 串。

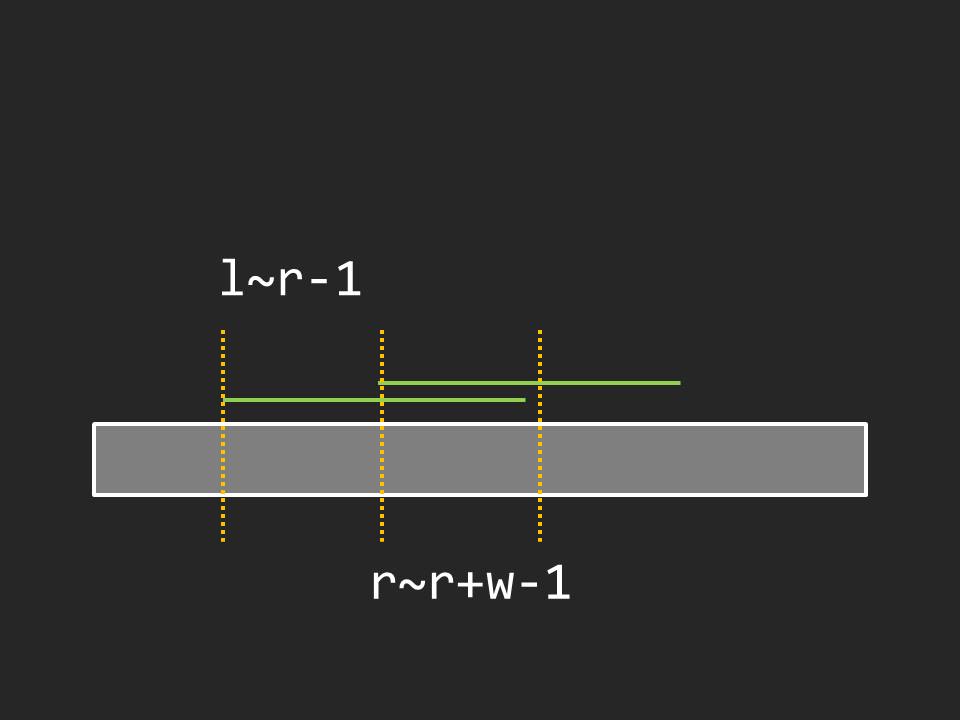
考虑一种套路优化（\(g_i\) 同）：

枚举了 \(w\) 以后任何相距 \(w\) 的下标是对应的。

所以可以在 \(w\) 倍数的下标设断点，此时一个 \(A\) 串至少要经过 \(1\) 个断点。

枚举相邻两个断点 \(l\) 和 \(r\)，求出它们的前缀最长公共后缀长度 \(lcs\) 和后缀最长公共前缀长度 \(lcp\) 之和 \(len\)：

表示经过两个断点且开头距离 \(w\) 的最长公共子串。

如果 \(len<w\)，说明没有同时经过这两个断点的 \(AA\) 串。

否则，\(f_{r+lcp-(lcp+lcs-1)\to r+lcp-1}++\)。

如下图，即两条紫线以及之间的子串为 \(AA\) 串：

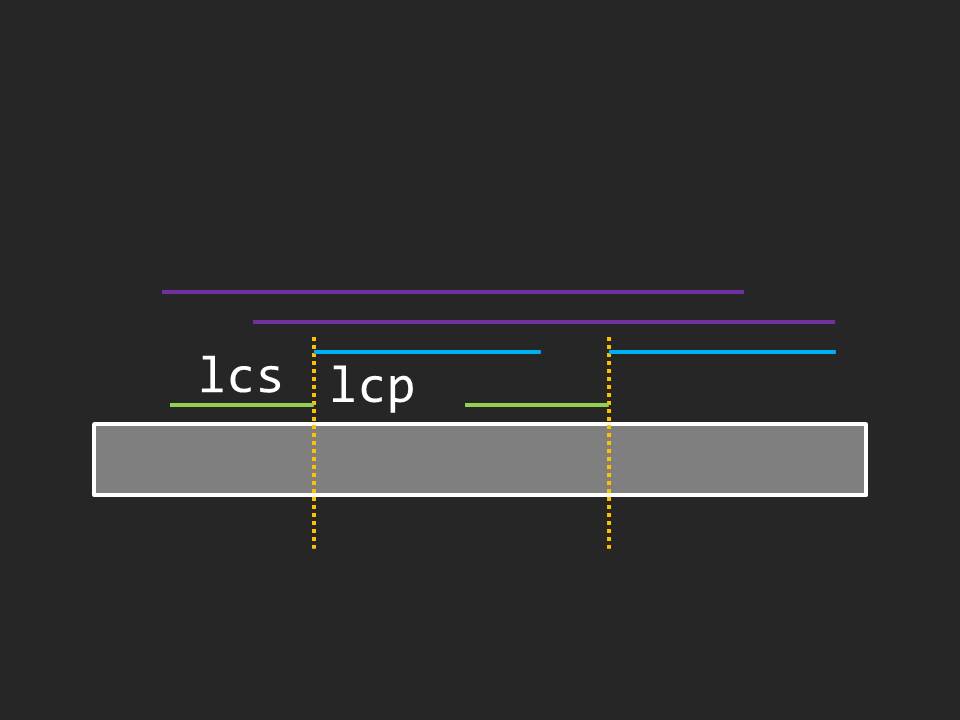
\(f_i,g_i\) 需要区间加，可以差分处理。

---

时间复杂度 \(\Theta(T\cdot n\log n)\)。

---

小蒟蒻讲不清楚，放代码吧：

#include <bits/stdc++.h>
using namespace std;

//Start
typedef long long ll;
typedef double db;
#define mp(a,b) make_pair(a,b)
#define x first
#define y second
#define b(a) a.begin()
#define e(a) a.end()
#define sz(a) int((a).size())
#define pb(a) push_back(a)
const int inf=0x3f3f3f3f;
const ll INF=0x3f3f3f3f3f3f3f3f;

//Data
const int N=3e4;
int n,f[N+7],g[N+7];

//SuffixArray
struct SuffixArray{
	char s[N+7];
	int m,c[N+7],tp[N+7],rk[N+7],sa[N+7];
	int h[N+7],st[N+7][20];
	void csort(){
		for(int i=0;i<=m;i++) c[i]=0;
		for(int i=1;i<=n;i++) c[rk[i]]++;
		for(int i=1;i<=m;i++) c[i]+=c[i-1];
		for(int i=n;i>=1;i--) sa[c[rk[tp[i]]]--]=tp[i];
	}
	void build(){
		memset(c,0,sizeof c);
		memset(tp,0,sizeof tp);
		memset(rk,0,sizeof rk);
		memset(sa,0,sizeof sa);
		memset(h,0,sizeof h);
		memset(st,0,sizeof st);
		for(int i=1;i<=n;i++) rk[i]=s[i],tp[i]=i;
		m=128,csort();
		for(int w=1,p=1,i;p<n;w<<=1,m=p){
			for(p=0,i=n-w+1;i<=n;i++) tp[++p]=i;
			for(i=1;i<=n;i++)if(sa[i]>w) tp[++p]=sa[i]-w;
			csort(),swap(rk,tp),rk[sa[1]]=p=1;
			for(i=2;i<=n;rk[sa[i]]=p,i++)
				if(tp[sa[i]]!=tp[sa[i-1]]||tp[sa[i]+w]!=tp[sa[i-1]+w]) p++;
		}
		for(int i=1,j,k=0;i<=n;h[rk[i++]]=k)
			for(k=k?k-1:k,j=sa[rk[i]-1];s[i+k]==s[j+k];k++);
		for(int i=1;i<=n;i++) st[i][0]=h[i];
		for(int w=1;w<=18;w++)
			for(int i=1;i+(1<<w)-1<=n;i++)
				st[i][w]=min(st[i][w-1],st[i+(1<<(w-1))][w-1]);
	}
	int Lcp(int a,int b){
		int l=rk[a],r=rk[b];
		if(l>r) swap(l,r); l++;
		int k=log2(r-l+1);
		return min(st[l][k],st[r-(1<<k)+1][k]);
	}
}a,b;

//KonnyWen
void KonnyWen(){
	memset(f,0,sizeof f);
	memset(g,0,sizeof g);
	scanf("%s",&a.s[1]),n=strlen(&a.s[1]);
	for(int i=1;i<=n;i++) b.s[i]=a.s[n+1-i];
	a.build(),b.build();
	for(int i=1;i<=n;i++) f[i]=g[i]=0;
	for(int w=1;w<=(n>>1);w++)
		for(int i=w;i<=n;i+=w){
			int l=i,r=i+w;
			int lcp=min(w,a.Lcp(l,r));
			int lcs=min(w-1,b.Lcp(n-(l-1)+1,n-(r-1)+1));
			if(lcp+lcs>=w){
				int cov=lcp+lcs-w+1;
				f[r+lcp-cov]++,f[r+lcp]--;
				g[l-lcs]++,g[l-lcs+cov]--;
			}
		}
	for(int i=1;i<=n;i++) f[i]+=f[i-1],g[i]+=g[i-1];
	ll ans=0;
	for(int i=1;i<n;i++) ans+=f[i]*g[i+1];
	printf("%lld\n",ans);
}

//Main
int main(){
	int t; scanf("%d",&t);
	while(t--) KonnyWen();
	return 0;
}

---

祝大家学习愉快！