cf437D The Child and Zoo

D. The Child and Zoo

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Of course our child likes walking in a zoo. The zoo has n areas, that are numbered from 1 to n.
The i-th area contains ai animals
in it. Also there are m roads in the zoo, and each road connects two distinct areas. Naturally the zoo is connected, so you can reach any area of the zoo
from any other area using the roads.

Our child is very smart. Imagine the child want to go from area p to area q.
Firstly he considers all the simple routes from p to q.
For each route the child writes down the number, that is equal to the minimum number of animals among the route areas. Let's denote the largest of the written numbers as f(p, q).
Finally, the child chooses one of the routes for which he writes down the value f(p, q).

After the child has visited the zoo, he thinks about the question: what is the average value of f(p, q) for all pairs p, q (p ≠ q)?
Can you answer his question?

Input

The first line contains two integers n and m (2 ≤ n ≤ 105; 0 ≤ m ≤ 105).
The second line contains n integers: a1, a2, ..., an (0 ≤ ai ≤ 105).
Then follow m lines, each line contains two integers xi and yi (1 ≤ xi, yi ≤ n; xi ≠ yi),
denoting the road between areas xi and yi.

All roads are bidirectional, each pair of areas is connected by at most one road.

Output

Output a real number — the value of .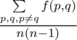

The answer will be considered correct if its relative or absolute error doesn't exceed 10 - 4.

Sample test(s)

input

4 3
10 20 30 40
1 3
2 3
4 3

output

16.666667

input

3 3
10 20 30
1 2
2 3
3 1

output

13.333333

input

7 8
40 20 10 30 20 50 40
1 2
2 3
3 4
4 5
5 6
6 7
1 4
5 7

output

18.571429

Note

Consider the first sample. There are 12 possible situations:

• p = 1, q = 3, f(p, q) = 10.
• p = 2, q = 3, f(p, q) = 20.
• p = 4, q = 3, f(p, q) = 30.
• p = 1, q = 2, f(p, q) = 10.
• p = 2, q = 4, f(p, q) = 20.
• p = 4, q = 1, f(p, q) = 10.

Another 6 cases are symmetrical to the above. The average is .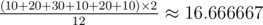

Consider the second sample. There are 6 possible situations:

• p = 1, q = 2, f(p, q) = 10.
• p = 2, q = 3, f(p, q) = 20.
• p = 1, q = 3, f(p, q) = 10.

Another 3 cases are symmetrical to the above. The average is .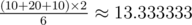

在鸿巨大的指导下才有了思路……orzlwh

首先把所有的点按权从大到小排序，然后顺序加入图中。对于一个新插入的点，可能有很多连出去的边，如果边的另一端已经在图中，就把它用并查集并起来，可以证明这些联通快之间的p就是新加入的点。然后统计答案。

黄巨大的题解：http://hzwer.com/3332.html

#include<iostream>
#include<cstdio>
#include<cstdlib>
#include<cmath>
#include<algorithm>
#include<cstring>
using namespace std;
struct sth
{
    int v,bh;
}p[100010];
int n,m;
int sz,to[200010],pre[200010],last[100010];
int fa[100010],sum[100010];
bool mark[100010];
double ans;
void Ins(int a,int b)
{
     sz++;to[sz]=b;pre[sz]=last[a];last[a]=sz;
}
inline bool comp(sth a,sth b)
{
     return a.v>b.v;
}
int getfa(int x)
{
    if(fa[x]==0) return x;
    return fa[x]=getfa(fa[x]);
}
int main()
{
    int i,j,x,y,a,b;
    scanf("%d%d",&n,&m);
    for(i=1;i<=n;i++)
    {
        scanf("%d",&p[i].v);
        p[i].bh=i;sum[i]=1;
    }
    for(i=1;i<=m;i++)
    {
        scanf("%d%d",&a,&b);
        Ins(a,b);Ins(b,a);
    }
    sort(p+1,p+1+n,comp);
    for(i=1;i<=n;i++)
    {
       x=p[i].bh;
       for(j=last[x];j;j=pre[j])
       if(mark[to[j]])
       {
          y=getfa(to[j]);
          a=getfa(x);
          if(a!=y)
          {
             ans+=(long long)sum[y]*sum[a]*p[i].v;
             sum[y]+=sum[a];
             fa[a]=y;
          }
       }
       mark[x]=1;
    }
    ans/=n*1.0;
    ans/=(n-1)*1.0;
    ans*=2.0;
    printf("%.12lf\n",ans);
    return 0;
}