HDU3863：No Gambling

Problem Description

One day, Flyvan introduced a new game to his two friends, Oregon Maple and Grape Skin. The game is quite simple. Given an N-sized grids, like the figure A shown below (as N = 4). The blue points are the places the first player can choose, and the red points are the places the second player can choose.

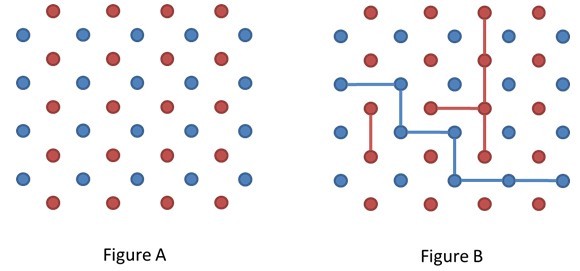
In the game, the two players take turns to choose two points to get connected by a stick. The two chosen points’ distance should be exactly one-unit length. The first player’s goal is to create a ‘bridge’ that connects a most left point and a most right point. The second player’s goal is to create a ‘bridge’ that connects a most top point and a most bottom point. Figure B shows a possible result (the first player won). In addition, the stick shouldn’t get crossed.

Now Flyvan will give the number N, and his two friends will play the game. Both of the two players will choose the best strategy. You can bet on one player, and if he wins the game, you’ll get twice money you bet~

Since you are a talented programmer, you surely won’t just do gambling. Please write a program to find out the player who you should bet on. As Oregon Maple is elder, he will always play first.

 

Input

Each line of the input is an integer N (2 <= N <= 270000), which indicated the number Flyvan chose. The end-of-file is denoted by a single line containing the number -1.

 

Output

If you think the first player will win, please output “I bet on Oregon Maple~”, else please output “I bet on Grape Skin~”.

 

Sample Input

2
-1

 

Sample Output

I bet on Oregon Maple~

第一个人从左到右连接蓝点

第二个人从上到下连接红点

轮流进行

看最后谁的线最多则赢

我们可以发现，只要是先手，那么连的线一定是最多了，因此代码也就只有短短的几行

#include <stdio.h>
int main()
{
    int n;
    while(scanf("%d",&n),n+1)
    puts("I bet on Oregon Maple~");
    return 0;
}