hihoCoder #1234 : Fractal（数学简单题）

时间限制:1000ms

单点时限:1000ms

内存限制:256MB

描述

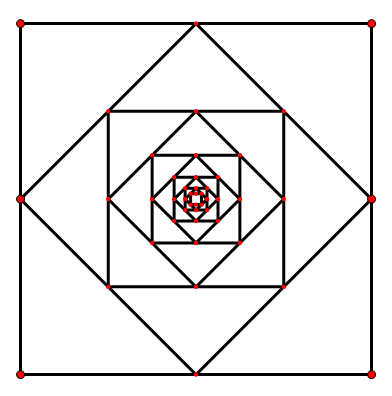
This is the logo of PKUACM 2016. More specifically, the logo is generated as follows:

1. Put four points A0(0,0), B0(0,1), C0(1,1), D0(1,0) on a cartesian coordinate system.

2. Link A0B0, B0C0, C0D0, D0A0 separately, forming square A0B0C0D0.

3. Assume we have already generated square AiBiCiDi, then square Ai+1Bi+1Ci+1Di+1 is generated by linking the midpoints of AiBi, BiCi, CiDi and DiAi successively.

4. Repeat step three 1000 times.

Now the designer decides to add a vertical line x=k to this logo( 0<= k < 0.5, and for k, there will be at most 8 digits after the decimal point). He wants to know the number of common points between the new line and the original logo.

输入

In the first line there’s an integer T( T < 10,000), indicating the number of test cases.

Then T lines follow, each describing a test case. Each line contains an float number k, meaning that you should calculate the number of common points between line x = k and the logo.

输出

For each test case, print a line containing one integer indicating the answer. If there are infinity common points, print -1.

样例输入

3
0.375
0.001
0.478

样例输出

-1
4
20

找出计算的规律即可

 #pragma comment(linker, "/STACK:1024000000,1024000000")
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<cmath>
 #include<math.h>
 #include<algorithm>
 #include<queue>
 #include<set>
 #include<bitset>
 #include<map>
 #include<vector>
 #include<stdlib.h>
 #include <stack>
 using namespace std;
 int dirx[]={,,-,};
 int diry[]={-,,,};
 #define PI acos(-1.0)
 #define max(a,b) (a) > (b) ? (a) : (b)
 #define min(a,b) (a) < (b) ? (a) : (b)
 #define ll long long
 #define eps 1e-10
 #define MOD 1000000007
 #define N 1000000
 #define inf 1e12
 double n;
 int num[];

 int main()
 {
     int t;
     scanf("%d",&t);
     while(t--){
         scanf("%lf",&n);
         int i;
         double x=;
         double y=0.5;
         for(i=;;i++){
             if(x>=n){
                 break;
             }
             x=x+y/2.0;
             y/=2.0;
         }
         int w=i;
         if(x==n){
             printf("-1\n");
         }
         else{
             int ans=;
             for(int i=;i<w;i++){
                 ans+=;
             }
             printf("%d\n",ans);
         }
     }
     return ;
 }