Max Sum(动态规划)

原创

---

http://acm.hdu.edu.cn/showproblem.php?pid=1003

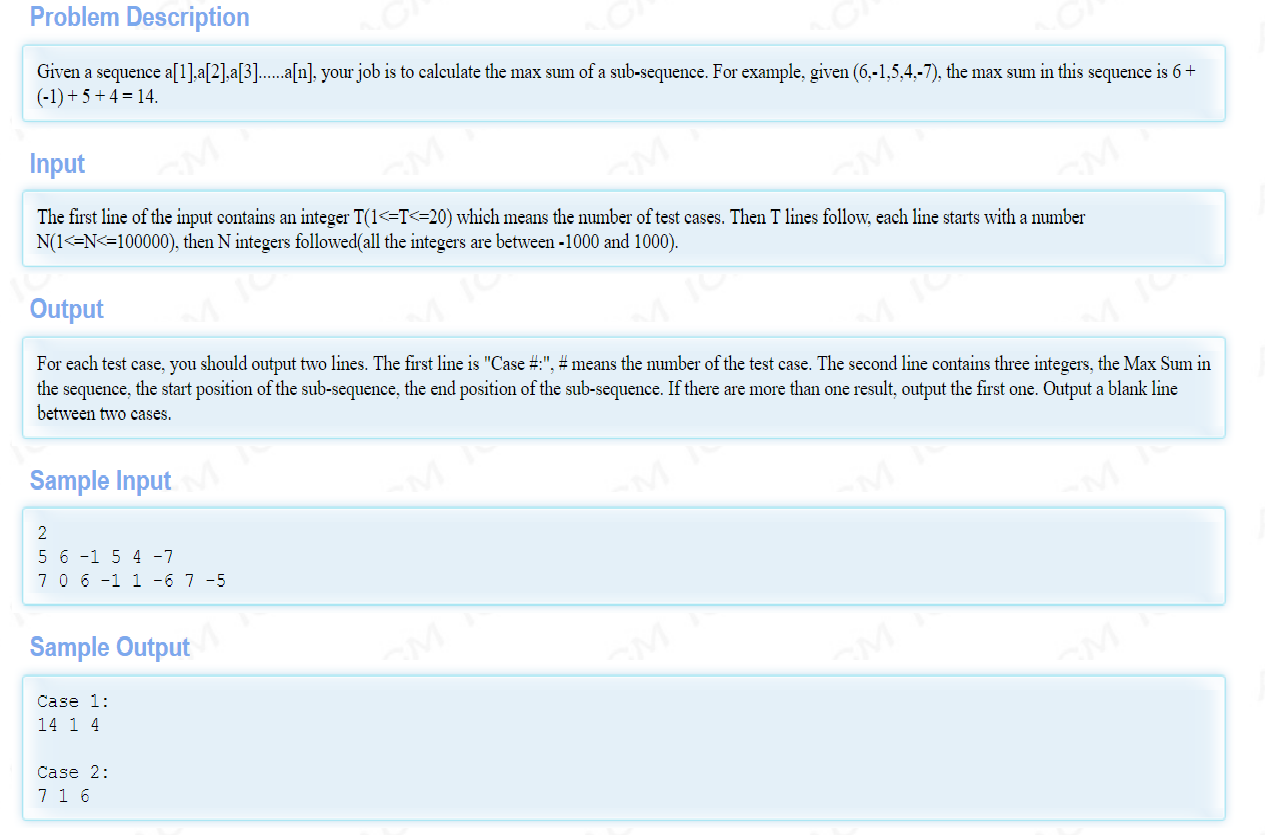
　　题目要求求出一个序列里面的最大序列和，序列要求是连续的，给出最大序列和，序列首元素下标和尾元素下标，按特定的格式输出。

　　解题思路：

　　　　动态规划，我们可以将所有序列按以序列中的元素a[i](i=1~n)结尾进行分类，比如：

　　　　以a[1]结尾的序列有：a[1]

　　　　以a[2]结尾的序列有：a[1]a[2],a[2]

　　　　以a[3]结尾的序列有：a[1]a[2]a[3],a[2][3],a[3]

　　　　...... 

　　　　这样所有序列都会包含在其中，一共被分为n大组，每大组里面包含许多小序列，从每大组里面选出最大的序列和，这样会选出n个

　　　　序列和，再从n个序列和中选出最大的就是题目要求的最大序列和了。

　　　　动态规划公式演算：

　　　　之前说过有n大组，用dp[]存储从每大组中选出来的最大序列和，其中

　　　　dp[1]=a[1]

　　　　dp[2]=max(a[1]a[2],a[2]),即从两个序列里面选出序列和最大的，既然只需要比较序列和，两个数比较大小，两个数同时减去一

　　　　个相同的数不影响比较，那么两个序列都先把元素a[2]减去，这样就成了dp[2]=max(dp[1]+a[2],a[2])。

　　　　dp[3]=max(a[1]a[2]a[3],a[2][3],a[3]),写成max(a[1]a[2]+a[3],a[2]+[3],0+a[3])更容易理解动态规划思想,3个序列都先把

　　　　a[3]提出变成max(a[1]a[2],a[2],0),再变成max(max(a[1]a[2],a[2]),0)，三个数比较，可以先比较其中2个，再和第三个比较，

　　　　可以发现max(a[1]a[2],a[2])就是dp[2]，所以max(a[1]a[2],a[2],0)就是max(dp[2],0),加回a[3]，max(dp[2]+a[3],a[3])。

　　　　所以我们可以轻而易举的按顺序求出n大组的序列和，然后再从n个序列和中求出最大的。

　　　　关于求最大序列和的首尾元素索引：

　　　　我们在求某个dp[i]的时候，代表目前是从以a[i]结尾的序列和中求出序列和最大的存入dp[i]中，所以尾元素可以得知。

　　　　尾元素得到，可以往回找到首元素。

Java AC

 import java.util.*;
 
 public class Main {
 
     public static void main(String[] args) {
         Scanner reader=new Scanner(System.in);
         int T=reader.nextInt();
         int count=1;
         while(T>0) {
             int N=reader.nextInt();
             int a[]=new int[N+1];
             for(int i=1;i<=N;i++) {
                 a[i]=reader.nextInt();
             }
             int dp=a[1];
             int sum_Max=dp;
             int start=1;
             int end=1;
             for(int i=2;i<=N;i++) {
                 dp=dp+a[i]>a[i]?(dp+a[i]):a[i];    //动态存储以a[1]~a[n]结尾的序列组的最大序列和
                 if(dp>sum_Max) {
                     sum_Max=dp;
                     end=i;    //结尾索引
                 }
             }
             //寻找开头索引
             int sum=0;
             for(int i=end;i>=1;i--) {
                 sum+=a[i];
                 if(sum==sum_Max) {
                     start=i;
                     //这里不能break,当序列中存在多个序列具有同样的最大序列和,题目要求输出第一个被找到的序列
                 }
             }
             System.out.println("Case "+count+":");
             System.out.println(sum_Max+" "+start+" "+end);
             if(T!=1) {
                 System.out.println();
             }
             T--;
             count++;
         }
     }
 
 }

21:21:39

2018-08-19