【noip2017】【Luogu3960】列队线段树

题目描述

Sylvia 是一个热爱学习的女♂孩子。

前段时间，Sylvia 参加了学校的军训。众所周知，军训的时候需要站方阵。

Sylvia 所在的方阵中有 n \times mn×m 名学生，方阵的行数为 nn ，列数为 mm 。

为了便于管理，教官在训练开始时，按照从前到后，从左到右的顺序给方阵中的学生从 1 到 n \times mn×m 编上了号码（参见后面的样例）。即：初始时，第 ii 行第 jj 列的学生的编号是 (i-1)\times m + j(i−1)×m+j 。

然而在练习方阵的时候，经常会有学生因为各种各样的事情需要离队。在一天中，一共发生了 qq 件这样的离队事件。每一次离队事件可以用数对 (x,y) (1 \le x \le n, 1 \le y \le m)(x,y)(1≤x≤n,1≤y≤m) 描述，表示第 xx 行第 yy 列的学生离队。

在有学生离队后，队伍中出现了一个空位。为了队伍的整齐，教官会依次下达这样的两条指令：

向左看齐。这时第一列保持不动，所有学生向左填补空缺。不难发现在这条指令之后，空位在第 xx 行第 mm列。
向前看齐。这时第一行保持不动，所有学生向前填补空缺。不难发现在这条指令之后，空位在第 nn 行第 mm列。

教官规定不能有两个或更多学生同时离队。即在前一个离队的学生归队之后，下一个学生才能离队。因此在每一个离队的学生要归队时，队伍中有且仅有第 nn 行第 mm 列一个空位，这时这个学生会自然地填补到这个位置。

因为站方阵真的很无聊，所以 Sylvia 想要计算每一次离队事件中，离队的同学的编号是多少。

注意：每一个同学的编号不会随着离队事件的发生而改变，在发生离队事件后方阵中同学的编号可能是乱序的。

输入输出格式

输入格式：

输入共 q+1q+1 行。

第 1 行包含 3 个用空格分隔的正整数 n, m, qn,m,q ，表示方阵大小是 nn 行 mm 列，一共发生了 qq 次事件。

接下来 qq 行按照事件发生顺序描述了 qq 件事件。每一行是两个整数 x, yx,y ，用一个空格分隔，表示这个离队事件中离队的学生当时排在第 xx 行第 yy 列。

输出格式：

按照事件输入的顺序，每一个事件输出一行一个整数，表示这个离队事件中离队学生的编号。

输入输出样例

输入样例#1：

输出样例#1：

说明

【输入输出样例 1 说明】

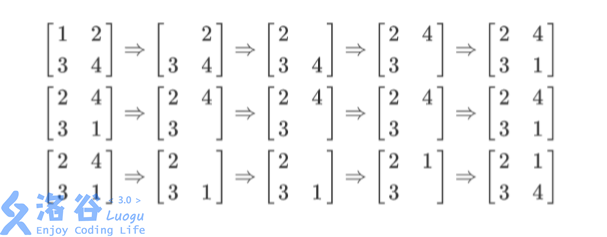
列队的过程如上图所示，每一行描述了一个事件。在第一个事件中，编号为 1 的同学离队，这时空位在第一行第一列。接着所有同学向左标齐，这时编号为 2 的同学向左移动一步，空位移动到第一行第二列。然后所有同学向上标齐，这时编号为 4 的同学向上一步，这时空位移动到第二行第二列。最后编号为 1 的同学返回填补到空位中。

【数据规模与约定】

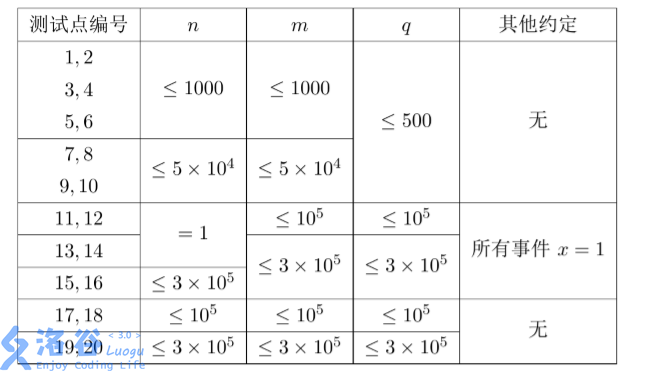
数据保证每一个事件满足 \(1 \le x \le n,1 \le y \le m1≤x≤n,1≤y≤m\)

前言

noip2017的时候我连线段树都不会，树状数组也只会板子，而且当时因为肛T2时间太多连50分都没写，30分就跑路了。现在回来看这个题，真的是一言难尽啊。

算法1

对于前50%的数据，我们取出所有询问用到的行和最后一列进行暴力模拟即可。

期望得分：50

算法2

对于11-16测试点，我们开1/2棵线段树，维护每个区间实际存在的数字个数，这样就可以利用区间长度-sum[x]的方法找到区间的第k个元素，同时我们维护1/2个vector，表示添加到末尾的数字，如果查找到的pos是在实际范围以内，那么直接按照pos计算，否则我们在vector中按照下标查找，之后再更新vector和线段树即可。

注意：线段树维护的是1~n+q/m+q的区间，所以空间记得开大一倍。

算法3

对每一行和最后一列维护n+1棵线段树和n+1个vector，由于动态开点我们的内存能够控制在\(nlogn\)的级别，vector中的元素在\(2q\)级别，不会超出内存限制，剩下的就按照算法2进行就行了，注意如果\(y=m\)，就不用对第x行的线段树进行操作了，否则我们就先在第x行找到答案，然后在第n+1棵线段树中找到第x个元素并添加到x中，然后把ans添加到n+1中。

算法3代码

其实这道题代码还是很好写的，35行，不到1K的长度。

#include <bits/stdc++.h>

#define ll long long

using namespace std;

int n,m,q,x,y,pos,tot,lim,rt[300005],ls[12000005],rs[12000005],sm[12000005];vector<ll>v[300005];

int que(int x,int l,int r,int v)

{

	if(l==r) return l;

	int mid=(l+r)>>1,tmp=mid-l+1-sm[ls[x]];

	if(v<=tmp) return que(ls[x],l,mid,v);

	return que(rs[x],mid+1,r,v-tmp);

}

void upd(int &x,int l,int r,int p)

{

	if(!x) x=++tot;sm[x]++;

	if(l==r) return;int mid=(l+r)>>1;

	if(p<=mid) upd(ls[x],l,mid,p);

	else upd(rs[x],mid+1,r,p);

}

ll wk1(int x,ll y)

{

	pos=que(rt[n+1],1,lim,x);upd(rt[n+1],1,lim,pos);

	ll ans=pos<=n?1ll*pos*m:v[n+1][pos-n-1];

	return v[n+1].push_back(y?y:ans),ans;

}

ll wk2(int x,int y)

{

	pos=que(rt[x],1,lim,y);upd(rt[x],1,lim,pos);

	ll ans=pos<m?1ll*(x-1)*m+pos:v[x][pos-m];

	return v[x].push_back(wk1(x,ans)),ans;

}

int main()

{

	scanf("%d%d%d",&n,&m,&q);lim=max(n,m)+q;

	for(;q--;printf("%lld\n",y==m?wk1(x,0):wk2(x,y))) scanf("%d%d",&x,&y);

}