Bell数和Stirling数

前面说到了Catalan数，现在来了一个Bell数和Stirling数。什么是Bell数，什么是Stirling数呢？两者的关系如何，有用于解决什么算法问题呢？

Bell数是以Bell这个人命名的，组合数学中的一组整数数列：B0=1,B1=1,B2=2,B3=5,B4=15,B5=52,B6=203....

Bn是基数为n的集合的划分方法数目。集合S的一个划分是定义为S的两两不相交的非空子集的族，他们的并是S。例如B3=5，集合S={1,2,3}的5中划分就是

{{1},{2},{3}}

{{1,2},{3}}

{{1,3},{2}}

{{2,3},{1}}

{{1,2,3}}.

计算Bn的递推公式是：

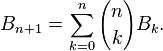
Stirling数有两类,第一类是有正负的，其绝对值是包含n个元素的集合分作K个环排列的方法数目。

递推公式为：

S(n,0)=0,S(n,1)=1.

S(n+1,k)=S(n,k-1)+nS(n,k)

第二类Stirling数S(n,k)是把基数为n的集合划分为正好K个非空集的方法的数目。也就是把标记为1,2,3...n的几个小球放到k个盒子里面，每个盒子不空，所有排放的方法数。

递推公式为：

S(n,n+1)=0

S(n,0)=0

S(0,0)=1

S(n,m)=mS(n-1,m)+S(n-1,m-1)

这个可以这样理解。把n个数划分为m份，如果已经有了n-1的划分的话，可以通过在S(n-1,m)的m个划分子集中中加入第n个元素从而构成S(n,m)，也可以通过在S(n-1,m-1)再加入一个独立的子集{n}构成S(n,m).

Bell数与第二类Stirling数有如下关系：

B(n)=

这个很好理解。