线段拟合(带拉格朗日乘子,HGL)
线段特征上的扫描点满足 (1)。本文的线段特征定义为:L: [dL, φL, PLs, PLe]T,如图1所示。其中,dL为笛卡尔坐标系中原点(激光传感器所在位置)到线段的距离, φL为线段特征的倾角,PLs为线段特征起点,PLe为线段特征终点。线段特征在笛卡尔坐标系下方程为:
 (1)
(1)
其中,dL > 0,-π < φL < π,xi = ρicosφi,yi = ρisinφi。
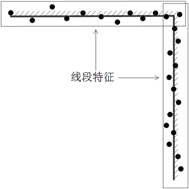
图1 线段
前几节中,通过统计学方法划分出若干区域,为了准确提取线段特征,采用带约束的最小二乘法对每个划分区域特征进行特征提取,将(1)式转换为如下形式:
 (2)
(2)
式中 S、E——线段端点。
将上式改写为矩阵形式有:
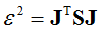 (3)
(3)
其中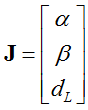 ,
,  ,
,  ,
,  。由于α2+β2=1,引入拉格朗日乘子λ,得:
。由于α2+β2=1,引入拉格朗日乘子λ,得:
 (4)
(4)
其中,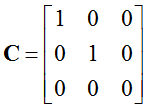 ,满足JTCJ=1。令
,满足JTCJ=1。令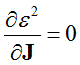 ,得:
,得:
 (5)
(5)
解上式的广义特征值与广义特征向量,S为一个正定矩阵,待求特征向量J一定对应最小的特征值λ。当α与β确定以后,可以求得:
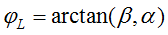 (6)
(6)
然后,求出线段特征dL。最后,转换到全局坐标系下。
文献[1]给出了一种误差传播方法,通过最小化隐含的关系方程F(I,O),给出最终误差(I输入误差,O输出误差)。将误差扩展到协方差矩阵,可以通过输入的协方差矩阵ΣI,得到输出的协方差矩阵ΣL。则有:
 (7)
(7)
其中, 。
。 ,
,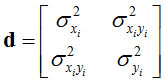 令:
令:
 (8)
(8)
代入最后计算出ΣL。
[1] Haralick R M. Propagating covariance in computer vision[M]. Performance Characterization in Computer Vision. Springer Netherlands, 2000: 95-114.
线段拟合(带拉格朗日乘子,HGL)的更多相关文章
- 关于拉格朗日乘子法和KKT条件
解密SVM系列(一):关于拉格朗日乘子法和KKT条件 标签: svm算法支持向量机 2015-08-17 18:53 1214人阅读 评论(0) 收藏 举报 分类: 模式识别&机器学习(42 ...
- 装载:关于拉格朗日乘子法与KKT条件
作者:@wzyer 拉格朗日乘子法无疑是最优化理论中最重要的一个方法.但是现在网上并没有很好的完整介绍整个方法的文章.我这里尝试详细介绍一下这方面的有关问题,插入自己的一些理解,希望能够对大家有帮助. ...
- 约束优化方法之拉格朗日乘子法与KKT条件
引言 本篇文章将详解带有约束条件的最优化问题,约束条件分为等式约束与不等式约束,对于等式约束的优化问题,可以直接应用拉格朗日乘子法去求取最优值:对于含有不等式约束的优化问题,可以转化为在满足 KKT ...
- 机器学习笔记——拉格朗日乘子法和KKT条件
拉格朗日乘子法是一种寻找多元函数在一组约束下的极值方法,通过引入拉格朗日乘子,可将有m个变量和n个约束条件的最优化问题转化为具有m+n个变量的无约束优化问题.在介绍拉格朗日乘子法之前,先简要的介绍一些 ...
- 真正理解拉格朗日乘子法和 KKT 条件
这篇博文中直观上讲解了拉格朗日乘子法和 KKT 条件,对偶问题等内容. 首先从无约束的优化问题讲起,一般就是要使一个表达式取到最小值: \[min \quad f(x)\] 如 ...
- 关于拉格朗日乘子法与KKT条件
关于拉格朗日乘子法与KKT条件 关于拉格朗日乘子法与KKT条件 目录 拉格朗日乘子法的数学基础 共轭函数 拉格朗日函数 拉格朗日对偶函数 目标函数最优值的下界 拉格朗日对偶函数与共轭函数的联系 拉 ...
- 拉格朗日乘子法 - KKT条件 - 对偶问题
接下来准备写支持向量机,然而支持向量机和其他算法相比牵涉较多的数学知识,其中首当其冲的就是标题中的拉格朗日乘子法.KKT条件和对偶问题,所以本篇先作个铺垫. 大部分机器学习算法最后都可归结为最优化问题 ...
- 支持向量机(SVM)必备概念(凸集和凸函数,凸优化问题,软间隔,核函数,拉格朗日乘子法,对偶问题,slater条件、KKT条件)
SVM目前被认为是最好的现成的分类器,SVM整个原理的推导过程也很是复杂啊,其中涉及到很多概念,如:凸集和凸函数,凸优化问题,软间隔,核函数,拉格朗日乘子法,对偶问题,slater条件.KKT条件还有 ...
- 机器学习——支持向量机(SVM)之拉格朗日乘子法,KKT条件以及简化版SMO算法分析
SVM有很多实现,现在只关注其中最流行的一种实现,即序列最小优化(Sequential Minimal Optimization,SMO)算法,然后介绍如何使用一种核函数(kernel)的方式将SVM ...
随机推荐
- JS及Dom练习 | 模态对话框及复选框操作
<!DOCTYPE html> <html lang="en"> <head> <meta charset="UTF-8&quo ...
- jquery 添加关键字小插件
模块化封装,兼容seajs /** * User: c3t * Date: 14-3-25 * Time: 下午4:16 */ define(function (require, exports, m ...
- Linux Kernel文件系统写I/O流程代码分析(一)
Linux Kernel文件系统写I/O流程代码分析(一) 在Linux VFS机制简析(二)这篇博客上介绍了struct address_space_operations里底层文件系统需要实现的操作 ...
- javascript数组与字符串之间转换
一.数组转字符串(将数组元素用某个字符连接成字符串) var a, b;a = new Array(0,1,2,3,4);b = a.join("-"); 二.字符串转数组(将字符 ...
- .net mvc 设置div的动态部分视图内容 dynamic partial view
示例效果:点击按钮,在div中 显示不同的partial view的内容 $("#btnEdit").click(function () { //动态获取相应的部分视图 var u ...
- Mac 10.11.4 安装mysql-5.7.13 默认密码问题
今天下载了一个最新版的mysql dmg安装包来安装mysql,安装的整个过程竟然都没有提示输入root用户默认密码,我也没太在意,然后连接数据库时竟然提示输入密码,当时就一脸懵逼了.尝试各种密码,为 ...
- java参数传递之值传递
一 概述 1.什么是参数传递? 调用方法时向形参传递数据的过程叫做参数传递.在编程语言中有两种传递方式:值传递与引用传递.必须强调的是,这里提到的两种传递方式不是仅限于java使用到的传递方式,而是出 ...
- json中定义数组
我们经常会看到在js中定义普通函数: function f1(a,b){ console.log(a+b); } f1(); 今天我们看一下如何在json里边定义函数并调用: var json = { ...
- wxpython 设置鼠标样式
鼠标指针被设置为放大镜样式.可用的鼠标指针样式有: wx.CURSOR_ARROWwx.CURSOR_RIGHT_ARROWwx.CURSOR_BLANKwx.CURSOR_BULLSEYEwx.CU ...
- matlab练习程序(随机粒子切换特效)
视频制作软件中一般都会有相邻帧切换的特效,我过去用过vagas好像就有很多切换特效. 我想这个也算是其中一种吧,虽然我不确定实际中到底有没有这种切换. 实际上我只是下班后太无聊了,写着玩的,没什么高深 ...
