图论---图的m-点着色判定问题(回溯法--迭代式)

转自

图的m着色问题

图的m-着色判定问题——给定无向连通图G和m种不同的颜色。用这些颜色为图G的各顶点着色，每个顶点着一种颜色，是否有一种着色法使G中任意相邻的2个顶点着不同颜色?

图的m-着色优化问题——若一个图最少需要m种颜色才能使图中任意相邻的2个顶点着不同颜色，则称这个数m为该图的色数。求一个图的最小色数m的问题称为m-着色优化问题。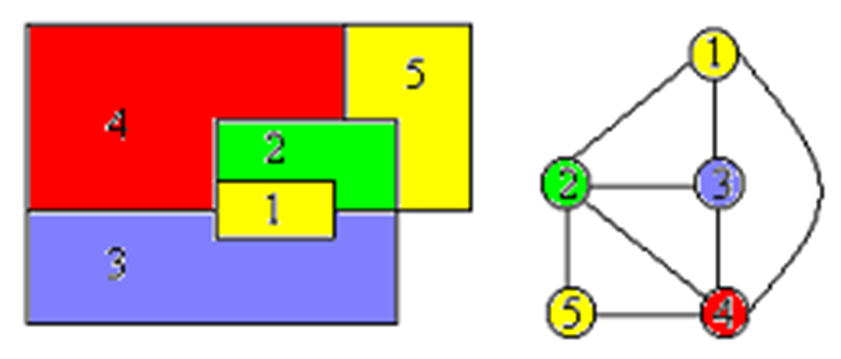

算法描述（迭代算法）

color[n]存储n个顶点的着色方案，可以选择的颜色为1到m

t=1->n

对当前第t个顶点开始着色：

　if: 　　t>n  则已求得一个解，输出着色方案即可

else: 　　依次对顶点t着色1-m，

　　　  　　if: 　　t与所有其它相邻顶点无颜色冲突，则继续为下一顶点着色；

　　　　　 else:  　  回溯，测试下一颜色。

///图着色问题回溯法
/**
无向图邻接矩阵示例
1 1 0 0 0
1 1 0 1 0
1 0 0 1 0
1 0 0 1 0
1 1 1 0 0
*/

#include "cstdio"
#include "cstring"
int color[];
bool ok(int k,int c[][])
{
    for(int i=;i<k;i++)
    {
        if(c[k][i]==&&color[i]==color[k])///看已经着色的 与之相连的顶点和他同色与否？
            return false;
    }
    return true;
}
int graphColor(int n,int m,int c[][])
{
    int cnt=;
    memset(color,,sizeof(color));
    int k=;
    while(k>=)
    {
        color[k]+=;///染第一种颜色
        while(color[k]<=m)
        {
            if(ok(k,c))
                break;
            else
                color[k]++;///搜索下一个颜色
        }///挑选合适颜色
        if(color[k]<=m&&k==n)///找完  输出
        {
            for(int i=;i<=n;i++)
                printf("%d ",color[i]);
            printf("\n");
            cnt++;
        }
        else if(color[k]<=m&&k<n)
        {
            k++;///染下一个顶点
        }
        else
        {
            color[k]=;///回溯 找其他方法
            k--;
        }
    }
    return cnt;
}
int main()
{
    int n,m,i,j;
    int c[][];
    printf("输入顶点数n和着色数m:\n");
    scanf("%d %d",&n,&m);
    printf("输入无向图的邻接矩阵:\n");
    for(i=;i<=n;i++)
        for(j=;j<=n;j++)
            scanf("%d",&c[i][j]);
    printf("着色所有可能的解:\n");
    int cnt=graphColor(n,m,c);
    printf("方案数: %d\n",cnt);
}

每一个程序，都在讲着自己的故事

写程序 讲故事