NOIP2016愤怒的小鸟 [状压dp]

愤怒的小鸟

题目描述

Kiana 最近沉迷于一款神奇的游戏无法自拔。

简单来说，这款游戏是在一个平面上进行的。

有一架弹弓位于 (0,0) 处，每次 Kiana 可以用它向第一象限发射一只红色的小鸟，小鸟们的飞行轨迹均为形如 y=ax^2+bx的曲线，其中 a,b是Kiana 指定的参数，且必须满足 a<0,a,b 都是实数。

当小鸟落回地面（即 x 轴）时，它就会瞬间消失。

在游戏的某个关卡里，平面的第一象限中有 n 只绿色的小猪，其中第 i 只小猪所在的坐标为 (xi​,yi​) 。

如果某只小鸟的飞行轨迹经过了 (xi​,yi​) ，那么第 i 只小猪就会被消灭掉，同时小鸟将会沿着原先的轨迹继续飞行；

如果一只小鸟的飞行轨迹没有经过 (xi​,yi​) ，那么这只小鸟飞行的全过程就不会对第 i 只小猪产生任何影响。

例如，若两只小猪分别位于 (1,3) 和 (3,3) ，Kiana 可以选择发射一只飞行轨迹为 y=-x^2+4x 的小鸟，这样两只小猪就会被这只小鸟一起消灭。

而这个游戏的目的，就是通过发射小鸟消灭所有的小猪。

这款神奇游戏的每个关卡对 Kiana来说都很难，所以Kiana还输入了一些神秘的指令，使得自己能更轻松地完成这个游戏。这些指令将在【输入格式】中详述。

假设这款游戏一共有 T 个关卡，现在 Kiana想知道，对于每一个关卡，至少需要发射多少只小鸟才能消灭所有的小猪。由于她不会算，所以希望由你告诉她。

输入输出格式

输入格式：

第一行包含一个正整数 T ，表示游戏的关卡总数。

下面依次输入这 T 个关卡的信息。每个关卡第一行包含两个非负整数 n,mn,m ，分别表示该关卡中的小猪数量和 Kiana 输入的神秘指令类型。接下来的 n 行中，第 ii 行包含两个正实数 xi​,yi​ ，表示第 i 只小猪坐标为 (xi​,yi​)。数据保证同一个关卡中不存在两只坐标完全相同的小猪。

如果 m=0 ，表示Kiana输入了一个没有任何作用的指令。

如果 m=1 ，则这个关卡将会满足：至多用 ⌈n/3+1⌉ 只小鸟即可消灭所有小猪。

如果 m=2 ，则这个关卡将会满足：一定存在一种最优解，其中有一只小鸟消灭了至少 ⌊n/3⌋ 只小猪。

保证 1≤n≤18 ， 0≤m≤2 ， 0<xi​,yi​<10 ，输入中的实数均保留到小数点后两位。

上文中，符号 ⌈c⌉ 和 ⌊c⌋ 分别表示对 c 向上取整和向下取整，例如： ⌈2.1⌉=⌈2.9⌉=⌈3.0⌉=⌊3.0⌋=⌊3.1⌋=⌊3.9⌋=3 。

输出格式：

对每个关卡依次输出一行答案。

输出的每一行包含一个正整数，表示相应的关卡中，消灭所有小猪最少需要的小鸟数量。

输入输出样例

输入样例#1：

2

2 0

1.00 3.00

3.00 3.00

5 2

1.00 5.00

2.00 8.00

3.00 9.00

4.00 8.00

5.00 5.00

输出样例#1：

1

1

输入样例#2：

3

2 0

1.41 2.00

1.73 3.00

3 0

1.11 1.41

2.34 1.79

2.98 1.49

5 0

2.72 2.72

2.72 3.14

3.14 2.72

3.14 3.14

5.00 5.00

输出样例#2：

2

2

3

输入样例#3：

1

10 0

7.16 6.28

2.02 0.38

8.33 7.78

7.68 2.09

7.46 7.86

5.77 7.44

8.24 6.72

4.42 5.11

5.42 7.79

8.15 4.99

输出样例#3：

6

说明

【样例解释1】

这组数据中一共有两个关卡。

第一个关卡与【问题描述】中的情形相同,2只小猪分别位于 (1.00,3.00) 和 (3.00,3.00) ，只需发射一只飞行轨迹为 y = -x^2 + 4x 的小鸟即可消灭它们。

第二个关卡中有 5 只小猪，但经过观察我们可以发现它们的坐标都在抛物线 y = -x^2 + 6x 上，故Kiana只需要发射一只小鸟即可消灭所有小猪。

【数据范围】

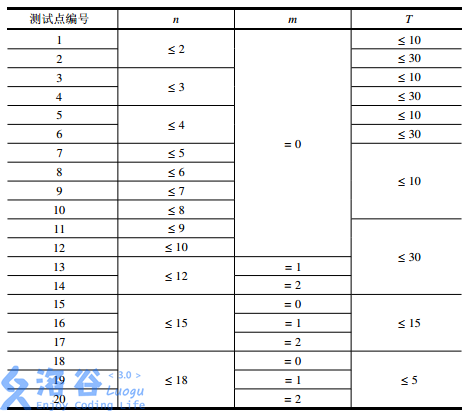
题解

这道题有三种做法:强力剪枝搜索,记忆化搜索,状压dp,这里主要讲状压dp的做法

题目要求我们用最少的小鸟击落所有的猪,而小鸟的运动轨迹是一条抛物线,那么我们就想可不可以枚举两个不同的小鸟来来确定这条抛物线呢?这是肯定的,因为这条抛物线只有两个参数a,b,我们将两个小鸟的坐标带入进去就可以求得这两个参数,解二元一次方程,这应该是初中数学内容

\(a*x_1^2+b*x_1=y_1\)

\(a*x_2^2+b*x_2=y_2\)

得到

\(a=(x_2*y_1-x_1*y_2)/(x_1^2*x_2-x_2^2*x_1);\)

\(b=(x_1^2*y_2-x_2^2*y_1)/(x_1^2*x_2-x_2^2*x_1);\)

然后要注意\(x_1^2*x_2-x_2^2*x_1!=0\),即分母不能为0

求出这条抛物线后,我们就可以预处理这条抛物线打下了哪些猪,可以用一个二位数组f[i][j]保存通过枚举i和j这两个猪所构成的抛物线打下了哪些猪

注意:题目要求a<0,所以碰到a>0的情况就要舍去,fabs是取浮点数的绝对值,虽然abs也可用但是慢很多

然后就是标准的状压dp,状态转移方程为dp[sta|f[i][j]]=min(dp[sta|f[i][j]],dp[sta]+1),这里的f[i][j]指的是是合法的抛物线

#include<bits/stdc++.h>
#define rg register
#define il inline
#define Min(a,b) (a)<(b)?(a):(b)
#define Max(a,b) (a)>(b)?(a):(b)
#define lol long long
using namespace std;

const int N=20;
const double eps=1e-10;

void in(int &ans) {
	ans=0; int f=1; char i=getchar();
	while(i<'0' || i>'9') {if(i=='-') f=-1; i=getchar();}
	while(i>='0' && i<='9') ans=(ans<<1)+(ans<<3)+i-'0',i=getchar();
	ans*=f;
}

int T,n,m;
double a,b,x[N],y[N];
int dp[1<<18],s[N][N];

il void clear() {
    a=b=0;
    memset(dp,0x3f,sizeof(dp));
    memset(s,0,sizeof(s));
}

bool check(int i,int j) {
    if(fabs((x[j]-x[i])/(x[i]*x[j]))<=eps) return 0;
    a=(x[i]*y[j]-x[j]*y[i])/(x[j]-x[i])/(x[i]*x[j]);
    b=(x[i]*x[i]*y[j]-x[j]*x[j]*y[i])/(x[i]*x[i]*x[j]-x[j]*x[j]*x[i]);
    return (a<0);
}

void read() {
    in(n),in(m);
    for(rg int i=1;i<=n;i++)
        scanf("%lf%lf",&x[i],&y[i]);
}

void work() {
    for(rg int i=1;i<=n;i++) {
        for(rg int j=1;j<=n;j++) {
            if(fabs(x[i]-x[j])<=eps) continue;
            if(!check(i,j)) continue;
            s[i][j]|=(1<<i-1)|(1<<j-1);
            for(rg int k=1;k<=n;k++) {
                if(i==k || j==k) continue;
                if(fabs(a*x[k]*x[k]+b*x[k]-y[k])<=eps) s[i][j]|=1<<k-1;
            }
        }
    }
}

void DP() {
    int tot=1<<n; dp[0]=0;
    for(rg int sta=0;sta<tot;sta++) {
        for(rg int i=1;i<=n;i++) {
            if(sta&(1<<i-1)) continue;
            for(rg int j=1;j<=n;j++) {
                if(!s[i][j]) continue;
                if(sta&(1<<j-1)) continue;
                if(fabs(x[i]-x[j])<=eps) continue;
                dp[sta|s[i][j]]=Min(dp[sta|s[i][j]],dp[sta]+1);
            }
            dp[sta|(1<<i-1)]=Min(dp[sta|(1<<i-1)],dp[sta]+1);
        }
    }
    printf("%d\n",dp[(1<<n)-1]);
}

int main()
{
    in(T);
    while(T--) {
        clear(),read();
        work(),DP();
    }
    return 0;
}