树上两点的最近公共祖先问题(Least Common Ancestors)

概念:

　　对于有根树T的两个节点u,v,最近公共祖先LCA(T, u, v)表示一个节点 x, 满足 x 是 u , v 的祖先且 x 的深度尽可能的大.即从 u 到 v 的路径一定经过点 x.

算法:

　　解决LCA问题比较经典的是Tarjan - LCA 离线算法,还有另外一种方法,是经过一系列处理将LCA问题转化为和数据结构有关的RMQ问题加以解决.这里只阐述下Tarjan - LCA 算法.

Tarjan - LCA算法:

　　此算法基于 DFS 框架,每搜到一个新的节点,就创建由这个节点构成的集合,再对当前节点的每个子树进行搜索,回溯时把当前点并入到上一个点所在的集合之中,每回溯一个点,关于这个点与已被访问过的所有点的询问就会得到解决.如果有一个从当前点到节点 v 的询问,且 v 已被访问过,那么这两点的最近公共祖先一定是 v 所在集合的代表．

伪代码:

　　对于每一点 u：

　　１:建立以 u 为代表的集合;

　　2:依次遍历与 u 相连的每个节点 v,如果 v 没有被访问过,那么对 v 使用Tarjan - LCA 算法,结束后,将 v 的集合并入 u 的集合.

　　3:对于 u 有关的询问(u, v),如果 v 被访问过,则结果就是v 所在的集合的代表元素.

实现上关于集合的查找和合并用并查集实现,存图用的链式前向星.

用图来描述下:

初始化图:

为了方便描述,A ~ H 映射为 1 ～ 8了.图中灰色的点“代表未被访问的点”; 绿色的点代表 “正在访问的点”, 即还在执行LCA算法未结束的点; 红色的点代表“已经被访问过的点”,即 彻底完成Tarjan - LCA算法的点.注意这个算法是递归的,即同时存在多个正在访问的点.

第一步:从根节点开始访问,访问 A 节点,并构造以 A 节点构成的集合.完成后节点的状态如图所示:

且此时pre数组的值为:(pre数组为并查集的数组,pre[i] = j 代表 i 的祖先为 j)

pre   0    1    2    3    4    5    6    7    8

-1   1   -1   -1   -1   -1   -1   -1   -1

(A节点未处理结束........)

第二步:访问 B 节点,并创建由 B 节点构成的集合,完成此步之后图的状态如图所示:

此时的pre数组为:

pre   0    1    2    3    4    5    6    7    8

-1   1    2   -1   -1   -1   -1   -1   -1

(B节点未处理结束........)

第三步选择第一个与 B 节点相连的 C 节点,访问之,并同样创建以其为代表的集合:

此时的pre数组为:

pre   0    1    2    3    4    5    6    7    8

-1   1    2    3   -1   -1   -1   -1   -1

(C节点未处理结束........)

第四步访问第一个与 C 节点相连的节点 E,创建由 E 节点构成的集合,此时pre数组和图的状态为:

pre   0    1    2    3    4    5    6    7    8

-1   1    2    3   -1    5   -1   -1   -1

此时由于 E 号节点没有了子节点,于是开始处理关于 E 号节点的查询,这里为了方便观察,用二维数组lca[i][j] 来表示 LCA(i, j)了.因为这里的 A, B, C, 三个节点已被访问过,所以可以计算出关于 E 节点的部分查询:(关于(E, v)的查询为  v 节点所在集合的祖先,即pre[v])

lca     1    2    3    4    5    6    7    8

5(E)   1    2    3   -1   -1   -1   -1   -1

此时关于 E  号节点的处理就已经全部完成,由 E 回溯到 C, 并把 E 加入到 C 所在的集合,即执行 pre[5] = find(pre[3]), 之后pre[5] == 3.

第五步:访问第二个与 C 节点相连的节点 F,做相同的操作,pre数组以及图此时的状态:

pre   0    1    2    3    4    5    6    7    8

-1   1    2    3   -1    3    6   -1   -1

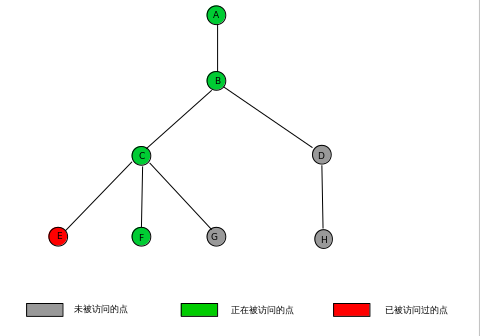
同样由于 F 节点也没有了子节点,处理关于 F 节点的查询,这里被访问过得节点有 A, B, C, E,对其采用算法的 "3 步骤"之后:

lca     1    2    3    4    5    6    7    8

6(F)   1    2    3   -1   3   -1   -1   -1

此时关于 F 节点的有关操作就结束了,同样回溯到 C 节点,也就是步骤三,下一步将访问最后一个与 C 节点相邻的节点 G,回溯到 C之后,把 F 点合并到 C所在的集合, 即 pre[6] = find(pre[3]), pre[6] = 3.

第六步:访问节点 G,之后的pre数组以及图为:

pre   0    1    2    3    4    5    6    7    8

-1   1    2    3   -1    3    3    7   -1

可以看到也没有了子节点,那么同上,做出相同的操作:

lca     1    2    3    4    5    6    7    8

7(G)   1    2    3   -1   3    3   -1   -1

此时关于 G 节点的处理也结束了,回溯到 C, 并且把 G 节点并入到集合 C. pre[7] = find(pre[c]), pre[7] = 3;

(此时由于已经没有了和 C 相邻的节点,那么接下来就要会到第三步)

第三步:此时 C 节点的所有子树都访问完毕,pre数组和图为:

pre   0    1    2    3    4    5    6    7    8

-1   1    2    3   -1    3    3    3   -1

访问的 C 节点此时也没有了相邻节点,那么对于 C 节点的所有处理即将也要完成,对节点C 执行算法的第三步得:

lca     1    2    3    4    5    6    7    8

3(C)   1    2    3   -1   3    3     3   -1

执行完毕后,继续回溯到上一节点 B,并把集合 C 和集合 B合并,pre[3] = find(pre[2]), pre[3] = 2.

(此时第三步运行完毕,将返回第二步.)

第七步:访问第二个 B 节点的子节点 D,构造由 D 构成的集合.此时pre数组以及图的状态为:

pre   0    1    2    3    4    5    6    7    8

-1   1    2    2    4    2    2    2  -1

(由于D节点还有子节点,那么继续下一步,此时第七步还未完成......)

第八步:访问与 D 节点的子节点 H,此时pre数组以及图的状态为:

pre   0    1    2    3    4    5    6    7    8

-1   1    2    2    4    2    2    2   8

此时由于 H 节点已经没有了子节点,那么就该处理关于 H 节点的询问了,处理完成后lca数组如下:

lca     1    2    3    4    5    6    7    8

8(H)   1    2    2    4   2    2     2   -1

之后再回溯到 D 节点,并且把自己并入到 D 节点所在的集合.

(此时第八步运行结束,将返回到第七步)

第七步:此时正处于访问节点 D 的状态此时pre数组以及图的状态为:

pre   0    1    2    3    4    5    6    7    8

-1   1    2    2    4    2    2    2    4

紧接着,由于 D 节点的所有相邻节点已经访问完毕,那么此时就需要处理关于 D 节点的询问并回溯到 B 节点,并把 D 所在的集合和 B 所在的集合合并,pre[4] = find(pre[2]), pre[4]=2.

lca     1    2    3    4    5    6    7    8

4(D)   1    2    2    4   2    2     2   4

(此时第七步完成,将返回到第二步)

第二步:

同理,B 节点的所有子节点在此时也全部访问完毕,此时的pre数组以及图的状态为:

pre   0    1    2    3    4    5    6    7    8

-1   1    2    2    2    2    2    2    2

此时处理关于 B,点的询问,处理完成后回溯到 A 节点,回溯之后把 B 所在的集合并入到A所在的集合.

lca     1    2    3    4    5    6    7    8

2(B)   1    2    2    2    2    2     2   2

(此时第二步也全部完毕,即将回溯到第一步)

第一步:此时pre数组以及图的状态为:

pre   0    1    2    3    4    5    6    7    8

-1   1    1    1    1    1    1    1    1

处理关于A节点所有查询,结束整个算法:

lca     1    2    3    4    5    6    7    8

1(A)   1    1    1    1    1    1    1    1

最终的pre数组, lca数组, 图的状态:

pre   0    1    2    3    4    5    6    7    8

-1   1    1    1    1    1    1    1    1

lca     1    2    3    4    5    6    7    8

1(A)   1    1    1    1    1    1    1    1

2(B)   1    2    2    2    2    2     2   2

3(C)   1    2    3   -1    3    3     3   -1

4(D)   1    2    2    4    2    2     2    4

5(E)   1     2    3   -1   5    -1   -1   -1

6(F)   1     2    3   -1    3    6    -1   -1

7(G)   1    2    3   -1    3    3    7    -1

8(H)   1    2    2    4    2    2     2    8

由于LCA(u, v) = LCA(v, u)，所以上图再经过调整就可以得出所有询问了.

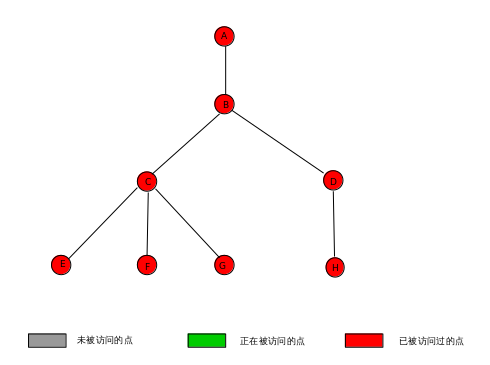
至此,Tarjan - LCA算法就用图描述完毕了.

代码：

//说明:使用链式前向星存图和所有询问,head[]和edge[]表示图, qhead[]和qedge[]表示询问.由于链式前向星只能存储有向边,那么对于无向图的树来说,每条边要存储两次.对于集合的操作用并查集来完成.

 #include <bits/stdc++.h>

 const int maxn = ;
 int pre[maxn];
 int head[maxn];
 int qhead[maxn];

 struct NODE {int to;int next;int lca;};
 NODE edge[maxn];
 NODE qedge[maxn];

 int Find(int x) { return x == pre[x] ? x : pre[x] = Find(pre[x]);}//并查集

 bool visit[maxn];//标志访问
 void LCA(int u) {
     pre[u] = u;//构造包含当前点的集合
     visit[u] = true;//标记
     for(int k = head[u]; k != -; k = edge[k].next) {
         if(!visit[edge[k].to]) {
             LCA(edge[k].to);//对未访问的子节点进行LCA
             pre[edge[k].to] = u;//将 一颗子树所在的集合 和 当前集合 合并
         }
     }
     for(int k = qhead[u]; k != -; k = qedge[k].next) {
         if(visit[qedge[k].to]) {//处理查询
             qedge[k].lca = Find(qedge[k].to);
             qedge[k ^ ].lca = qedge[k].lca;
         }
     }
 }

 int main() {
     //输入图
     //相关初始化
         LCA(start);
     return ;
 }