HDU-1402 A * B Problem Plus FFT(快速傅立叶变化)

　　题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=1402

　　一般的的大数乘法都是直接模拟乘法演算过程，复杂度O(n^2)，对于这题来说会超时。乘法的过程基本就是等同于多项式相乘的过程，只是没有进位而已。对于这种问题我们需要转化然后用FFT求解。FFT是用来计算离散傅里叶变化(DFT)及其逆变换(IDFT)的快速算法，复杂度O(n*logn)。DFT有一个很重要的性质：时域卷积，频域乘积；频域乘积，时域卷积。那么什么是时域、频域、卷积、乘积呢？时域和频域是两种信号的分析方法，DFT可以把时域信号变化为频域信号。卷积就是作多项式乘法，乘积就是依次乘过去。如果单纯的用多项式表示法进行乘法运算，那么基本就没有优化的地方了，此时我们换一种多项式的表示方法：点值法。表示的就是n个“点-值”对的序列{(x0,y0),(x1,y1),...,(xn-1,yn-1)}，yk满足yk=A(xk)，A()多项式函数，其中xk的值是随便取的。点值法非常适合作乘法，只需要把对应位置的值乘起来就可以了，复杂度O(n)，其实就是做一次乘积，前面的多项式是做一次卷积。那么我们的重点就是怎样快速的把多项式转换为“点值”表示法，如果单纯的带值进去，那么复杂度就是O(n^2)，这个时候FFT就派上用场了，可以在O(n*logn)的时间内求出来。

　　FFT用到了单位复根的概念，n次单位复根就是满足w^n=1的复数，n次单位复根刚好有n个：e^(2*PI*i*k/n),k=0,1,...,n-1，其中有e^(i*u)=cos(u)+i*sin(u)。n次单位复根有如下的一些引理：

　　　　1.相消引理：对于任何整数n>=0,k>=0,d>0,有 。

　　　　2.折半引理：如果n>0为偶数，n个n次的单位复根的平方等于n/2个n/2次单位复根。公式表示为：。

　　FFT主要是用到了折半引理，对多项式进行分治运算，它用A(x)中偶数下标的系数与奇数下标的系数，分别定义了两个新的次数为n/2的多项式A[0](x)和A[1](x)：

　　　　A[0](x) = a0 + a2x + a4x^4 + ... +an-2x^(n/2-1)
　　　　A[1](x) = a1 + a3x + a5x^4 + ... +an-1x^(n/2-1)

　　那么A(x) = A[0](x^2) + xA[1](x^2)。

　　我们把点值法中x0,x1,...,xn-1的值分别设为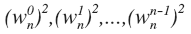，根据折半引理，值的序列并不是由n个不同的值组成的，而是由n/2个n/2次单位复根所组成，每个根出现两次，那么我们就可以对表达式递归的求值了，复杂度O(nlogn)。把多项式用"点值”法表示的问题解决了，然后做一遍乘积就行了。最后就是把“点值”法求的一个向量f求逆就可以了，对应的过程就是IDFT，思想也是差不多的。。。

　　FFT算法，网上模板很好找。。。

 //STATUS:C++_AC_171MS_7128KB
 #include <functional>
 #include <algorithm>
 #include <iostream>
 //#include <ext/rope>
 #include <fstream>
 #include <sstream>
 #include <iomanip>
 #include <numeric>
 #include <cstring>
 #include <cassert>
 #include <cstdio>
 #include <string>
 #include <vector>
 #include <bitset>
 #include <queue>
 #include <stack>
 #include <cmath>
 #include <ctime>
 #include <list>
 #include <set>
 #include <map>
 using namespace std;
 //#pragma comment(linker,"/STACK:102400000,102400000")
 //using namespace __gnu_cxx;
 //define
 #define pii pair<int,int>
 #define mem(a,b) memset(a,b,sizeof(a))
 #define lson l,mid,rt<<1
 #define rson mid+1,r,rt<<1|1
 #define PI acos(-1.0)
 //typedef
 typedef __int64 LL;
 typedef unsigned __int64 ULL;
 //const
 const int N=;
 const int INF=0x3f3f3f3f;
 const int MOD=,STA=;
 const LL LNF=1LL<<;
 const double EPS=1e-;
 const double OO=1e30;
 const int dx[]={-,,,};
 const int dy[]={,,,-};
 const int day[]={,,,,,,,,,,,,};
 //Daily Use ...
 inline int sign(double x){return (x>EPS)-(x<-EPS);}
 template<class T> T gcd(T a,T b){return b?gcd(b,a%b):a;}
 template<class T> T lcm(T a,T b){return a/gcd(a,b)*b;}
 template<class T> inline T lcm(T a,T b,T d){return a/d*b;}
 template<class T> inline T Min(T a,T b){return a<b?a:b;}
 template<class T> inline T Max(T a,T b){return a>b?a:b;}
 template<class T> inline T Min(T a,T b,T c){return min(min(a, b),c);}
 template<class T> inline T Max(T a,T b,T c){return max(max(a, b),c);}
 template<class T> inline T Min(T a,T b,T c,T d){return min(min(a, b),min(c,d));}
 template<class T> inline T Max(T a,T b,T c,T d){return max(max(a, b),max(c,d));}
 //End
 //复数结构体
 struct complex
 {
     double r,i;
     complex(double _r = 0.0,double _i = 0.0)
     {
         r = _r; i = _i;
     }
     complex operator +(const complex &b)
     {
         return complex(r+b.r,i+b.i);
     }
     complex operator -(const complex &b)
     {
         return complex(r-b.r,i-b.i);
     }
     complex operator *(const complex &b)
     {
         return complex(r*b.r-i*b.i,r*b.i+i*b.r);
     }
 };
 /*
  * 进行FFT和IFFT前的反转变换。
  * 位置i和 （i二进制反转后位置）互换
  * len必须去2的幂
  */
 void change(complex y[],int len)
 {
     int i,j,k;
     for(i = , j = len/;i < len-; i++)
     {
         if(i < j)swap(y[i],y[j]);
         //交换互为小标反转的元素，i<j保证交换一次
         //i做正常的+1，j左反转类型的+1,始终保持i和j是反转的
         k = len/;
         while( j >= k)
         {
             j -= k;
             k /= ;
         }
         if(j < k) j += k;
     }
 }
 /*
  * 做FFT
  * len必须为2^k形式，
  * on==1时是DFT，on==-1时是IDFT
  */
 void FFT(complex y[],int len,int on)
 {
     change(y,len);
     for(int h = ; h <= len; h <<= )
     {
         complex wn(cos(-on**PI/h),sin(-on**PI/h));
         for(int j = ;j < len;j+=h)
         {
             complex w(,);
             for(int k = j;k < j+h/;k++)
             {
                 complex u = y[k];
                 complex t = w*y[k+h/];
                 y[k] = u+t;
                 y[k+h/] = u-t;
                 w = w*wn;
             }
         }
     }
     if(on == -)
         for(int i = ;i < len;i++)
             y[i].r /= len;
 }

 char s1[N],s2[N];
 int ans[N];
 complex a[N],b[N];

 int main(){
   //  freopen("in.txt","r",stdin);
     int i,j,len1,len2,len;
     while(~scanf("%s%s",s1,s2))
     {
         len1=strlen(s1);
         len2=strlen(s2);
         len=;
         while(len<(len1<<) || len<(len2<<))len<<=;
         for(i=;i<len1;i++)a[i]=complex(s1[len1-i-]-'',);
         for(;i<len;i++)a[i]=complex(,);
         for(i=;i<len2;i++)b[i]=complex(s2[len2-i-]-'',);
         for(;i<len;i++)b[i]=complex(,);

         FFT(a,len,);
         FFT(b,len,);
         for(i=;i<len;i++)a[i]=a[i]*b[i];
         FFT(a,len,-);
         for(i=;i<len;i++)ans[i]=(int)(a[i].r+0.5);
         len=len1+len2-;
         for(i=;i<len;i++){
             ans[i+]+=ans[i]/;
             ans[i]%=;
         }
         for(i=len;ans[i]<= && i>;i--);
         for(;i>=;i--)
             printf("%d",ans[i]);
         putchar('\n');
     }
     return ;
 }