机器学习经典算法之AdaBoost

一、引言

在数据挖掘中，分类算法可以说是核心算法，其中 AdaBoost 算法与随机森林算法一样都属于分类算法中的集成算法。

/*请尊重作者劳动成果，转载请标明原文链接：*/

/* https://www.cnblogs.com/jpcflyer/p/11268859.html * /

集成的含义就是集思广益，博取众长，当我们做决定的时候，我们先听取多个专家的意见，再做决定。集成算法通常有两种方式，分别是投票选举（bagging）和再学习（boosting）。投票选举的场景类似把专家召集到一个会议桌前，当做一个决定的时候，让 K 个专家（K 个模型）分别进行分类，然后选择出现次数最多的那个类作为最终的分类结果。再学习相当于把 K 个专家（K 个分类器）进行加权融合，形成一个新的超级专家（强分类器），让这个超级专家做判断。

所以你能看出来，投票选举和再学习还是有区别的。Boosting 的含义是提升，它的作用是每一次训练的时候都对上一次的训练进行改进提升，在训练的过程中这 K 个“专家”之间是有依赖性的，当引入第 K 个“专家”（第 K 个分类器）的时候，实际上是对前 K-1 个专家的优化。而 bagging 在做投票选举的时候可以并行计算，也就是 K 个“专家”在做判断的时候是相互独立的，不存在依赖性。

二、 AdaBoost 的工作原理

AdaBoost 的英文全称是 Adaptive Boosting，中文含义是自适应提升算法。它由 Freund 等人于 1995 年提出，是对 Boosting 算法的一种实现。

什么是 Boosting 算法呢？Boosting 算法是集成算法中的一种，同时也是一类算法的总称。这类算法通过训练多个弱分类器，将它们组合成一个强分类器，也就是我们俗话说的“三个臭皮匠，顶个诸葛亮”。为什么要这么做呢？因为臭皮匠好训练，诸葛亮却不好求。因此要打造一个诸葛亮，最好的方式就是训练多个臭皮匠，然后让这些臭皮匠组合起来，这样往往可以得到很好的效果。这就是 Boosting 算法的原理。

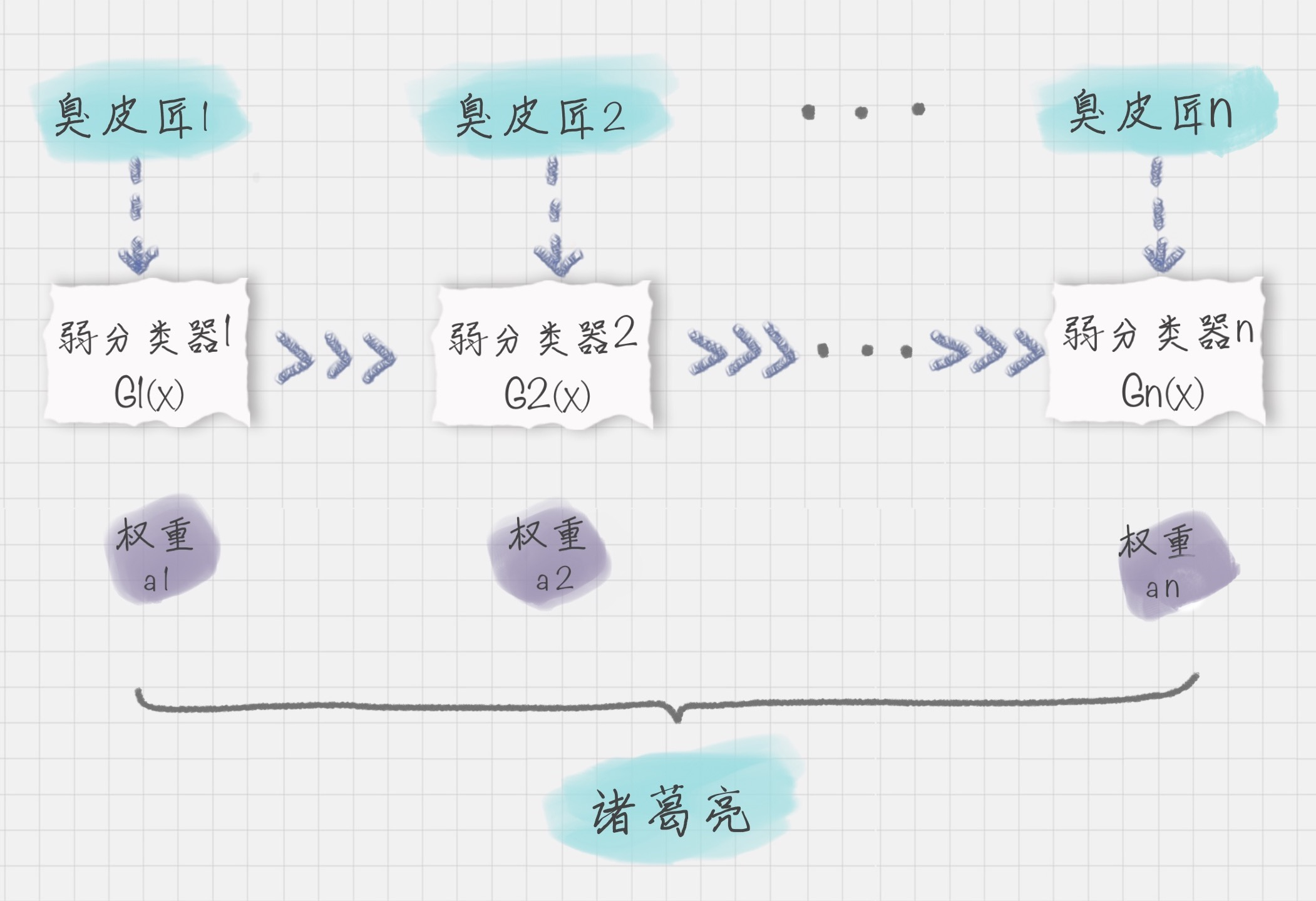
我可以用上面的图来表示最终得到的强分类器，你能看出它是通过一系列的弱分类器根据不同的权重组合而成的。

假设弱分类器为 G_{i}(x) ，它在强分类器中的权重 α_{i} ，那么就可以得出强分类器 f(x)：

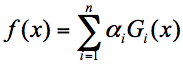
有了这个公式，为了求解强分类器，你会关注两个问题：

1.如何得到弱分类器，也就是在每次迭代训练的过程中，如何得到最优弱分类器？

2.每个弱分类器在强分类器中的权重是如何计算的？

我们先来看下第二个问题。实际上在一个由 K 个弱分类器中组成的强分类器中，如果弱分类器的分类效果好，那么权重应该比较大，如果弱分类器的分类效果一般，权重应该降低。所以我们需要基于这个弱分类器对样本的分类错误率来决定它的权重，用公式表示就是：

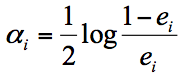
其中 e_{i} 代表第 i 个分类器的分类错误率。

然后我们再来看下第一个问题，如何在每次训练迭代的过程中选择最优的弱分类器？

实际上，AdaBoost 算法是通过改变样本的数据分布来实现的。AdaBoost 会判断每次训练的样本是否正确分类，对于正确分类的样本，降低它的权重，对于被错误分类的样本，增加它的权重。再基于上一次得到的分类准确率，来确定这次训练样本中每个样本的权重。然后将修改过权重的新数据集传递给下一层的分类器进行训练。这样做的好处就是，通过每一轮训练样本的动态权重，可以让训练的焦点集中到难分类的样本上，最终得到的弱分类器的组合更容易得到更高的分类准确率。

我们可以用 D_{k+1} 代表第 k+1 轮训练中，样本的权重集合，其中 W_{k+1,1} 代表第 k+1 轮中第一个样本的权重，以此类推 W_{k+1,N} 代表第 k+1 轮中第 N 个样本的权重，因此用公式表示为：

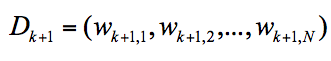
第 k+1 轮中的样本权重，是根据该样本在第 k 轮的权重以及第 k 个分类器的准确率而定，具体的公式为：

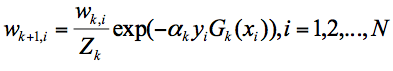
三、 AdaBoost 算法示例

了解 AdaBoost 的工作原理之后，我们看一个例子，假设我有 10 个训练样本，如下所示：

现在我希望通过 AdaBoost 构建一个强分类器。

该怎么做呢？按照上面的 AdaBoost 工作原理，我们来模拟一下。

首先在第一轮训练中，我们得到 10 个样本的权重为 1/10，即初始的 10 个样本权重一致，D1=(0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1, 0.1)。

假设我有 3 个基础分类器：

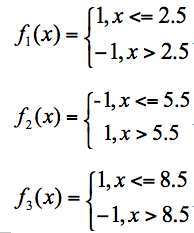
我们可以知道分类器 f1 的错误率为 0.3，也就是 x 取值 6、7、8 时分类错误；分类器 f2 的错误率为 0.4，即 x 取值 0、1、2、9 时分类错误；分类器 f3 的错误率为 0.3，即 x 取值为 3、4、5 时分类错误。

这 3 个分类器中，f1、f3 分类器的错误率最低，因此我们选择 f1 或 f3 作为最优分类器，假设我们选 f1 分类器作为最优分类器，即第一轮训练得到：

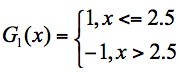
根据分类器权重公式得到：

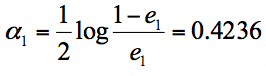
然后我们对下一轮的样本更新求权重值，代入 W_{k+1,i} 和 D_{k+1} 的公式，可以得到新的权重矩阵：D2=(0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.0715, 0.1666, 0.1666, 0.1666, 0.0715)。

在这 3 个分类器中，f3 分类器的错误率最低，因此我们选择 f3 作为第二轮训练的最优分类器，即：

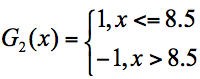
根据分类器权重公式得到：

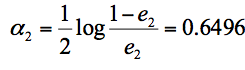
同样，我们对下一轮的样本更新求权重值，代入 W_{k+1,i} 和 D_{k+1} 的公式，可以得到 D3=(0.0455,0.0455,0.0455,0.1667, 0.1667,0.01667,0.1060, 0.1060, 0.1060, 0.0455)。

在第三轮训练中，我们继续统计三个分类器的准确率，可以得到分类器 f1 的错误率为 0.1060*3，也就是 x 取值 6、7、8 时分类错误。分类器 f2 的错误率为 0.0455*4，即 x 取值为 0、1、2、9 时分类错误。分类器 f3 的错误率为 0.1667*3，即 x 取值 3、4、5 时分类错误。

在这 3 个分类器中，f2 分类器的错误率最低，因此我们选择 f2 作为第三轮训练的最优分类器，即：

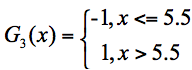
我们根据分类器权重公式得到：

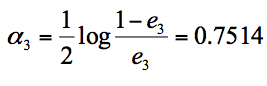
假设我们只进行 3 轮的训练，选择 3 个弱分类器，组合成一个强分类器，那么最终的强分类器 G(x) = 0.4236G1(x) + 0.6496G2(x)+0.7514G3(x)。

实际上 AdaBoost 算法是一个框架，你可以指定任意的分类器，通常我们可以采用 CART 分类器作为弱分类器。通过上面这个示例的运算，你体会一下 AdaBoost 的计算流程即可。

四、 如何使用 AdaBoost 工具

我们可以直接在 sklearn 中使用 AdaBoost。如果我们要用 AdaBoost 进行分类，需要在使用前引用代码：

 from sklearn.ensemble import AdaBoostClassifier

我们之前讲到过，如果你看到了 Classifier 这个类，一般都会对应着 Regressor 类。AdaBoost 也不例外，回归工具包的引用代码如下：

 from sklearn.ensemble import AdaBoostRegressor

我们先看下如何在 sklearn 中创建 AdaBoost 分类器。

我们需要使用 AdaBoostClassifier(base_estimator=None, n_estimators=50, learning_rate=1.0, algorithm=’SAMME.R’, random_state=None) 这个函数，其中有几个比较主要的参数，我分别来讲解下：

1. base_estimator：代表的是弱分类器。在 AdaBoost 的分类器和回归器中都有这个参数，在 AdaBoost 中默认使用的是决策树，一般我们不需要修改这个参数，当然你也可以指定具体的分类器。

2. n_estimators：算法的最大迭代次数，也是分类器的个数，每一次迭代都会引入一个新的弱分类器来增加原有的分类器的组合能力。默认是 50。

3. learning_rate：代表学习率，取值在 0-1 之间，默认是 1.0。如果学习率较小，就需要比较多的迭代次数才能收敛，也就是说学习率和迭代次数是有相关性的。当你调整 learning_rate 的时候，往往也需要调整 n_estimators 这个参数。

4. algorithm：代表我们要采用哪种 boosting 算法，一共有两种选择：SAMME 和 SAMME.R。默认是 SAMME.R。这两者之间的区别在于对弱分类权重的计算方式不同。

5. random_state：代表随机数种子的设置，默认是 None。随机种子是用来控制随机模式的，当随机种子取了一个值，也就确定了一种随机规则，其他人取这个值可以得到同样的结果。如果不设置随机种子，每次得到的随机数也就不同。

那么如何创建 AdaBoost 回归呢？

我们可以使用 AdaBoostRegressor(base_estimator=None, n_estimators=50, learning_rate=1.0, loss=‘linear’, random_state=None) 这个函数。

你能看出来回归和分类的参数基本是一致的，不同点在于回归算法里没有 algorithm 这个参数，但多了一个 loss 参数。

loss 代表损失函数的设置，一共有 3 种选择，分别为 linear、square 和 exponential，它们的含义分别是线性、平方和指数。默认是线性。一般采用线性就可以得到不错的效果。

创建好 AdaBoost 分类器或回归器之后，我们就可以输入训练集对它进行训练。我们使用 fit 函数，传入训练集中的样本特征值 train_X 和结果 train_y，模型会自动拟合。使用 predict 函数进行预测，传入测试集中的样本特征值 test_X，然后就可以得到预测结果。

五、 如何用 AdaBoost 对房价进行预测

了解了 AdaBoost 工具包之后，我们看下 sklearn 中自带的波士顿房价数据集。 这个数据集一共包括了 506 条房屋信息数据，每一条数据都包括了 13 个指标，以及一个房屋价位。

13 个指标的含义，可以参考下面的表格：

这些指标分析得还是挺细的，但实际上，我们不用关心具体的含义，要做的就是如何通过这 13 个指标推导出最终的房价结果。

首先加载数据，将数据分割成训练集和测试集，然后创建 AdaBoost 回归模型，传入训练集数据进行拟合，再传入测试集数据进行预测，就可以得到预测结果。最后将预测的结果与实际结果进行对比，得到两者之间的误差。具体代码如下：

 from sklearn.model_selection import train_test_split

 from sklearn.metrics import mean_squared_error

 from sklearn.datasets import load_boston

 from sklearn.ensemble import AdaBoostRegressor

 # 加载数据

 data=load_boston()

 # 分割数据

 train_x, test_x, train_y, test_y = train_test_split(data.data, data.target, test_size=0.25, random_state=33)

 # 使用 AdaBoost 回归模型

 regressor=AdaBoostRegressor()

 regressor.fit(train_x,train_y)

 pred_y = regressor.predict(test_x)

 mse = mean_squared_error(test_y, pred_y)

 print(" 房价预测结果 ", pred_y)

 print(" 均方误差 = ",round(mse,2))

运行结果：

 房价预测结果  [20.2        10.4137931  14.63820225 17.80322581 24.58931298 21.25076923

 27.52222222 17.8372093  31.79642857 20.86428571 27.87431694 31.09142857

 12.81666667 24.13131313 12.81666667 24.58931298 17.80322581 17.66333333

 27.83       24.58931298 17.66333333 20.90823529 20.10555556 20.90823529

 28.20877193 20.10555556 21.16882129 24.58931298 13.27619048 31.09142857

 17.08095238 26.19217391  9.975      21.03404255 26.74583333 31.09142857

 25.83960396 11.859375   13.38235294 24.58931298 14.97931034 14.46699029

 30.12777778 17.66333333 26.19217391 20.10206186 17.70540541 18.45909091

 26.19217391 20.10555556 17.66333333 33.31025641 14.97931034 17.70540541

 24.64421053 20.90823529 25.83960396 17.08095238 24.58931298 21.43571429

 19.31617647 16.33733333 46.04888889 21.25076923 17.08095238 25.83960396

 24.64421053 11.81470588 17.80322581 27.63636364 23.59731183 17.94444444

 17.66333333 27.7253886  20.21465517 46.04888889 14.97931034  9.975

 17.08095238 24.13131313 21.03404255 13.4        11.859375   26.19214286

 21.25076923 21.03404255 47.11395349 16.33733333 43.21111111 31.65730337

 30.12777778 20.10555556 17.8372093  18.40833333 14.97931034 33.31025641

 24.58931298 22.88813559 18.27179487 17.80322581 14.63820225 21.16882129

 26.91538462 24.64421053 13.05       14.97931034  9.975      26.19217391

 12.81666667 26.19214286 49.46511628 13.27619048 17.70540541 25.83960396

 31.09142857 24.13131313 21.25076923 21.03404255 26.91538462 21.03404255

 21.16882129 17.8372093  12.81666667 21.03404255 21.03404255 17.08095238

 45.16666667]

 均方误差 =  18.05

这个数据集是比较规范的，我们并不需要在数据清洗，数据规范化上花太多精力，代码编写起来比较简单。

同样，我们可以使用不同的回归分析模型分析这个数据集，比如使用决策树回归和 KNN 回归。

编写代码如下：

 # 使用决策树回归模型

 dec_regressor=DecisionTreeRegressor()

 dec_regressor.fit(train_x,train_y)

 pred_y = dec_regressor.predict(test_x)

 mse = mean_squared_error(test_y, pred_y)

 print(" 决策树均方误差 = ",round(mse,2))

 # 使用 KNN 回归模型

 knn_regressor=KNeighborsRegressor()

 knn_regressor.fit(train_x,train_y)

 pred_y = knn_regressor.predict(test_x)

 mse = mean_squared_error(test_y, pred_y)

 print("KNN 均方误差 = ",round(mse,2))

运行结果：

 决策树均方误差 =  23.84

 KNN 均方误差 =  27.87

你能看到相比之下，AdaBoost 的均方误差更小，也就是结果更优。虽然 AdaBoost 使用了弱分类器，但是通过 50 个甚至更多的弱分类器组合起来而形成的强分类器，在很多情况下结果都优于其他算法。因此 AdaBoost 也是常用的分类和回归算法之一。