CF993A Two Squares 几何 第二道 暴力或判断条件（*）

Two Squares

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

You are given two squares, one with sides parallel to the coordinate axes, and another one with sides at 45 degrees to the coordinate axes. Find whether the two squares intersect.

The interior of the square is considered to be part of the square, i.e. if one square is completely inside another, they intersect. If the two squares only share one common point, they are also considered to intersect.

Input

The input data consists of two lines, one for each square, both containing 4 pairs of integers. Each pair represents coordinates of one vertex of the square. Coordinates within each line are either in clockwise or counterclockwise order.

The first line contains the coordinates of the square with sides parallel to the coordinate axes, the second line contains the coordinates of the square at 45 degrees.

All the values are integer and between −100−100 and 100100.

Output

Print "Yes" if squares intersect, otherwise print "No".

You can print each letter in any case (upper or lower).

Examples

input

Copy

0 0 6 0 6 6 0 6
1 3 3 5 5 3 3 1

output

Copy

YES

input

Copy

0 0 6 0 6 6 0 6
7 3 9 5 11 3 9 1

output

Copy

NO

input

Copy

6 0 6 6 0 6 0 0
7 4 4 7 7 10 10 7

output

Copy

YES

Note

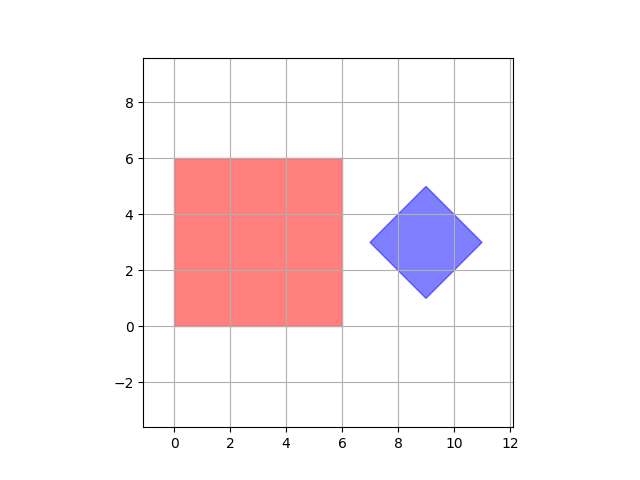
In the first example the second square lies entirely within the first square, so they do intersect.

In the second sample squares do not have any points in common.

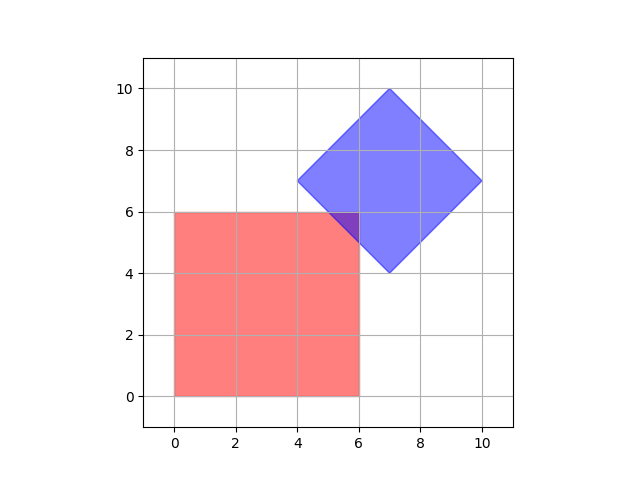
Here are images corresponding to the samples:

题目意思：

给你两个矩形，第一行是一个正面表示的矩形，第二个是一个旋转四十五度角的矩形，问这两个矩形是否相交

因为题目数据范围很小，所以很容易想到的是暴力枚举每个矩形中的每个点，若有点既在第一个矩形又在第二个矩形内则正面两个矩形相交

#include <map>
#include <set>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
#define debug(a) cout << #a << " " << a << endl;
using namespace std;
const int maxn = 1e3 + ;
typedef long long ll;
struct point {
    ll x, y;
};
bool cmp( point p, point q ) {
    if( p.x == q.x ) {
        return p.y < q.y;
    }
    return p.x < q.x;
}
point a[], b[];
ll vis[maxn][maxn];
bool ok() {
    for( ll i = a[].x; i <= a[].x; i ++ ) {
        for( ll j = a[].y; j <= a[].y; j ++ ) {
            vis[i+][j+] = ;
        }
    }
　　//注意枚举第二个矩形的点的时候，循环条件要写明白，不要把矩形外的点枚举进来
    for( ll i = b[].x; i <= b[].x; i ++ ) {
        for( ll j = ; j <= i - b[].x; j ++ ) {
            if( vis[i+][b[].y+j+] || vis[i+][b[].y-j+] ) {
                return true;
            }
        }
    }
    for( ll i = b[].x; i <= b[].x; i ++ ) {
        for( ll j = ; j <= b[].y-b[].y-(i-b[].x); j ++ ) {
            if( vis[i+][b[].y+j+] || vis[i+][b[].y-j+] ) {
                return true;
            }
        }
    }
    return false;
}
int main(){
    std::ios::sync_with_stdio(false);
    while( cin >> a[].x >> a[].y >> a[].x >> a[].y >> a[].x >> a[].y >> a[].x >> a[].y >>
          b[].x >> b[].y >> b[].x >> b[].y >> b[].x >> b[].y >> b[].x >> b[].y ) {
        memset( vis, , sizeof(vis) );
        sort( a + , a + , cmp );
        sort( b + , b + , cmp );
        if( ok() ) {
            cout << "YES" << endl;
        } else {
            cout << "NO" << endl;
        }
    }
    return ;
}

第二种方法是根据两个矩形的相交性质写判断条件，开始自己写的时候想错条件了wa了几发

判断条件是这样的，首先是内含，那只要第二个矩形的点的坐标在第一个矩形的最小和最大之间就满足条件

第二种是两个矩形相交，判断点的坐标之和、坐标之差，只要第一个矩形的坐标之和、坐标之差在第二个矩形的最大最小坐标之和、最大最小坐标之差之间

第三种是两条边刚好有交点，只要第一个矩形的坐标之和、坐标之差在第二个矩形的最大最小坐标之和、最大最小坐标之差的两倍之间

#include <map>
#include <set>
#include <cmath>
#include <queue>
#include <cstdio>
#include <vector>
#include <string>
#include <cstring>
#include <iostream>
#include <algorithm>
#define debug(a) cout << #a << " " << a << endl;
using namespace std;
const int maxn = 1e3 + ;
typedef long long ll;
struct point {
    ll x, y;
};
point a[], b[];
ll vis[maxn][maxn];
bool ok() {

    ll minax = , maxax = -, minay = , maxay = -;
    for( ll i = ; i <= ; i ++ ) {
        minax = min( minax, a[i].x );
        maxax = max( maxax, a[i].x );
        minay = min( minay, a[i].y );
        maxay = max( maxay, a[i].y );
    }
    ll xpymin = , xpymax = -, xmymin = , xmymax = -;
    for( ll i = ; i <= ; i ++ ) {
        xpymin = min( xpymin, b[i].x + b[i].y );
        xpymax = max( xpymax, b[i].x + b[i].y );
        xmymin = min( xmymin, b[i].x - b[i].y );
        xmymax = max( xmymax, b[i].x - b[i].y );
    }
    for( ll i = ; i <= ; i ++ ) {
        ll x = b[i].x, y = b[i].y;
        if( x >= minax && x <= maxax && y >= minay && y <= maxay ) {
            return true;
        }
        ll xpy = a[i].x + a[i].y, xmy = a[i].x - a[i].y;
        if( xpy >= xpymin && xpy <= xpymax && xmy >= xmymin && xmy <= xmymax ) {
            return true;
        }
    }
    ll x = minax + maxax,y = minay + maxay;
    ll xpy = x + y, xmy = x - y;
    if( xpy >= *xpymin && xpy <= *xpymax && xmy >= *xmymin && xmy <= *xmymax ) {
        return true;
    }
    return false;
}
int main(){
    std::ios::sync_with_stdio(false);
    while( cin >> a[].x >> a[].y >> a[].x >> a[].y >> a[].x >> a[].y >> a[].x >> a[].y >>
          b[].x >> b[].y >> b[].x >> b[].y >> b[].x >> b[].y >> b[].x >> b[].y ) {
        memset( vis, , sizeof(vis) );
        if( ok() ) {
            cout << "YES" << endl;
        } else {
            cout << "NO" << endl;
        }
    }
    return ;
}