java递归求八皇后问题解法

八皇后问题

八皇后问题，是一个古老而著名的问题，是回溯算法的典型案例。该问题是国际西洋棋棋手马克斯·贝瑟尔于1848年提出：在8×8格的国际象棋上摆放八个皇后，使其不能互相攻击，即任意两个皇后都不能处于同一行、同一列或同一斜线上，问有多少种摆法。 高斯认为有76种方案。1854年在柏林的象棋杂志上不同的作者发表了40种不同的解，后来有人用图论的方法解出92种结果。

网上有很多八皇后的小游戏，不清楚规则的可以点击这里体验一把。

递归理解

由于我们使用经典的递归回溯算法，所以要先理解递归的调用过程，在使用递归前我们先看下普通方法的调用过程在JVM中如何体现。首先我们来看下jvm中五个重要的空间，如下图所示

这里我们主要关注栈区，当调用某个方法时会在栈区为每个线程分配独立的栈空间,而每个方法都会以栈帧的形式压入栈中，即每个方法从进入到退出都对应着一个栈帧的压栈和出栈。如下图所示

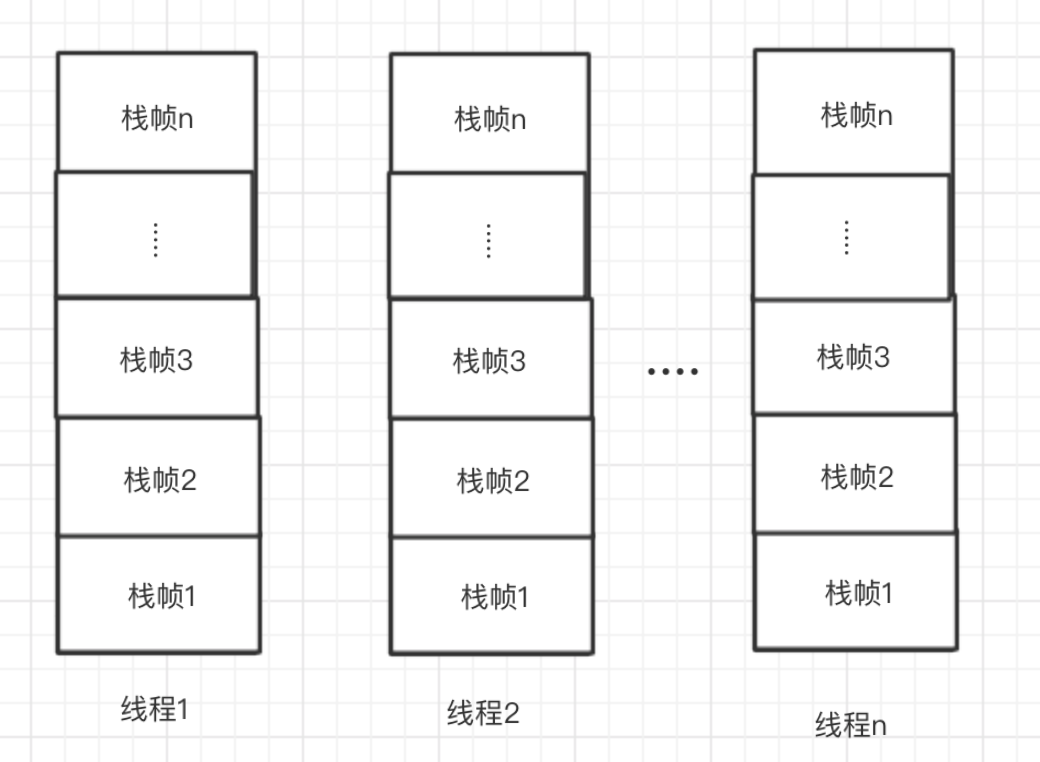
在每个栈帧中都会有方法独立的局部变量表，操作数栈，动态连接，返回地址等信息。如下图所示

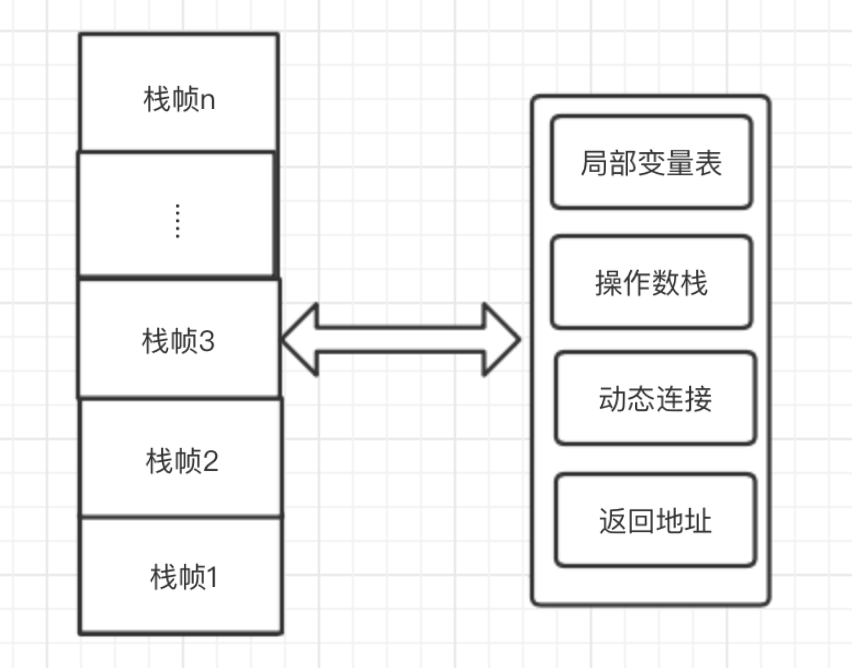
理解了jvm程序栈的结构后，下面我们以图解的方式先讲解一下普通方法(理解普通方法调用过程后，再讲解递归的调用过程)的调用过程。

假设程序main方法首先调用了method1，在method1中调用了method2，在method2中调用method3。代码如下

 public static void main(String []args){
         method1();
     }

     private static void method1(){
         System.out.println("method1调用开始");
         method2();
         System.out.println("method1调用结束");
     }

     private static void method2(){
         System.out.println("method2调用开始");
         method3();
         System.out.println("method2调用结束");
     }
     private static void method3(){
         System.out.println("method3调用开始");
         System.out.println("method3调用结束");
     }

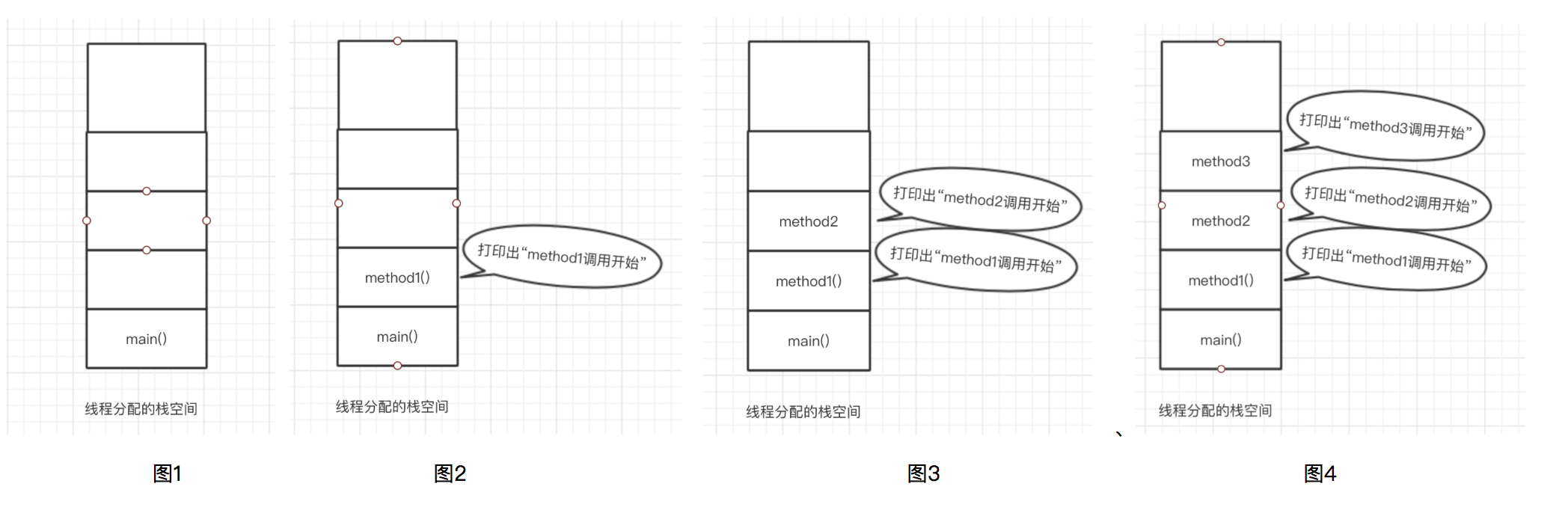
　　当执行main方法时，会执行以下步骤

　　1）首先将main方法压入栈中，在main方法中调用method1，方法mehod1会压入栈中，并执行打印“method1调用开始”

　　2）执行到第7行时，将method2压入栈中，执行method2方法的代码打印出“method2调用开始”

　　3）执行到第13行时调用method3方法，将method3方法压入栈中，执行method3方法打印“method3调用开始”，方法压入栈中的过程图解，如下图所示

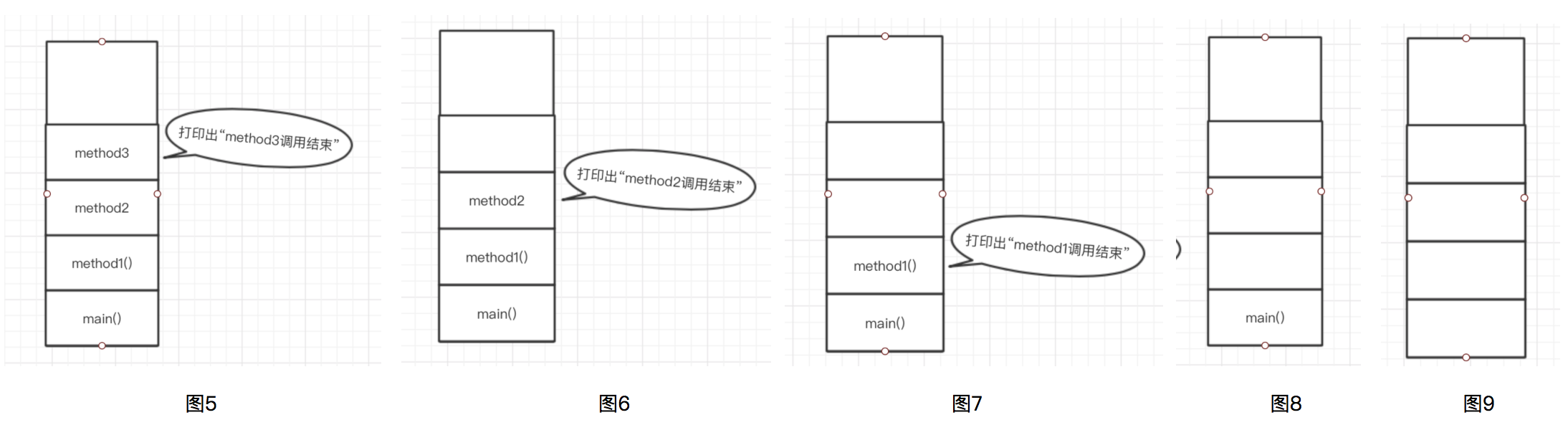
　　当执行到图4中的method3方法打印出“method3调用开始”后会执行以下步骤

　　1）method3执行打印“method3调用结束”后method3方法体已全部执行完毕，method3方法会出栈，并根据栈帧中程序计数器记录的调用者调用本方法的所在行返回。即返回到method2的13行

　　2）执行method2第14行，打印出“method2调用结束”。method2方法体执行完毕，method2方法出栈，返回到method1的第7行

　　3）执行method1第8行，打印出method1调用结束。method1方法出栈，返回到main方法中第2行，main方法执行完毕，main方法出栈，整个程序运行结束

　　对应图解如下

　　根据上面的流程可知程序的运行结果为：

　　method1调用开始

　　method2调用开始

　　method3调用开始

　　method3调用结束

　　method2调用结束

　　method1调用结束

　理解了普通方法的调用过程后，下面我们来讲解递归方法的调用过程，我们都知道递归调用就是方法调用自己，当然我们也可以套用上面普通方法的流程，主观认为它是调用别的方法。

　下面以一个求n的阶乘的递归方法为例讲解调用过程，代码如下

 public static void main(String []args){
         System.out.println(fn(5));
     }

     private static int fn(int n){
         if(n == 1){
             return 1;
         }
         return fn(n-1)*n;
     }

　下面还以图解的方式讲解递归的执行过程，为了好区分每次递归的过程，我们以传入的参数标示fn方法，如n=5时，我们假定调用fn5方法。调用过程如下图所示

　　

　方法的调用扔以压栈的方式进行，调用fn(5)时，fn5压栈，而求fn(5)需要先调用fn(4)，从而fn4压栈，依此类推，直到fn(1)方法压栈，此时if(n==1)条件成立，fn(1)方法返回。如下图

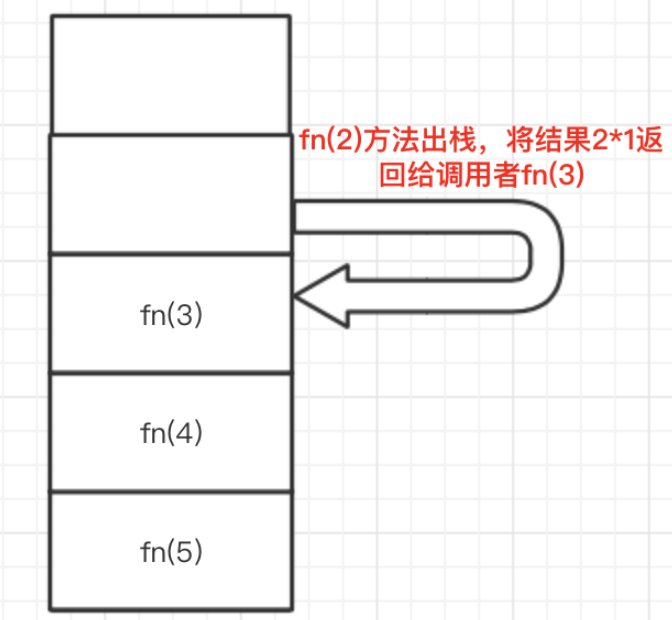
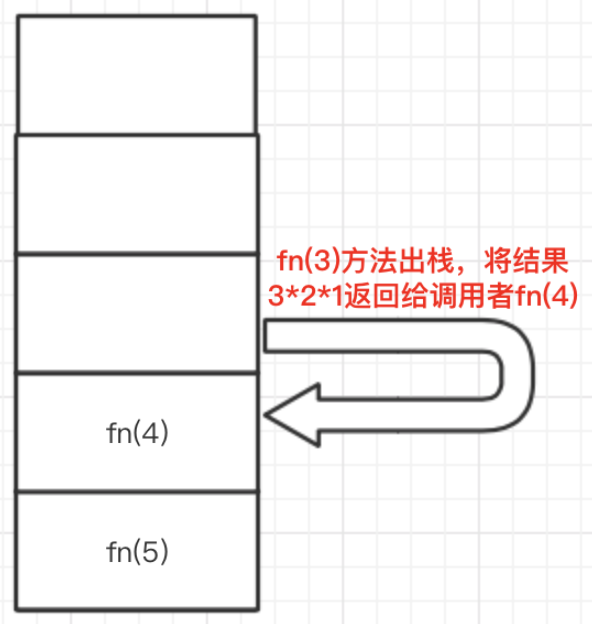
　　　　　　　　图10　　　　　　　　　　　　　　　　　　　　图11　　　　　　　　　　　　　　　图12　　　　　　　　　　　　　　　　　　图13

　

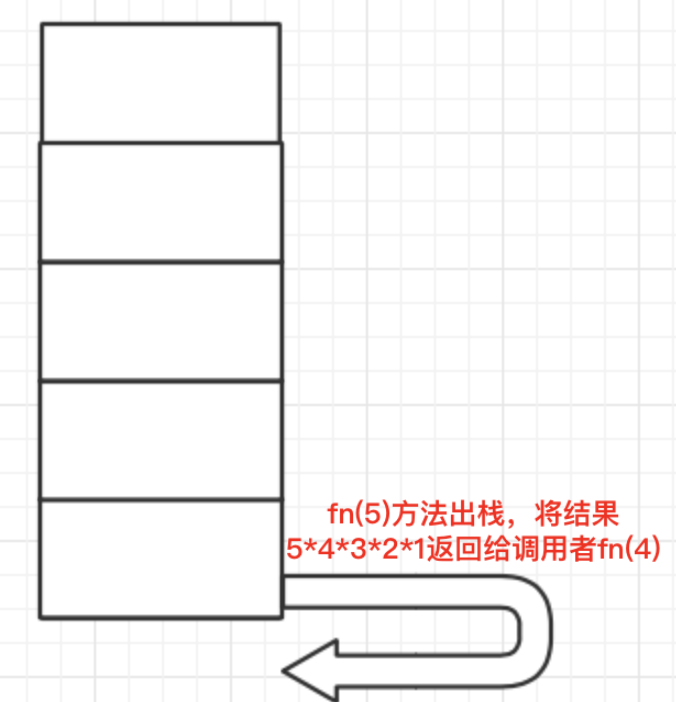
　　　　　　　　图14

　　执行到图14后，递归的执行过程结束，并将结果5*4*3*2*1的结果返回给main方法并输出，结果为120。

　　以上就是递归的执行过程分析，其实跟普通方法的调用过程一样，只不过递归调用的方法是自己而已。

　　好了，终于到了本文的重点了(铺垫做的太多)，递归回溯法求八皇后解法问题

八皇后问题解法

　　问题分析

　　1）用代码求解八皇后问题的前提，我们要先构造出来一个8*8的二维数组，但由于八皇后问题的条件限制----任意两个皇后不能同行，所以我们可使用一个8位一维数组表示棋盘，一维数组的第n个元素即代表第n-1(从第0行开始)行，第n个元素的值即代表第n行的列值，如：0 4 7 5 2 6 1 3 ，其中0表示第0行第0列，4表示第2行第5列，7表示第3行第8列，以此类推。

　　2）我们在求解的过程中，每添加一个皇后，行数加1，所以不会出现任意两个皇后处在同一行的情况，所以我们只需判断任意两个皇后不在同一列，也不在同一斜线上即可。

　　3）从第0行第0列开始放第一个皇后，依此循环8个皇后，并在下一行判断，只要不跟前面所有皇后在同一列或同一斜线上即可放置皇后。

　　代码实现

 /**
  * 递归法解决八皇后问题
  */
 public class BaHuangHou {
     private final static int max = 8;
     private static int array[] = new int[max];
     private static int count = 0;
     public static void main(String []args){
         //定义一个一位数组表示八皇后的棋盘(第n个代表第n行，值代表第n行的第m列)

         check(0);
         System.out.printf("总共有%d种解法\n",count);
     }

     /**
      * 放置第n个皇后
      * @param n
      * @return
      */
     private static void check(int n){
         if(n == max){
             print(array);
             return;
         }
         for(int i=0; i<max; i++){
             array[n] = i;
             if(judge(n)){
                 check(n+1);
             }
         }
     }
     /**
      * 判断第n个皇后是否与之前的冲突
      * @param n
      * @return
      */
     private static boolean judge(int n){
         for(int i=0; i<n; i++){
             if(array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i])){
                 return false;
             }
         }
         return true;
     }

     /**
      * 打印数组值
      * @param array
      */
     public static void print(int array[]){
         for (int i = 0; i <max; i++) {
             System.out.print(array[i]+" ");
         }
         count ++ ;
         System.out.println();

     }
 }

　　代码分析

　　首先我们定义了一个8个元素的一维数组 array ，用来表示一个8*8的棋盘。

　　1）先来看下判断皇后是否与前面冲突(即在同一列或同一斜线)的judge方法：

　　　　if(array[i] == array[n] || Math.abs(n-i) == Math.abs(array[n] - array[i]))

　　　　第一个条件array[i] == array[n]，因一维数组的值即代表所在行的所在列值，所以如果值相同，则代表在同一列。

　　　　第二个条件Math.abs(n-i) == Math.abs(array[n] - array[i])，n-i表示两个皇后相差几行，array[n]-array[i]表示相差几列，如果相差行等于相差，则这两个皇后能构成一个正方形，即在同一斜线上。

　　2）在来看执行判断过程的check方法：

 private static void check(int n){
         if(n == max){
             print(array);
             return;
         }
         for(int i=0; i<max; i++){
             array[n] = i;
             if(judge(n)){
                 check(n+1);
             }
         }
     }

　　第2行的if()条件判断，用于表示一次求解过程的结束。当n==max即n=8时，即表示前面已经放置了8个皇后（n从0开始）。

　　第6行的for循环，表示从第0行的第0列开始放第一个皇后，一直到第0行的第7列遍历出所有第0行的皇后摆放方法。同理，执行到n=1时，表示放置第二个皇后，即第2行的摆放方法，只要第二行不跟第一行冲突，就在第三行放置第3个皇后，以此类推直到放置第7行的第八个皇后。如果在某行遍历完所在行的所有列，均与前面的皇后冲突，说明前面的摆放不能求解出一个八皇后解法，此时该行的循环执行结束，该行所在的方法出栈，回溯到前面一行的方法执行。前面一行继续执行for循环的i++，当i++后即该行皇后向后一个位置移动，如果不跟前面的所有皇后冲突，则再进入下一行的下一个皇后从第0列开始摆放，依此类推。

　　当得到一个正确解法后，n=8所在方法出栈(参考前面讲解的递归方法入栈出栈)，执行n=7（第8个皇后）所在方法的for循环，继续执行i++，查看最后一行的皇后后面列是否还有正确解法，如果有则输出，如果没有则该行所在方法出栈，进而执行n=6（第7个皇后）所在方法的for循环，继续执行i++。依此类推

　　用文字描述稍微有点抽象，不过如果理解了我们前面讲解的递归方法的执行过程，理解起来还是比较容易的。这里使用了for循环求解八皇后的所有解法，所以相对会难以理解。

　图解的方式理解八皇后解法（虚线圆表示不能摆放，用实线圆形表示可以摆放）

　　在main方法中调用check(0)后，n=0的check方法入栈，并执行for循环的i=0，array[0]=0，即第一个皇后摆放在第0行第0列，此时程序栈和棋盘情况如下图所示　　

　　

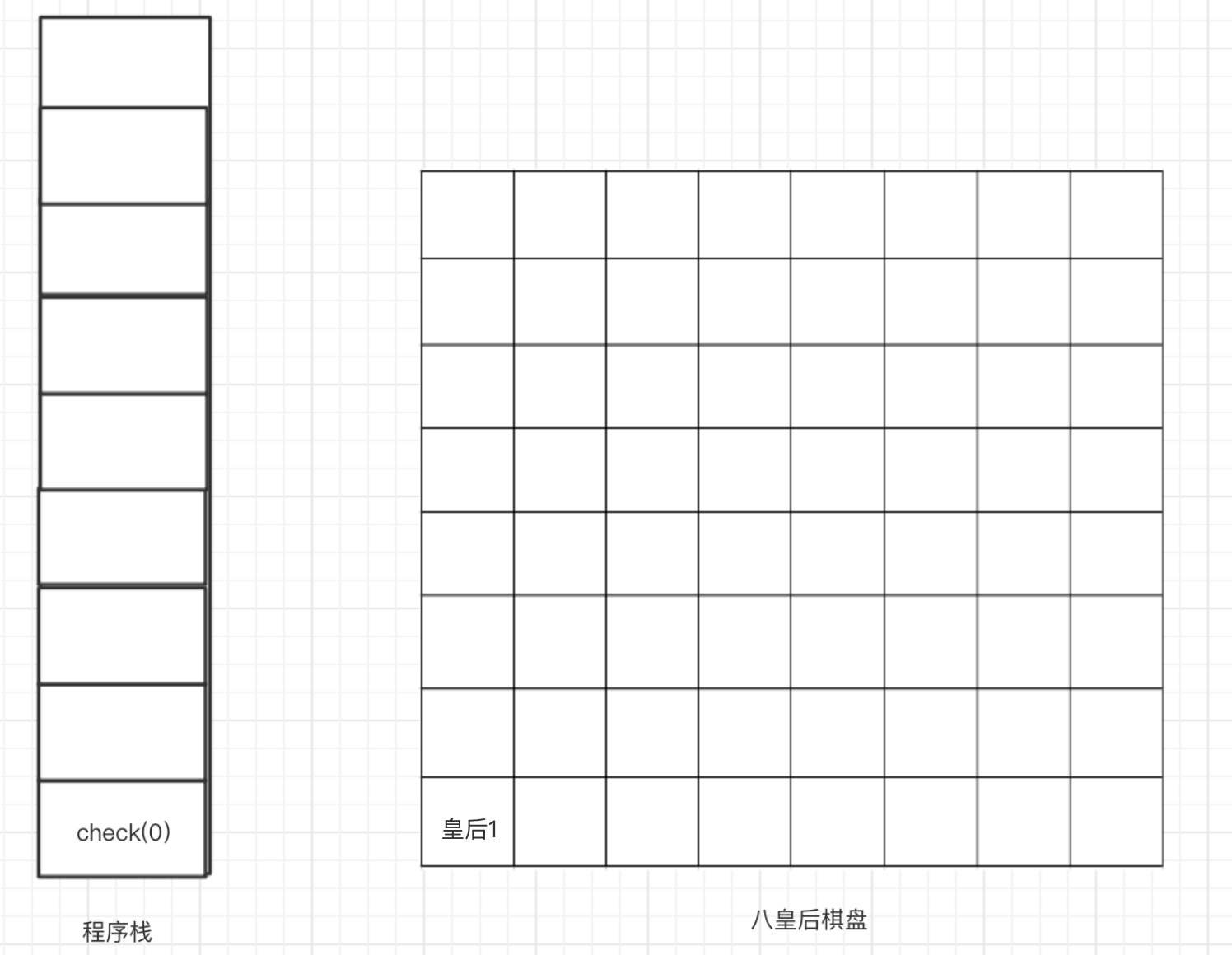
　　由于这时是第一个皇后，所以肯定没有冲突，但要记住n=0时的check方法的for循环只进行到i=0，便调用check(1)，调用下一个皇后的摆放判断，此时程序栈和棋盘情况如下图所示

　　

　　当n=1的check方法入栈后，执行for循环方法，由于i=0和i=1均会与第一个皇后冲突，所以这两个位置不能摆放，此时n=1的check方法的for循环执行到i=2。第二个皇后摆放后，会调用check(2)，则n=2的check方法入栈，此时程序栈和棋盘情况如下图所示

　　

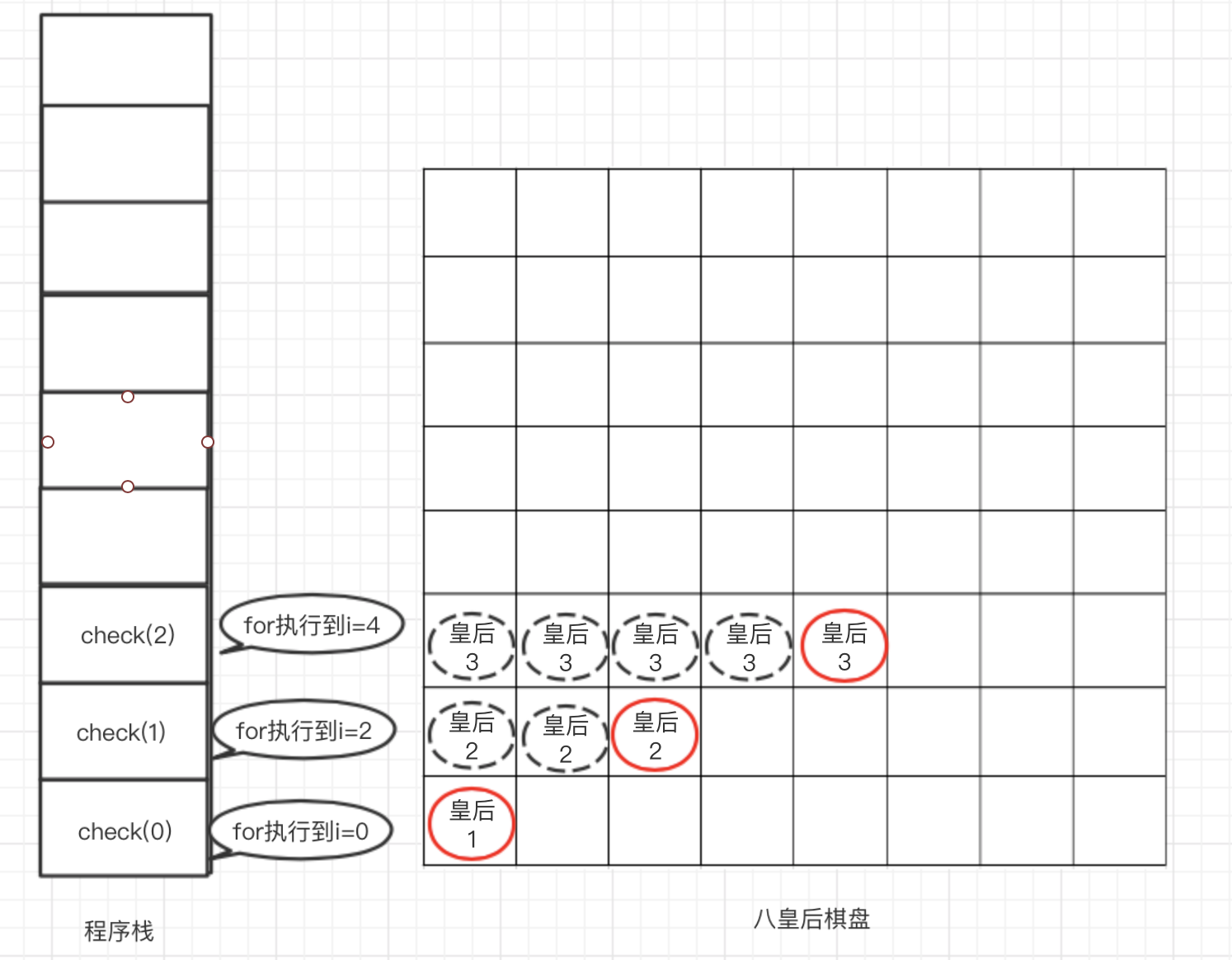
　　第n=2的check方法入栈后，执行for循环方法，在i<4之前的所有位置均会与前面两个皇后冲突，所以只能放在i=4的位置。此时n=2的check方法的for循环执行到i=4。调用check(3)，则n=3的check方法入栈，此时程序栈和期盼情况如下图所示

　　

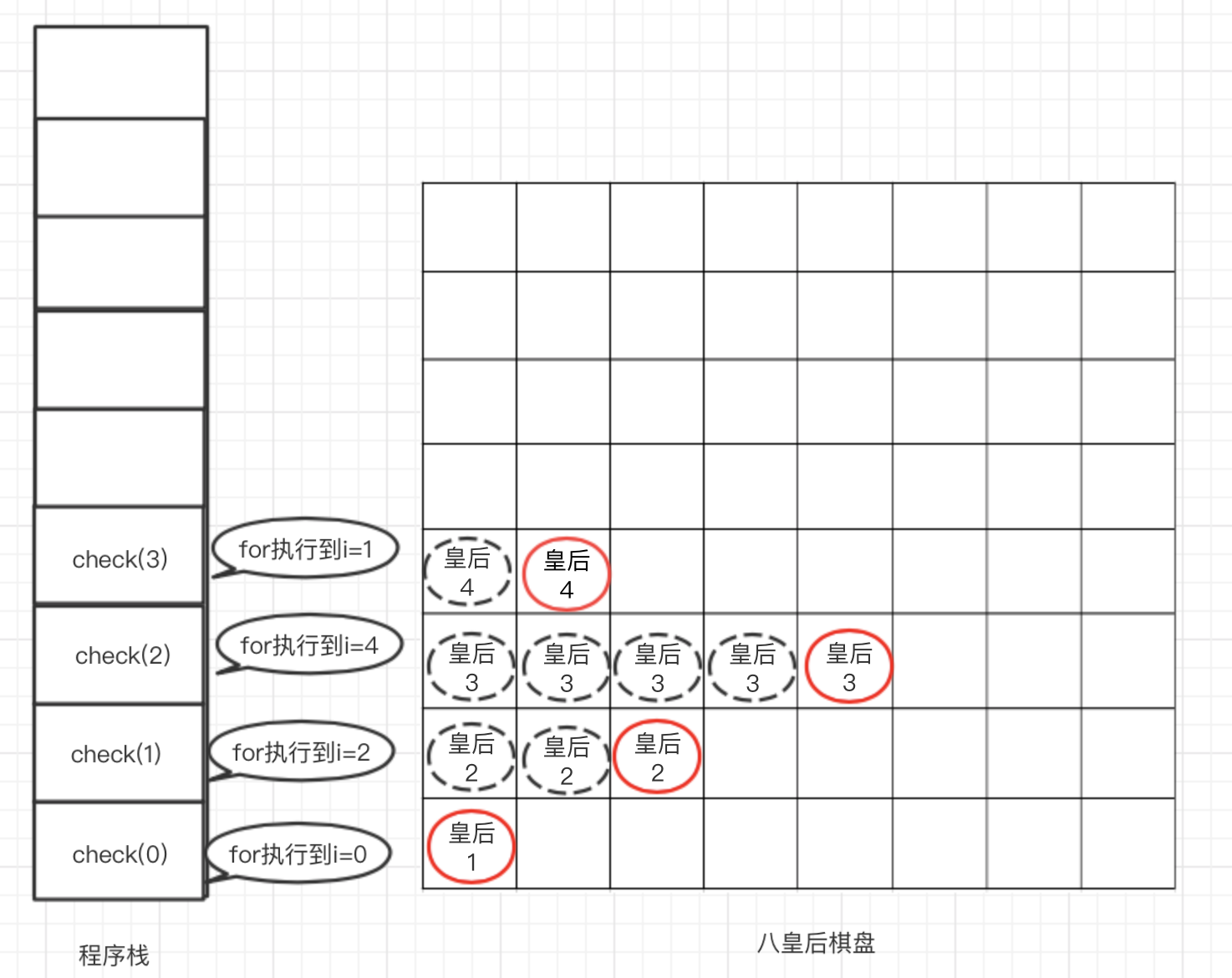
　　n=3的所在行摆放皇后之后，调用check(4)的方法，此时n=2的check方法的for循环执行到i=4。

　　依此类推，直到执行到n=5时，for循环执行完所有遍历，发现均与前面的皇后冲突，如下图所示

　　

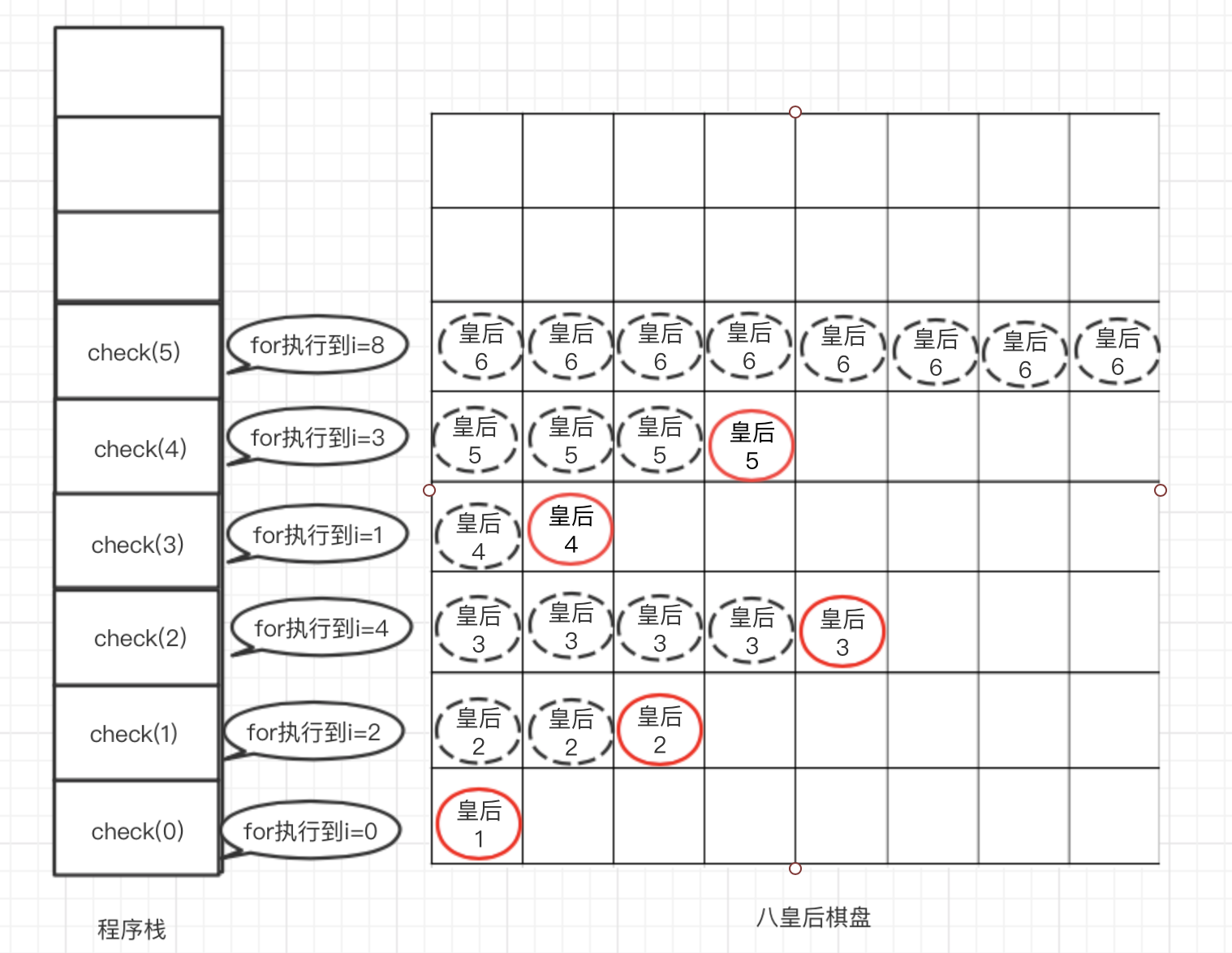
　　当n=5的for循环执行完后，check(5)方法出栈，回溯到check(4)的方法继续执行for循环，前面我们知道check(4)的for循环i执行到i=3，所以从i=3继续执行i++，如下图所示

　　

　　可以看出n=4的check方法执行到i=7时，才能满足不与前面的皇后冲突，这时会继续调用check(5)方法，即n=5的check方法再次入栈，如下图所示

　　

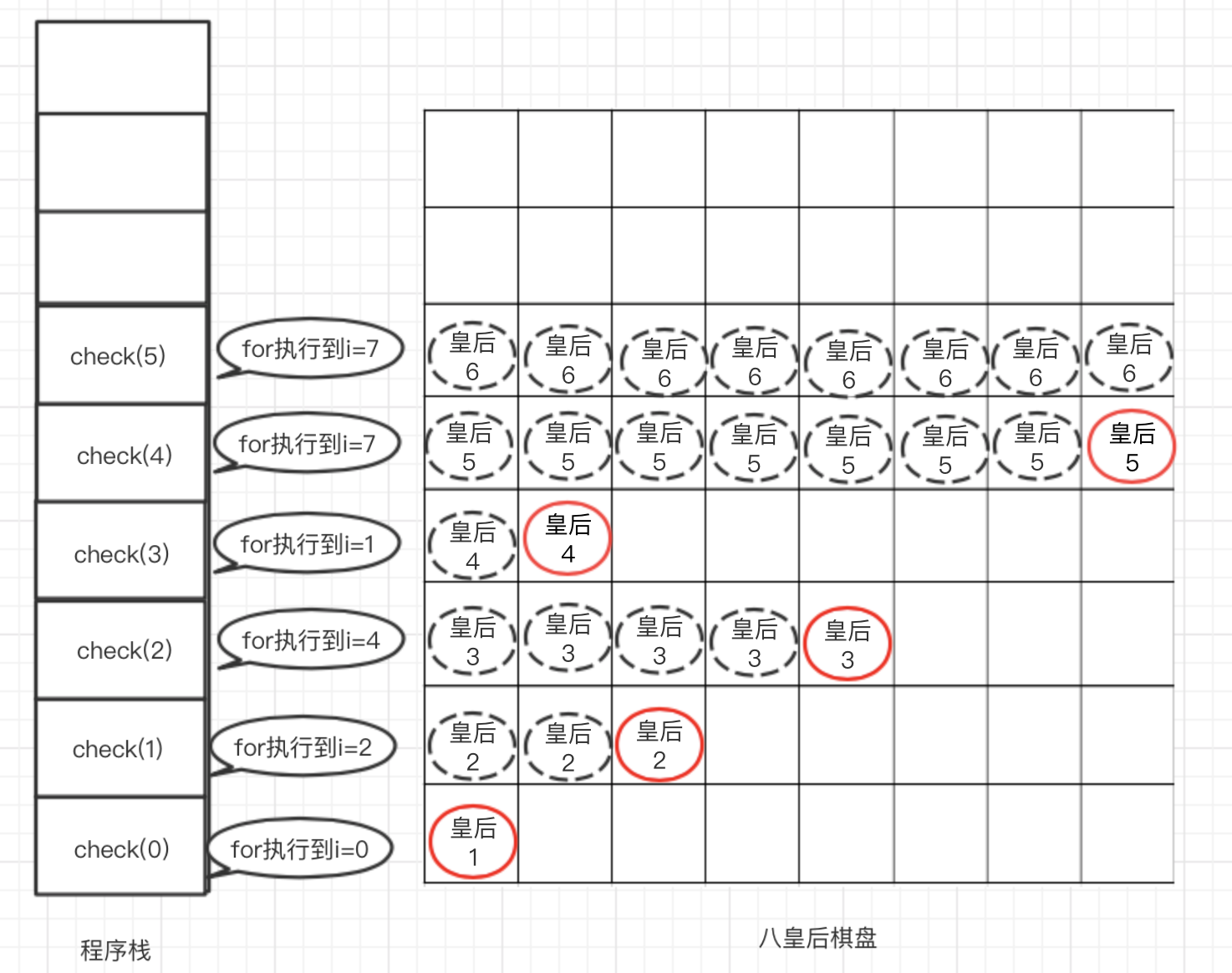
　　可以看出n=5时，所在行的所有列均无法摆放皇后，所示n=5的check方法再次出栈，而n=4的check方法的for循环也执行到i=7，所以check(4)方法也会出栈，进而执行n=3的for循环，而我们之前记录可以看到n=3的for循环执行到i=1，所以继续执行i++，并依此判断是否与前面的皇后冲突。

　　从上面的过程我们可以看到，当栈顶方法所在行的所有列均不能摆放皇后时，会回溯到前面的行执行。

　　下面我们在用一个摆放成功的案例来讲解回溯过程，例如，0 4 7 5 2 6 1 3  即(0,0) (1,4) (2,7) (3,5) (4,2) (5,6) (7,1) (8,3)的摆法，此时程序栈和棋盘如下图所示

　　

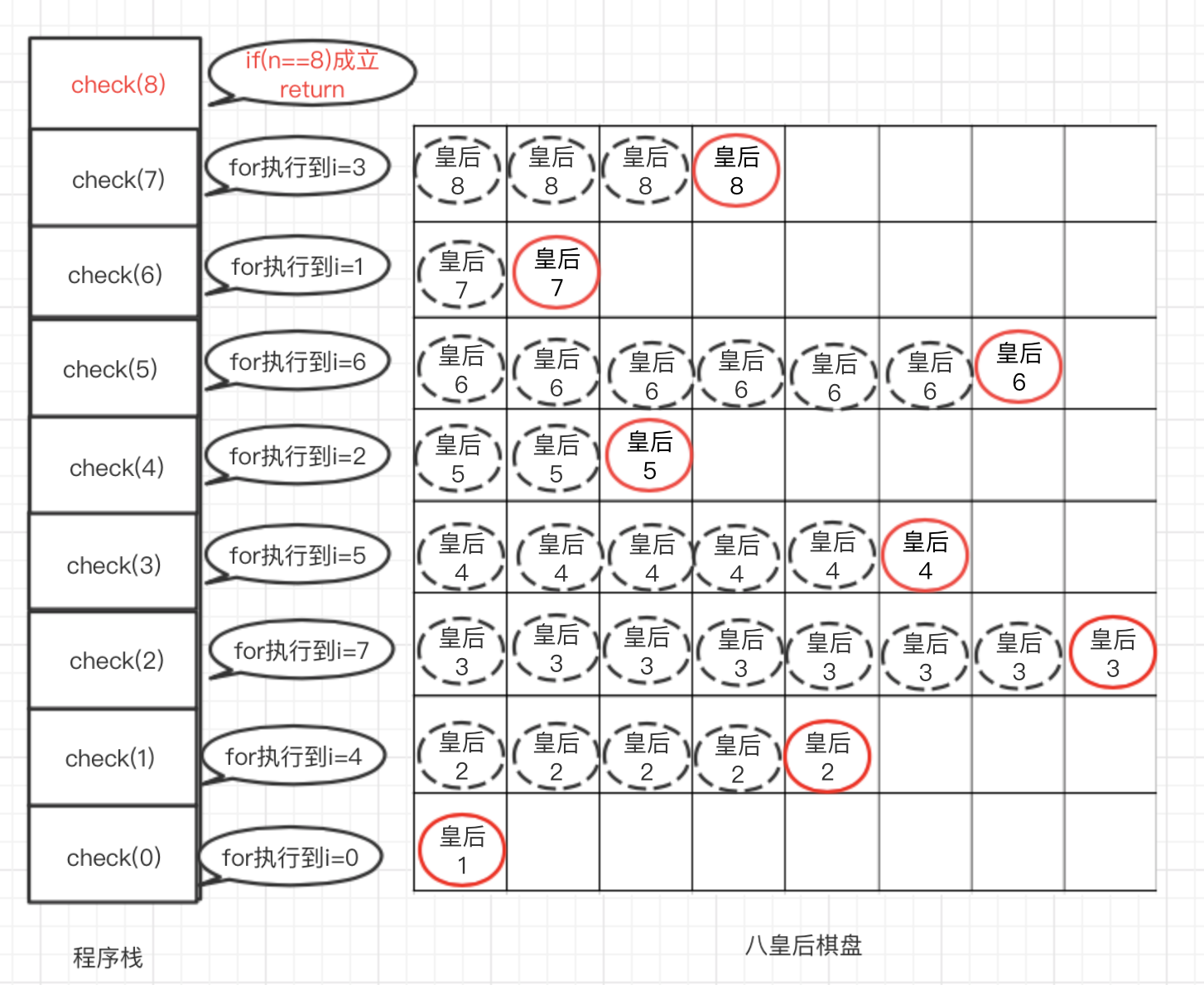
　　可以看到，n=7时第八个皇后摆放成功，会调用check(8)，进而满足if(n==8)条件，所以check(8)方法出栈，继续执行n=7的check方法，而此时n=7的for循环i=3，继续执行i++，看n=7的所在行的后面的列是否还有能摆放成功的。如果没有则n=7的check方法执行完毕，回溯到n=6的方法，依此类推，知道所有的八皇后解法全部求出。

总结

　　好了，到这里不知道大家是否理解了使用递归回溯法求八皇后解法的问题？如有疑问的地方，可以在留言区评论提问。